【队列】力扣23:合并K个升序链表()
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
先来看一个更简单的问题:如何合并两个有序链表?假设链表 a 和 b 的长度都是 n,如何在 O(n) 的时间代价以及 O(1) 的空间代价完成合并?
为了达到空间代价是 O(1),宗旨是【原地调整链表元素的 next 指针】完成合并。
- 首先需要一个变量 head 来保存【合并之后链表的头部】,可以把 head 设置为一个虚拟的头(也就是 head 的 val 属性不保存任何值),这是为了方便代码的书写,在整个链表合并完之后,返回它的下一位置即可。
- 需要一个指针 tail 来记录【下一个插入位置的前一个位置】,以及两个指针 aPtr 和 bPtr 来记录 a 和 b 【未合并部分的第一位】。注意这里的描述,tail 不是下一个插入的位置,aPtr 和 bPtr 所指向的元素处于「待合并」的状态,也就是说它们还没有合并入最终的链表。当然,也可以给他们赋予其他定义,定义不同实现就会不同。
- 当 aPtr 和 bPtr 都不为空的时候,取 val 实现较小的合并;如果 aPtr 为空,则把整个 bPtr 以及后面的元素全部合并;当 bPtr 为空时同理。
- 在合并的时候,应该先调整 tail 的 next 属性,再后移 tail 和 *Ptr(aPtr 或 bPtr)。那么这里 tail 和 *Ptr 是否存在先后顺序呢?它们谁先动谁后动都是一样的,不会改变任何元素的 next 指针。
@ C++
ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
if ((!a) || (!b)) return a ? a : b;
ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
while (aPtr && bPtr) {
if (aPtr->val < bPtr->val) {
tail->next = aPtr; aPtr = aPtr->next;
} else {
tail->next = bPtr; bPtr = bPtr->next;
}
tail = tail->next;
}
tail->next = (aPtr ? aPtr : bPtr);
return head.next;
}
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/merge-k-sorted-lists/solution/he-bing-kge-pai-xu-lian-biao-by-leetcode-solutio-2/
时间复杂度:O(n)。
空间复杂度:O(1)。
方法1:顺序合并
一种最朴素的方法:用一个变量 ans 来维护以及合并的链表,第 i 次循环把第 i 个链表和 ans 合并,答案保存到 ans 中。
@ C++
class Solution {
public:
ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
if ((!a) || (!b)) return a ? a : b;
ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
while (aPtr && bPtr) {
if (aPtr->val < bPtr->val) {
tail->next = aPtr; aPtr = aPtr->next;
} else {
tail->next = bPtr; bPtr = bPtr->next;
}
tail = tail->next;
}
tail->next = (aPtr ? aPtr : bPtr);
return head.next;
}
ListNode* mergeKLists(vector<ListNode*>& lists) {
ListNode *ans = nullptr;
for (size_t i = 0; i < lists.size(); ++i) {
ans = mergeTwoLists(ans, lists[i]);
}
return ans;
}
};
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/merge-k-sorted-lists/solution/he-bing-kge-pai-xu-lian-biao-by-leetcode-solutio-2/
时间复杂度:假设每个链表的最长长度是 n。在第一次合并后,ans 的长度为 n;第二次合并后,ans 的长度为 2×n,第 i 次合并后,ans 的长度为 i×n。第 ii 次合并的时间代价是 O(n+(i−1)×n)=O(i×n),那么总的时间代价为 O(∑k (i×n))=O((1+k)⋅k/2 × n)=O(k^2·n),故渐进时间复杂度为 O(k^2·n)。
空间复杂度:没有用到与 k 和 n 规模相关的辅助空间,故渐进空间复杂度为 O(1)。
方法2:分治合并
考虑优化方法1,用分治的方法进行合并。
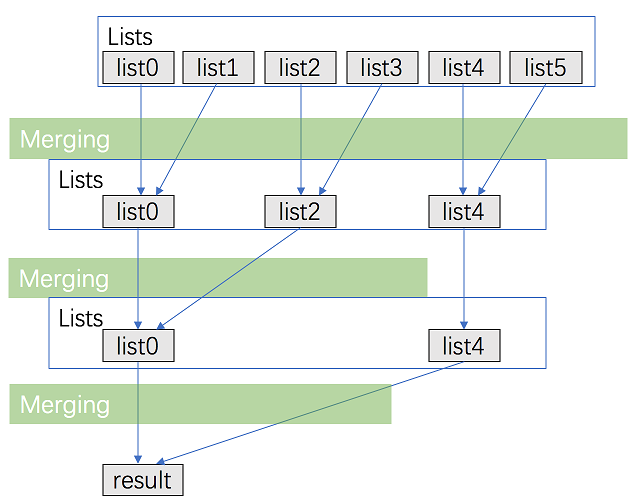
- 将 k 个链表配对并将同一对中的链表合并;第一轮合并以后, k 个链表被合并成了 k/2 个链表,平均长度为 2n/k ,然后是 k/4 个链表,k/8 个链表等等;
- 重复这一过程,直到得到最终的有序链表。
![image]()
@ C++
class Solution {
public:
ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
if ((!a) || (!b)) return a ? a : b;
ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
while (aPtr && bPtr) {
if (aPtr->val < bPtr->val) {
tail->next = aPtr; aPtr = aPtr->next;
} else {
tail->next = bPtr; bPtr = bPtr->next;
}
tail = tail->next;
}
tail->next = (aPtr ? aPtr : bPtr);
return head.next;
}
ListNode* merge(vector <ListNode*> &lists, int l, int r) {
if (l == r) return lists[l];
if (l > r) return nullptr;
int mid = (l + r) >> 1;
return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
}
ListNode* mergeKLists(vector<ListNode*>& lists) {
return merge(lists, 0, lists.size() - 1);
}
};
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/merge-k-sorted-lists/solution/he-bing-kge-pai-xu-lian-biao-by-leetcode-solutio-2/
时间复杂度:考虑递归「向上回升」的过程——第一轮合并 k/2 组链表,每一组的时间代价是 O(2n);第二轮合并 k/4 组链表,每一组的时间代价是 O(4n)…… 所以总的时间代价是 O(∑∞ k/(2^t × 2^i · n) = O(kn×logk),故渐进时间复杂度为 O(kn×logk)。
空间复杂度:递归会使用到 O(logk) 空间代价的栈空间。
@ python
# 每次从列表中弹出两个链表,升序后添加到列表末尾,直到列表中只剩一个链表
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution(object):
#合并两个升序链表
def mergeTwoList(self,head1,head2):
head = ListNode(-1)
p = head
while head1 and head2:
if head1.val<=head2.val:
p.next = head1
head1 = head1.next
else:
p.next = head2
head2 = head2.next
p = p.next
p.next = head1 if head1 else head2
return head.next
def mergeKLists(self, lists):
"""
:type lists: List[ListNode]
:rtype: ListNode
"""
if not lists:
return None
if len(lists)<2:
return lists[0]
while len(lists)>=2:
lists.insert(0,self.mergeTwoList(lists.pop(),lists.pop()))
return lists[0]
方法3:优先队列
需要维护当前每个链表没有被合并的元素的最前面一个,k 个链表就最多有 k 个满足这样条件的元素,每次在这些元素里面选取 val 属性最小的元素合并到答案中。
在选取最小元素的时候,可以用优先队列来优化这个过程:
把所有的链表存储在一个优先队列中,每次提取所有链表头部节点值最小的那个节点,直到所有链表都被提取完为止。注意 Comp 函数默认是对最大堆进行比较并维持递增关系,如果想要获取最小的节点值,则需要实现一个最小堆,因此比较函数应该维持递减关系。
- 新建小顶堆,小顶堆的大小是 k,不断从每个链表的头节点开始不断加入小顶堆中,然后取出堆顶值,也就是最小值,然后继续往小顶堆中插入这个最小值在链表的 next 节点。
优先队列(priority queue)可以在 O(1) 时间内获得最大值,并且可以在 O(log n) 时间内取出最大值或插入任意值。常用堆(heap)来实现。
堆是一个完全二叉树,其每个节点的值总是大于等于子节点的值。实际实现堆时,通常用一个数组而不是用指针建立一个树。这是因为堆是完全二叉树,所以用数组表示时,位置 i 的节点的父节点位置一定为 i/2,而它的两个子节点的位置又一定分别为 2i 和 2i+1。
class Solution:
def mergeKLists(self, lists: List[ListNode]) -> ListNode:
import heapq
dummy = ListNode(0)
p = dummy
head = []
for i in range(len(lists)):
if lists[i] :
heapq.heappush(head, (lists[i].val, i))
lists[i] = lists[i].next
while head:
val, idx = heapq.heappop(head)
p.next = ListNode(val)
p = p.next
if lists[idx]:
heapq.heappush(head, (lists[idx].val, idx))
lists[idx] = lists[idx].next
return dummy.next
作者:powcai
链接:https://leetcode.cn/problems/merge-k-sorted-lists/solution/leetcode-23-he-bing-kge-pai-xu-lian-biao-by-powcai/
时间复杂度:O(nk∗log(k)),n 是所有链表中元素的总和,k 是链表个数。考虑优先队列中的元素不超过 k 个,那么插入和删除的时间代价为O(logk),这里最多有 kn 个点,对于每个点都被插入删除各一次,故总的时间代价即渐进时间复杂度为 O(kn×logk)。
空间复杂度:这里用了优先队列,优先队列中的元素不超过 k 个,故渐进空间复杂度为 O(k)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号