激活函数

常见的激活函数有 sigmoid 、tanh 和 relu 三种非线性函数，数学表达式分别为：
sigmoid：$ y = \frac{1}{1 + e^{-x}} $

tanh：\(y = \frac{e^x - e^{-x}}{e^x + e^{-x}}\)

relu：$ y = max(0, x) $

Pyhton代码：

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

def relu(x):
    return np.maximum(0, x)

x = np.arange(-5, 5, 0.1)

p1 = plt.subplot(311)
y = tanh(x)
p1.plot(x, y)
p1.set_title('tanh')
p1.axhline(ls='--', color='r')
p1.axvline(ls='--', color='r')

p2 = plt.subplot(312)
y = sigmoid(x)
p2.plot(x, y)
p2.set_title('sigmoid')
p2.axhline(0.5, ls='--', color='r')
p2.axvline(ls='--', color='r')

p3 = plt.subplot(313)
y = relu(x)
p3.plot(x, y)
p3.set_title('relu')
p3.axvline(ls='--', color='r')

plt.subplots_adjust(hspace=1)
plt.show()

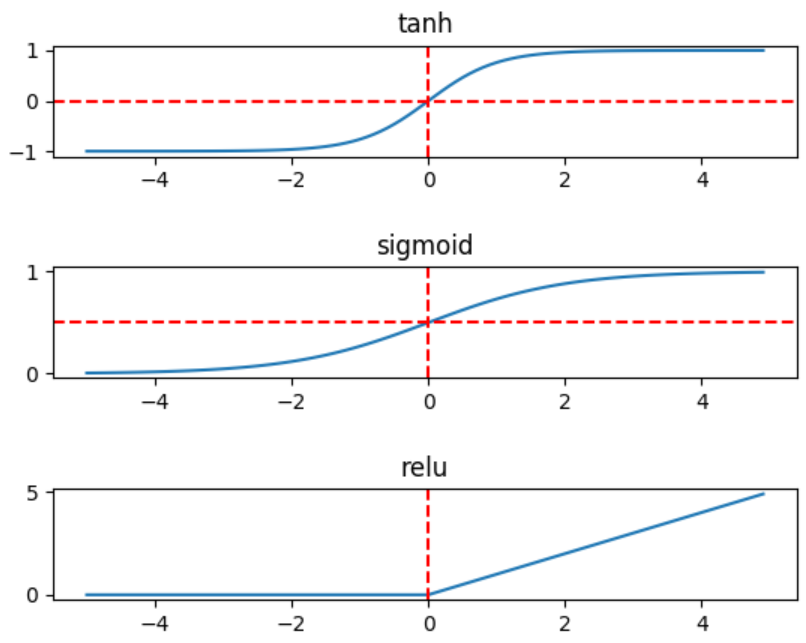
相较而言，在隐藏层，tanh函数要优于sigmoid函数，可以认为tanh是sigmoid的平移版本，优势在于其取值范围介于-1 ~ 1之间，数据的平均值为0，而不像sigmoid为0.5，有类似数据中心化的效果。

但在输出层，sigmoid也许会优于tanh函数，原因在于你希望输出结果的概率落在 0 ~ 1 之间，比如二元分类，sigmoid可作为输出层的激活函数。

但实际应用中，特别是深层网络在训练时，tanh 和 sigmoid 会在端值趋于饱和，造成训练速度减慢，故深层网络的激活函数默认大多采用relu函数，浅层网络可以采用 sigmoid 和 tanh 函数。

激活函数的求导公式

有必要了解激活函数的求导公式，在反向传播中才知道是如何进行梯度下降。

相关基础求导公式

\((x^n)' = n * x^{n-1}\)
\((e^x)' = e^x\)
\((\frac{u}{v})' = \frac{u' v - u v'}{v^2}\)

1、sigmoid求导函数

$ y = \frac{1}{1 + e^{-x}} $ 即 \(y = (1 + e^{-x})^{-1}\)
应用微积分的链式法则，其求导过程为：

\[ \begin{align*} \frac{dy}{dx} &= [(1 + e^{-x})^{-1}]'\\ &= (-1) * (1 + e^{-x})^{-2} * e^{-x} * (-1)\\ &= (1 + e^{-x})^{-2} * e^{-x}\\ &= \frac{e^{-x}}{(1 + e^{-x})^{-2}}\\ &= \frac{(1 + e^{-x}) - 1}{(1 + e^{-x})^{-2}}\\ &= (1 + e^{-x})^{-1} - (1 + e^{-x})^{-2}\\ &= y - y ^ 2\\ &= y * (1 - y) \end{align*} \]

2、tanh求导函数

\(y = \frac{e^x - e^{-x}}{e^x + e^{-x}}\)
求导过程：

\[ \begin{align*} \frac{dy}{dx} &= (\frac{e^x - e^{-x}}{e^x + e^{-x}})'\\ &= \frac{(e^x - e^{-x})'(e^x + e^{-x}) - (e^x - e^{-x})(e^x + e^{-x})'}{(e^x + e^{-x})^2}\\ &= \frac{(e^x + e^{-x})(e^x + e^{-x})-(e^x - e^{-x})(e^x - e^{-x})}{(e^x + e^{-x})^2}\\ &= 1 - \frac{(e^x - e^{-x})^2}{(e^x + e^{-x})^2}\\ &= 1 - (\frac{e^x - e^{-x}}{e^x + e^{-x}})^2\\ &= 1 - y ^ 2 \end{align*} \]

3、Relu求导函数

\(y = max(0, x)\)
可以简单推理出：当x < 0 时，\(\frac{dy}{dx} = 0\)；当 x >= 0 时，\(\frac{dy}{dx} = 1\)

参考原文：https://www.cnblogs.com/hutao722/p/9732223.html