【栈与队列】力扣232：用栈实现队列()

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：
实现 MyQueue 类：
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false
说明：
只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。
示例：

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]
解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

队列是一种 先进先出（first in - first out， FIFO）的数据结构，队列中的元素都从后端（rear）入队（push），从前端（front）出队（pop）。
栈是一种 后进先出（last in - first out， LIFO）的数据结构，栈中元素从栈顶（top）压入（push)，也从栈顶弹出（pop）。
实现队列最直观的方法是用链表。要用栈得到先入先出的结果，就必定要通过一个额外栈翻转一次数组。这个翻转过程既可以在插入时完成，也可以在取值时完成。可参考用栈实现队列 - 用栈实现队列 - 力扣（LeetCode）

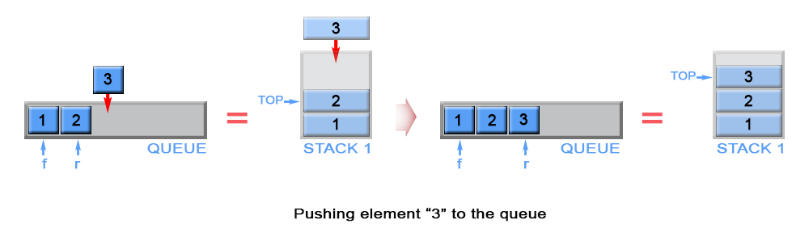
1. 插入值后完成翻转
   

• 入队：新元素总是压入 s1 的栈顶，同时把 s1 中压入的第一个元素赋值给作为队首元素的 front 变量。
  时间复杂度：O(1)。向栈压入元素的时间复杂度为O(1)
  空间复杂度：O(n)。需要额外的内存来存储队列元素
• 出队：为了弹出 s1 的栈底元素，需要把 s1 中所有的元素全部弹出，再把它们压入到另一个栈 s2 中，这个操作会让元素的入栈顺序反转过来。通过这样的方式，s1 中栈底元素就变成了 s2 的栈顶元素，这样就可以直接从 s2 将它弹出了。一旦 s2 变空了，只需把 s1 中的元素再一次转移到 s2 就可以了。
  时间复杂度：摊还复杂度 O(1)，最坏情况下的时间复杂度 O(n)。在最坏情况下，s2 为空，算法需要从 s1 中弹出 n 个元素，然后再把这 n 个元素压入 s2，在这里 n 代表队列的大小。这个过程产生了 2n 步操作，时间复杂度为 O(n)。但当 s2 非空时，算法就只有 O(1) 的时间复杂度。摊还分析给出了所有操作的平均性能，核心在于，最坏情况下的操作一旦发生了一次，那么在未来很长一段时间都不会再次发生，这样就会均摊每次操作的代价。
  空间复杂度 ：O(1)
• 取队首元素：定义了 front 变量来保存队首元素，每次 入队 操作都会随之更新这个变量。当 s2 为空，front 变量就是队首元素，当 s2 非空，s2 的栈顶元素就是队首元素。
  时间复杂度：O(1)。队首元素要么是之前就被计算出来的，要么就是 s2 栈顶元素
  空间复杂度：O(1)
• 判断空：s1 和 s2 都存有队列的元素，所以只需要检查 s1 和 s2 是否都为空就可以
  时间复杂度：O(1)
  空间复杂度：O(1)

class MyQueue:

    def __init__(self): # Initialize your data structure here.
        self.s1 = []
        self.s2 = []
        self.front = None # 保存队首元素，初始化为None，为peek操作作准备

    def push(self, x: int) -> None: # Push element x to the back of queue.
        if not self.s1: # s1为空时压入的元素就是第一个元素，即栈底（队首）元素
            self.front = x
        self.s1.append(x)

    def pop(self) -> int: # Removes the element from in front of queue and returns that element.
        if not self.s2: # s2为空时，往s2压入s1弹出的元素，直到s1为空
            while self.s1:
                self.s2.append(self.s1.pop())
        return self.s2.pop() # 此时从s2中弹出的元素顺序为s1自底向上的元素

    def peek(self) -> int: # Get the front element.
        # s1的队首元素本来应该是s1的栈底元素，转移给s2之后，如果队首元素为s2的栈顶元素
        if self.s2:
            return self.s2[-1]
        return self.front

    def empty(self) -> bool: # Return whether the queue is empty.
        # s1 和 s2 都存有队列的元素，所以只需要检查 s1 和 s2 是否都为空
        # return not (self.s1 or self.s2)
        # return not self.s1 and not s2
        if not self.s1 and not self.s2:
            return True
        return False

# Your MyQueue object will be instantiated and called as such:
# obj = MyQueue()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.peek()
# param_4 = obj.empty()

不是很懂，为什么peek操作不能用if not self.s1:，如果是在队列中间插入元素，此时s1、s2中都有元素，那这个时候peek应该是s1[0]才对吧？但是代码里又没有从s2把元素返回s1的相关操作，所以这个应该不在考虑范围？
没有变量front版本

class MyQueue(object):

    def __init__(self):
        self.stack1 = []
        self.stack2 = []

    def push(self, x):
        self.stack1.append(x)

    def pop(self):
        if not self.stack2:
            while self.stack1:
                self.stack2.append(self.stack1.pop())
        return self.stack2.pop()

    def peek(self):
        if not self.stack2:
            while self.stack1:
                self.stack2.append(self.stack1.pop())
        return self.stack2[-1]

    def empty(self):
        return not self.stack1 and not self.stack2

作者：fuxuemingzhu
链接：https://leetcode.cn/problems/implement-queue-using-stacks/solution/dong-hua-jiang-jie-ru-he-shi-yong-liang-6g7ub/

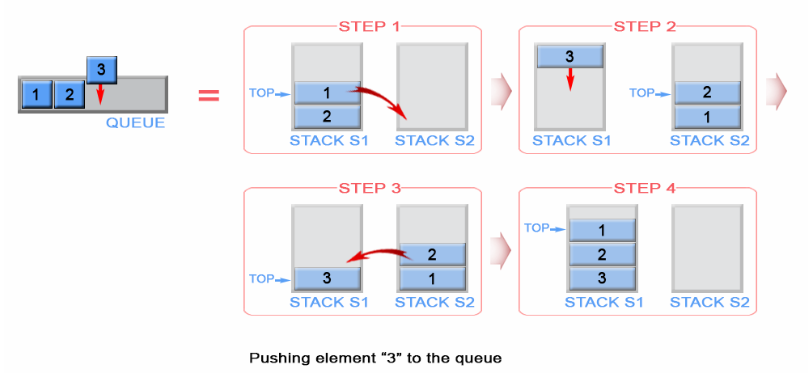
2. 插入值之前翻转
   
   这种情况下，反转操作后的元素都在s1中，与s2无关。

• 入队：一个队列是 FIFO 的，但一个栈是 LIFO 的。这就意味着最新压入的元素必须得放在栈底。为了实现这个目的，首先需要把 s1 中所有的元素移到 s2 中，接着把新元素压入 s2。最后把 s2 中所有的元素弹出，再把弹出的元素压入 s1。
  时间复杂度：O(n)。对于除了新元素之外的所有元素，它们都会被压入两次，弹出两次。新元素只被压入一次，弹出一次。这个过程产生了 4n + 2、 次操作，其中 n 是队列的大小。由于 压入 操作和 弹出 操作的时间复杂度为 O(1)，所以时间复杂度为 O(n)
  空间复杂度：O(n)。需要额外的内存来存储队列中的元素
• 出队：直接从 s1 弹出就可以了，因为 s1 的栈顶元素就是队列的队首元素。同时把弹出之后 s1 的栈顶元素赋值给代表队首元素的 front 变量。
  时间复杂度：O(1)
  空间复杂度：O(1)
• 取队首元素：用了 front 变量来存储队首元素，在每次 入队 操作或者 出队 操作之后这个变量都会随之更新。
  时间复杂度：O(1)。队首元素（front）已经被提前计算出来了，同时也只有 peek 操作可以得到它的值。
  空间复杂度：O(1)
• 判断空：s1 存储了队列所有的元素，所以只需要检查 s1 的是否为空就可以
  时间复杂度：O(1)
  空间复杂度：O(1)