【位运算】力扣190：颠倒二进制位

颠倒给定的 32 位无符号整数的二进制位。
提示：
请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在 示例 2 中，输入表示有符号整数 -3，输出表示有符号整数 -1073741825。
示例：

输入：n = 00000010100101000001111010011100
输出：964176192 (00111001011110000010100101000000)
解释：输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596，因此返回 964176192，其二进制表示形式为 00111001011110000010100101000000。

方法1：
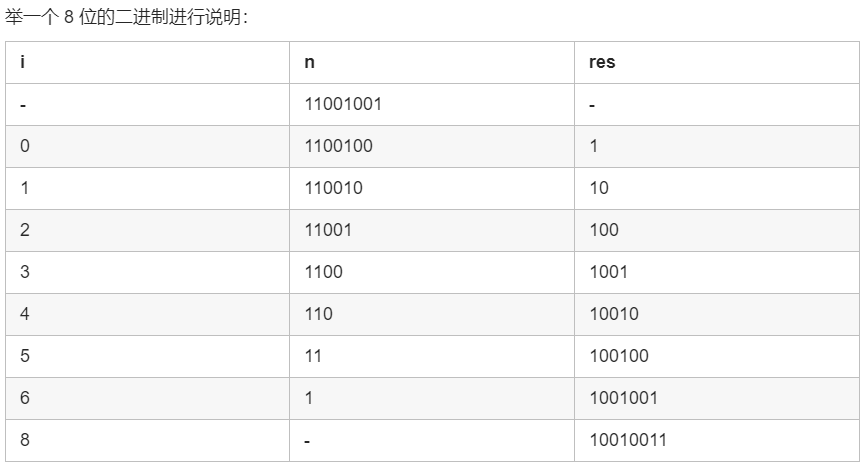
使用算术左移和右移，可以很轻易地实现二进制的翻转：每次把 res 左移，把 n 的二进制末尾数字，拼接到结果 res 的末尾。然后把 n 右移。

class Solution:
    def reverseBits(self, n: int) -> int:
        res = 0
        for i in range(32):
            # res = (res << 1) | (n & 1)
            res = res << 1
            res += n & 1 
            n >>= 1
        return res

时间复杂度：O(1)。
空间复杂度：O(1)。

方法2：分治法
有另外一种不使用循环的做法，类似于归并排序。
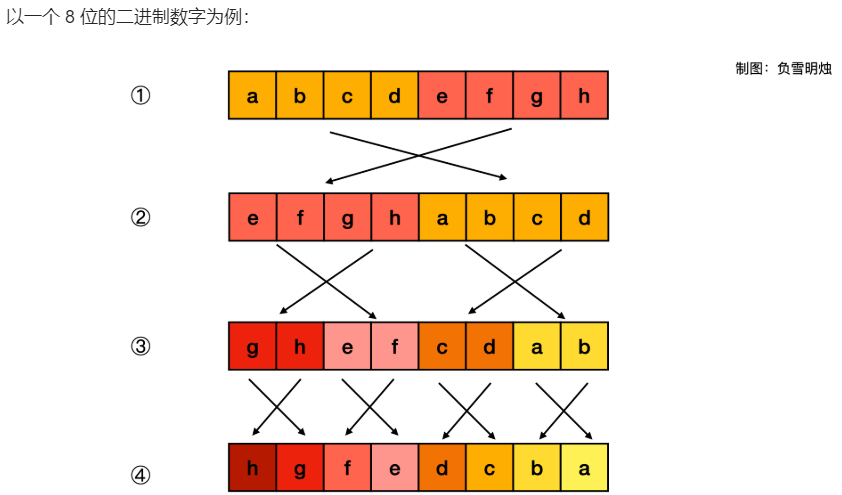
其思想是分而治之，把数字分为两半，然后交换这两半的顺序；然后把前后两个半段都再分成两半，交换内部顺序……直至最后交换顺序的时候，交换的数字只有 1 位。
也就是：
32位无符号整数，如 1111 1111 1111 1111 1111 1111 1111 1111
表示成16进制 f f f f f f f f
一个16进制的f代表二进制的4位
ffff ffff右移16位，变成 0000 ffff
ffff ffff左移16位，变成 ffff 0000
它们俩【相或】，就可以完成低16位与高16位的交换；
之后的每次分治，都要先【与】上一个掩码，再进行交换。

class Solution:
    # @param n, an integer
    # @return an integer
    def reverseBits(self, n):
        n = (n >> 16) | (n << 16) # 低16位与高16位交换
        n = ((n & 0xff00ff00) >> 8) | ((n & 0x00ff00ff) << 8) # 每16位中低8位和高8位交换；1111是f
        n = ((n & 0xf0f0f0f0) >> 4) | ((n & 0x0f0f0f0f) << 4) # 每8位中低4位和高4位交换
        n = ((n & 0xcccccccc) >> 2) | ((n & 0x33333333) << 2) # 每4位中低2位和高2位交换；1100是c，0011是3
        n = ((n & 0xaaaaaaaa) >> 1) | ((n & 0x55555555) << 1) # 每2位中低1位和高1位交换；1010是a，0101是5
        return n

作者：fuxuemingzhu
链接：https://leetcode.cn/problems/reverse-bits/solution/fu-xue-ming-zhu-xun-huan-yu-fen-zhi-jie-hoakf/

时间复杂度：O(1)
空间复杂度：O(1)