【数学】力扣528：按权重随机选择（review）

------------恢复内容开始------------

给你一个 下标从 0 开始 的正整数数组 w ，其中 w[i] 代表第 i 个下标的权重。 请你实现一个函数 pickIndex ，它可以 随机地 从范围 [0, w.length - 1] 内（含 0 和 w.length - 1）选出并返回一个下标。选取下标 i 的 概率 为 w[i] / sum(w) 。 例如，对于 w = [1, 3]，挑选下标 0 的概率为 1 / (1 + 3) = 0.25 （即，25%），而选取下标 1 的概率为 3 / (1 + 3) = 0.75（即，75%）。 示例： >输入： ["Solution","pickIndex","pickIndex","pickIndex","pickIndex","pickIndex"] [[[1,3]],[],[],[],[],[]] 输出： [null,1,1,1,1,0] 解释： Solution solution = new Solution([1, 3]); solution.pickIndex(); // 返回 1，返回下标 1，返回该下标概率为 3/4 。 solution.pickIndex(); // 返回 1 solution.pickIndex(); // 返回 1 solution.pickIndex(); // 返回 1 solution.pickIndex(); // 返回 0，返回下标 0，返回该下标概率为 1/4 。 由于这是一个随机问题，允许多个答案，因此下列输出都可以被认为是正确的: [null,1,1,1,1,0] [null,1,1,1,1,1] [null,1,1,1,0,0] [null,1,1,1,0,1] [null,1,0,1,0,0] ...... 诸若此类。

方法1：前缀和+二分查找
没有做过类似题目的话，一上来读题就觉得一头雾水。不知道题目想让我们返回什么。

• 首先一个测试用例输出的答案是不唯一的。
• 其次题目其实就是想让我们按照权重来 pickpick 一个数对应的 indexindex
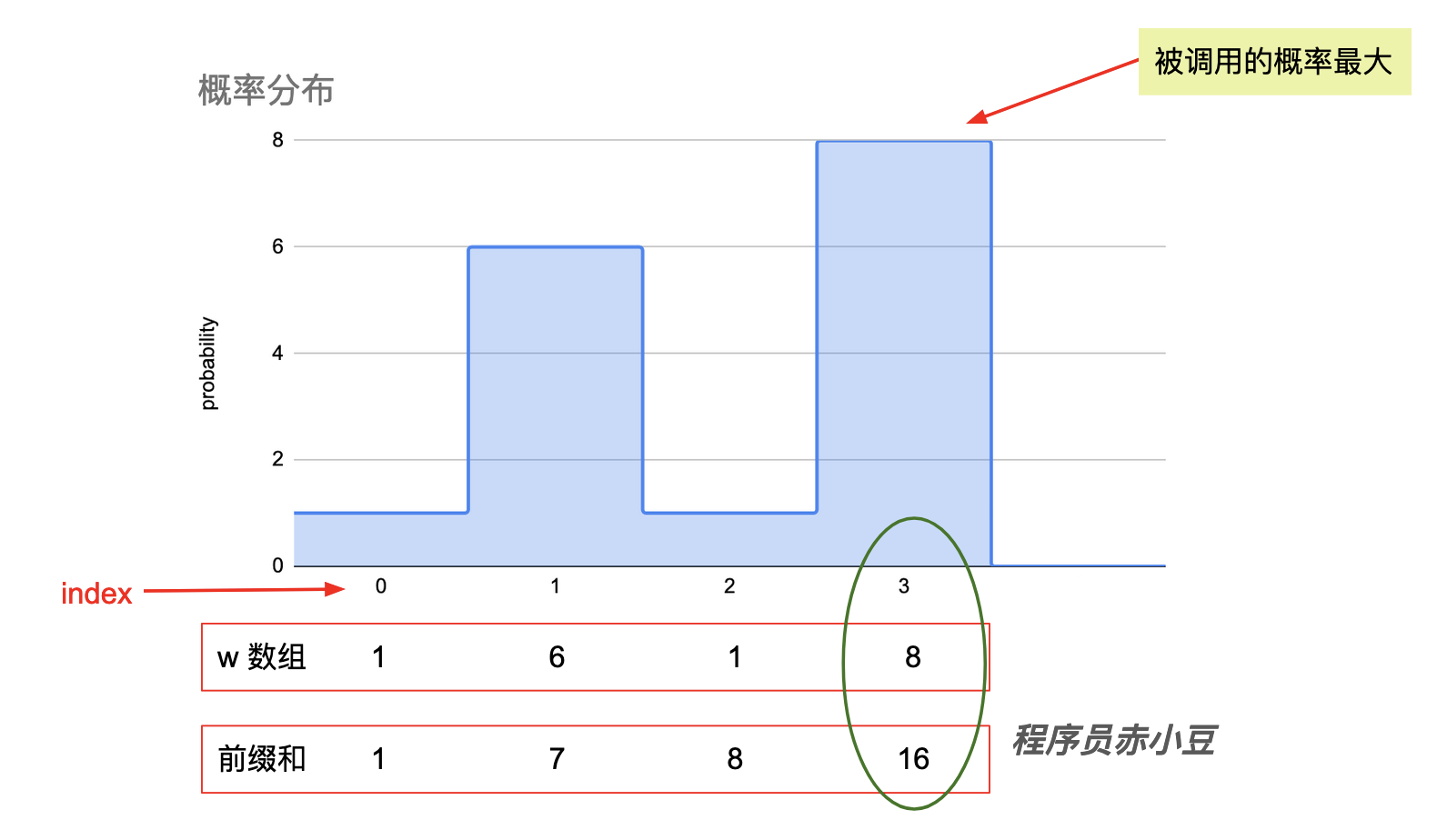
  • 比如数组 [1, 6, 1, 8]，每个元素代表一个权重，当一个函数请求过来的时候，我们应该从这个数组里面按照权重的优先级来进行分配
  • 上面数组对应的前缀和为 [1, 7, 8, 16]，我们可以发现，当一个数的权重越大的时候，它跟它前面的数可以拉开差距越大，比如 1 和 7 之间，比 7 和 8 之间的距离大。
  • 也就意味着当我们产生一个随机数，会有更大的概率落到 1~7 之间 或者 8~16 之间。
    
• 前缀和正好可以达成这个对应关系，数字越大的元素，它的权重越大，如果在这个前缀和里面掷骰子，概率分布式服从这个原则；
• 掷骰子的操作其实就是取一个随机数，随机数从前缀和数组中产生；
• 通过这个随机数，再定位到数组的下标即可。

算法思路：
设数组 w 的权重之和为 total。根据题目的要求，可以看成将 [1,total] 范围内的所有整数分成 n 个部分（其中 n 是数组 w 的长度），第 i 个部分恰好包含 w[i] 个整数，并且这 n 个部分两两的交集为空。随后我们在 [1,total] 范围内随机选择一个整数 x，如果整数 x 被包含在第 i 个部分内，我们就返回 i。
一种较为简单的划分方法是按照从小到大的顺序依次划分每个部分。例如 w=[3,1,2,4] 时，权重之和 total = 10，那么我们按照 [1, 3], [4, 4], [5, 6], [7, 10] 对 [1, 10] 进行划分，使得它们的长度恰好依次为 3, 1, 2, 4。可以发现，每个区间的左边界是在它之前出现的所有元素的和加上 1，右边界是到它为止的所有元素的和。因此，如果我们用 pre[i] 表示数组 w 的前缀和：$$ pre[i]= \sum_{k = 0}^iw[k] $$那么第 i 个区间的左边界就是 pre[i] − w[i] + 1，右边界就是 pre[i]。
当划分完成后，假设我们随机到了整数 x，我们希望找到满足
$ pre[i] − w[i] + 1 ≤ x ≤ pre[i] $ 的 i 并将其作为答案返回。
由于 pre[i] 是单调递增的，因此可以使用二分查找在 O(logn) 的时间内快速找到 i，即找出最小的满足 x ≤ pre[i] 的下标 i。

class Solution:

    def __init__(self, w: List[int]): # init是initially 的简写
        self.pre = list(accumulate(w))
        self.total = sum(w)

    def pickIndex(self) -> int:
        x = random.randint(1, self.total) # 生成随机数，包前包后
        return bisect_left(self.pre, x) # 二分查找：返回原序列中跟被插入元素相等的元素位置

# Your Solution object will be instantiated and called as such:
# obj = Solution(w)
# param_1 = obj.pickIndex()

时间复杂度：初始化的时间复杂度为 O(n)，每次选择的时间复杂度为 O(logn)，其中 n 是数组 w 的长度。
空间复杂度：O(n)，前缀和数组 pre 需要使用的空间。

方法2：轮盘赌
进化算法思想
和转盘抽奖一个意思，但这里的转盘理解成长条型，把所有数加起来就是转盘的长度 total。
随机从 1 到转盘长度中抽取一个数 x，然后挨个去减权重 w ，到 0 了就是这个家伙中奖了。

class Solution:

    def __init__(self, w: List[int]):
        self.w = w # 后面的函数没有定义数组w，所以要复制w传给后面
        self.total = sum(w) # 权重和，即转盘长度

    def pickIndex(self) -> int:
        x = random.randint(1, self.total) # 生成转盘长度内的随机数
        for i in range(0, len(self.w)):
            x -= self.w[i]
            if x <= 0:
                return i

# Your Solution object will be instantiated and called as such:
# obj = Solution(w)
# param_1 = obj.pickIndex()

作者：shi-zi-bo-tu-r
链接：https://leetcode.cn/problems/random-pick-with-weight/solution/python-7xing-shou-xi-de-lun-pan-du-by-sh-ztnk/

相比方法1耗时比较长，但是很好理解