【数学】力扣172：阶乘后的零

给定一个整数 n ，返回 n! 结果中尾随零的数量。
提示 n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1
示例：

输入：n = 3
输出：0
解释：3! = 6 ，不含尾随 0

一个数学结论题。

每个尾部的 0 由 2 × 5 = 10 而来，那么可以把阶乘的每一个元素拆成质数相乘，统计有多少个 2 和 5。显然，质因子 2 的数量远多于质因子 5 的数量，因此题目可以转化为阶乘里有多少个质因子 5。

class Solution:
    def trailingZeroes(self, n: int) -> int:
        # n 为 0 是一种特殊情况
        if n == 0:
            return 0
        count = 0
        for num in range(1, n + 1):
            while num % 5 == 0:
                num //= 5
                count += 1
        return count

时间复杂度：O(n)。
空间复杂度：O(1)。

第一个自己写的题！！！之前做过的行测题里有类似选择题所以知道思路。第一次没有通过是while写成了if，导致 25 这种含有多个 5 的数字只计入了一次。

参考官方解答，思路可以扩展一些，从num == 5开始计算，且每次增量5，因为n∈[0, 4]时count一定为0，而其他数不是5的倍数，没有必要考虑，如果n很大就可以节省很多时间。

class Solution:
    def trailingZeroes(self, n: int) -> int:
        count = 0
        for num in range(5, n + 1, 5):
            while num % 5 == 0:
                num /= 5
                count += 1
        return count

方法2：数学优化
一系列推导之后发现count其实就是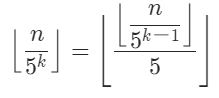
因此可以通过不断将 n 除以 5，并累加每次除后的 n，来得到答案。

class Solution:
    def trailingZeroes(self, n: int) -> int:
        ans = 0
        while n: # n > 0 时
            n //= 5
            ans += n
        return ans

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/factorial-trailing-zeroes/solution/jie-cheng-hou-de-ling-by-leetcode-soluti-1egk/

时间复杂度：O(logn)。
空间复杂度：O(1)。

一行代码：

class Solution:
    def trailingZeroes(self, n: int) -> int:
        return 0 if n == 0 else n // 5 + self.trailingZeroes(n // 5)

在C++中：

int trailingZeroes(int n) {
    return n == 0? 0: n / 5 + trailingZeroes(n / 5);
}