【双指针】力扣167：两数之和 II - 输入有序数组

给你一个下标从 1 开始的整数数组 numbers ，该数组已按非递减顺序排列  ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
示例：

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

看起来挺简单的，直接暴力破解超出时间限制

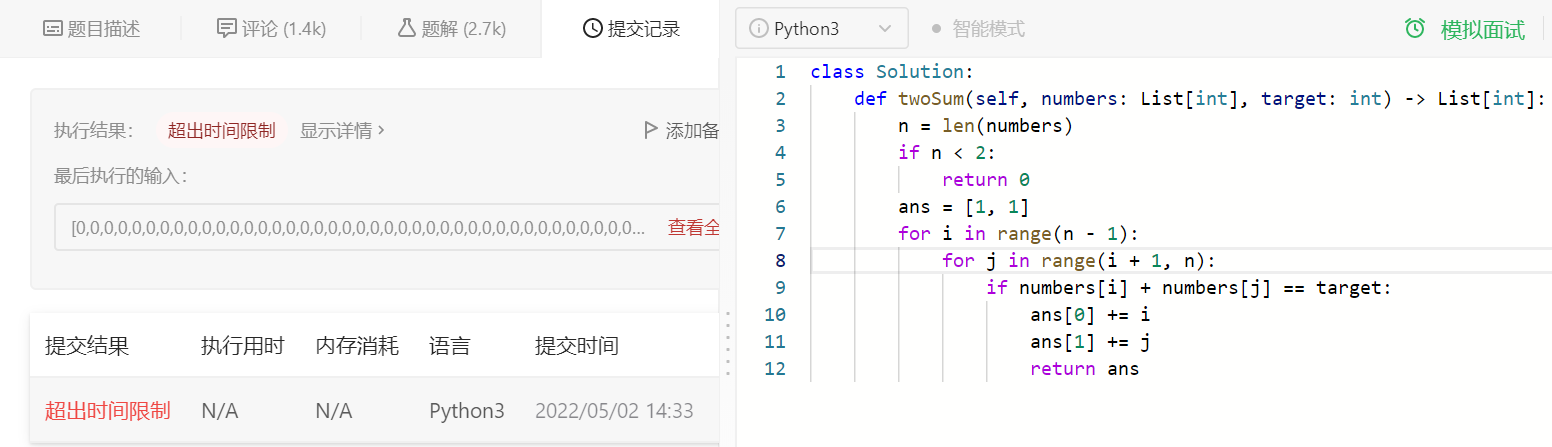
结合题目的【非递减顺序】数组，可以修改第二个指针从尾部开始遍历，根据相加结果判断哪个指针移动

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        i, j = 0, len(numbers) - 1
        while i < j:
            sum = numbers[i] + numbers[j]
            if sum == target:
                return [1 + i, 1 + j]
            elif sum < target:
                i += 1
            else:
                j -= 1
        return [-1, -1] # 未满足要求的情况，也可以 return[]

时间复杂度：O(n)，其中 n 是数组的长度。两个指针移动的总次数最多为 n 次。
空间复杂度：O(1)。

因为是有序数组，也可以用二分查找。
先固定一个数（一般是数组的第一个数），再利用low、high、mid找另一个数，判断是否满足要求

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        n = len(numbers)
        for i in range(n):
            low, high = i + 1, n - 1 # 为了保证i一定比mid小，low要比i大
            while low <= high:
                mid = (low + high) // 2
                sum = numbers[mid] + numbers[i]
                if sum == target:
                    return [i + 1, mid + 1] 
                elif sum < target:
                    low = mid + 1
                else:
                    high = mid - 1
        return []

时间复杂度：O(nlogn)，其中 n 是数组的长度。需要遍历数组一次确定第一个数，时间复杂度是 O(n)，寻找第二个数使用二分查找，时间复杂度是 O(logn)，因此总时间复杂度是 O(nlogn)。
空间复杂度：O(1)。