【搜索】力扣695:岛屿的最大面积
给定一个二维的 0-1 矩阵,其中 0 表示海洋, 1 表示陆地。单独的或相邻的陆地可以形成岛屿,每个格子只与其上下左右四个格子相邻。求最大的岛屿面积。
输入是一个二维数组,输出是一个整数,表示最大的岛屿面积。
示例:
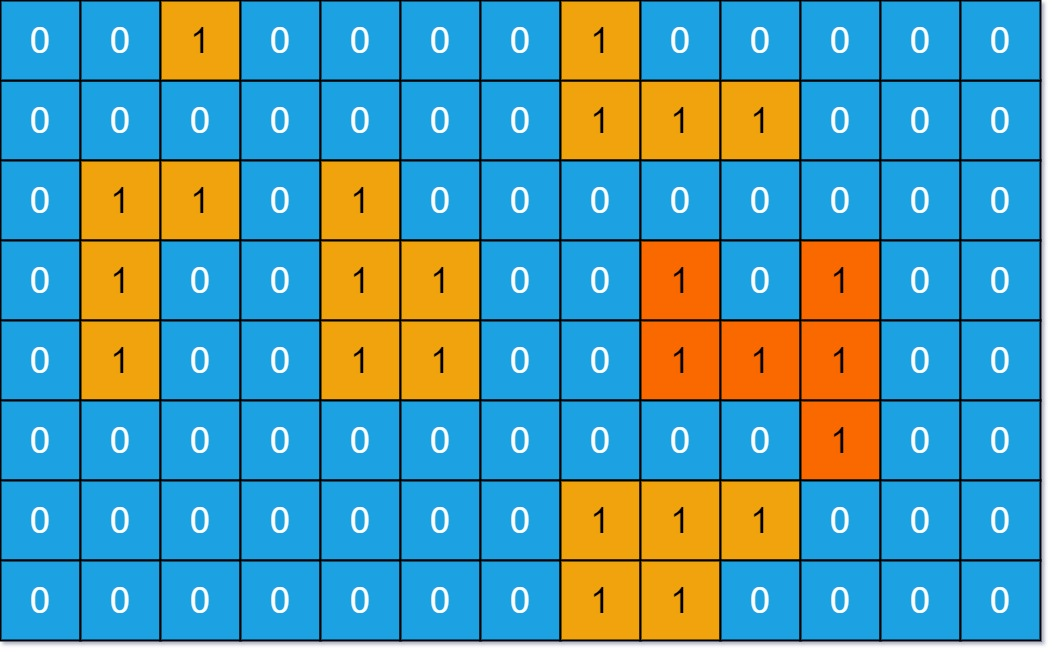
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出:6
解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
友情链接:一套模板,解决五个岛屿问题
1. 深度优先搜索(递归实现)
主函数用于遍历所有的搜索位置,判断是否可以开始搜索,如果可以就在辅函数进行搜索。
辅函数则负责深度优先搜索的递归调用。
-
目的:网格中每个连通形状的面积,然后取最大值
-
如果在一个土地上以 4 个方向探索与之相连的每一个土地(以及与这些土地相连的土地),那么探索过的土地总数将是该连通形状的面积
-
为了确保每个土地访问不超过一次,每次经过一块土地时,将这块土地的值置为 0。这样就不会多次访问同一土地
判定是否越界 与 进行下一步搜索 的先后关系都可以被接受
- 先判断:判断语句在辅函数中,在调用递归函数前
if not 0 <= x < m or not 0 <= y < n - 先搜索:判断语句在主函数的第一句
if grid[i][j] == 1:
以下代码两种判断都放了,可以删掉一个
class Solution:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
# 统计单个岛屿面积
def dfs(grid, x, y):
# 遇到左右边界或上下边界,或者该点为 0,就停止
if not 0 <= x < m or not 0 <= y < n or not grid[x][y]:
return
grid[x][y] = 0 # 已经统计了这个点,就标记为 0,保证不重复统计
self.area += 1 # 存储当前面积
# 上下左右继续遍历
dfs(grid, x, y - 1)
dfs(grid, x, y + 1)
dfs(grid, x - 1, y)
dfs(grid, x + 1, y)
return self.area # 全都找完了就输出这个岛的面积
res = 0 # 初始化最大面积为 0
m, n = len(grid), len(grid[0]) # 整个矩阵大小
# 找第一个陆地的开始
for i in range(m):
for j in range(n):
if grid[i][j] == 1: # 判定是否越界,只有在合法的情况下才进行下一步搜索
self.area = 0 # 每个岛单独统计,所以每次都要初始化当前岛面积为 0,再输入到 dfs 函数中
res = max(res, dfs(grid, i, j)) # 保留最大值,此时找过的岛已经全被标记为 0
return res
作者:yangyb25
链接:https://leetcode-cn.com/problems/max-area-of-island/solution/python-bfs-dfs-xiang-xi-zhu-shi-by-yangy-kh6i/
时间复杂度:O(R×C)。其中 R 是给定网格中的行数,C 是列数。我们访问每个网格最多一次。
空间复杂度:O(R×C),递归的深度最大可能是整个网格的大小,因此最大可能使用 O(R×C) 的栈空间。
2. 深度优先搜索(栈实现)
这种方法本质与方法 1 相同,使用栈(stack)实现深度优先搜索。区别是:
-
方法 1 通过函数的调用来表示接下来想要遍历哪些土地,让下一层函数来访问这些土地。而方法 2 把接下来想要遍历的土地放在 stack 里,然后在取出这些土地的时候访问它们
-
访问每一片土地时,对围绕它四个方向进行探索,找到还未访问的土地,加入到 stack 中
-
另外,只要 stack 不为空,就说明还有土地待访问,那么就从 stack 中取出一个元素并访问
因为栈与递归的调用原理相同,而递归相对便于实现,因此刷题时推荐使用递归式写法,同时也方便进行回溯。不过在实际工程上,直接使用栈可能才是最好的选择,一是因为便于理解,二是更不易出现递归栈满的情况。
class Solution:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
res = 0
m, n = len(grid), len(grid[0])
direction = [-1, 0, 1, 0, -1] # 相邻两两组合代表遍历方向 [0, 1], [0, -1], [1, 0], [-1, 0]
for i, a in enumerate(grid):
for j, num in enumerate(a):
cur = 0 # 当前面积
stack = [(i, j)] # 入栈
while stack:
cur_i, cur_j = stack.pop() # 当前位置
if cur_i < 0 or cur_j < 0 or cur_i == m or cur_j == n or grid[cur_i][cur_j] != 1:
continue # 不满足条件就跳出当前循环
cur += 1
grid[cur_i][cur_j] = 0 # 将统计过的点标记为 0
# 从这个点开始向四个方向遍历
'''
for k in range(4):
next_i, next_j = cur_i + direction[k], cur_j + direction[k + 1]
stack.append((next_i, next_j))
'''
for di, dj in [[0, 1], [0, -1], [1, 0], [-1, 0]]:
next_i, next_j = cur_i + di, cur_j + dj
stack.append((next_i, next_j))
res = max(res, cur)
return res
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/max-area-of-island/solution/dao-yu-de-zui-da-mian-ji-by-leetcode-solution/
时间复杂度:O(R×C)。其中 R 是给定网格中的行数,C 是列数。我们访问每个网格最多一次。
空间复杂度:O(R×C)。栈中最多会存放所有的土地,土地的数量最多为 R×C 块,因此使用的空间为O(R×C)。
3. 广度优先搜索
把方法 2 中的栈改为队列,每次从队首取出土地,并将接下来想要遍历的土地放在队尾,就实现了广度优先搜索算法。
class Solution:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
def bfs(grid, x, y):
queue = [[x, y]] # 第一个点加入队列
while queue: # 只要队列里面有东西就搜索
# 考虑当前最先进去的点
[x, y] = queue.pop(0)
if 0 <= x < len(grid) and 0 <= y < len(grid[0]) and grid[x][y]: # 不超界,或者不是 0,就继续搜索
grid[x][y] = 0 # 已经遍历过的点标记为 0
self.area += 1 # 记录当前面积
'''
bfs,下一次优先考虑每个点扩散开的矩阵
此处可能会加入不满足条件的点,但是因为在搜索前有条件判断,这些点在下一轮不会被考虑
'''
queue += [[x - 1, y], [x, y - 1], [x + 1, y], [x, y + 1]]
return self.area
res = 0
m, n = len(grid), len(grid[0])
# 找第一个陆地的开始
for i in range(m):
for j in range(n):
if grid[i][j] == 1:
self.area = 0 # 每个岛单独统计,初始化面积为 0
res = max(res, bfs(grid, i, j)) # 保留最大值,此时找过的点已经全被标记为 0
return res
作者:yangyb25
链接:https://leetcode-cn.com/problems/max-area-of-island/solution/python-bfs-dfs-xiang-xi-zhu-shi-by-yangy-kh6i/
时间复杂度:O(R×C)。其中 R 是给定网格中的行数,C 是列数。我们访问每个网格最多一次。
空间复杂度:O(R×C),队列中最多会存放所有的土地,土地的数量最多为 R×C 块,因此使用的空间为 O(R×C)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号