[LeetCode] 684. Redundant Connection _ Medium tag: Union Find

I

n this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

 

Example 1:

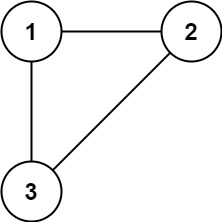
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

Example 2:

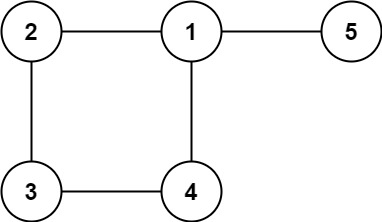
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

 

Constraints:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• There are no repeated edges.
• The given graph is connected.

 

Ideas:

参考[LeetCode] 261. Graph Valid Tree _ Medium tag: BFS这个里面union find的解法，如果找到union(a, b) is False，那么这就是重复的边，返回它即可。

Code

class UnionFind:
    def __init__(self, n):
        self.parent = [i for i in range(n)]
    
    def findRoot(self, a):
        while a != self.parent[a]:
            a = self.parent[a]
        return a
    
    def union(self, a, b):
        ra = self.findRoot(a)
        rb = self.findRoot(b)
        if ra == rb:
            return False
        self.parent[ra] = rb
        return True
    
class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        u = UnionFind(len(edges))
        for e1, e2 in edges:
            if not u.union(e1 - 1, e2 - 1):
                return [e1, e2]