软件工程第三次作业

最大连续子数和

一、问题描述及分析

• 问题描述

给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。

• 问题分析
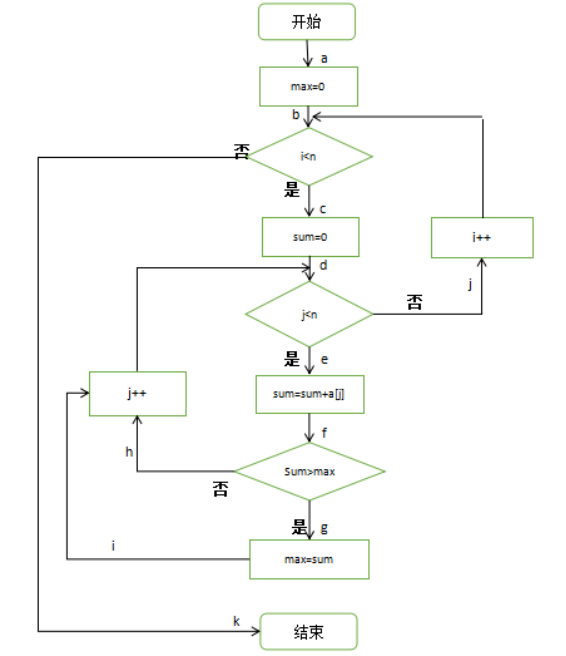
  该问题需要考虑两种情况：第一种是输入全为负时，则输出0；第二种是有正有负或全为正时输出最大连续子数和。
  我们可以定义一个Max代表最大的连续子数和，且Max初值为0；同时定义Sum，利用两层嵌套循环，从第i个数组元素开始遍历（i>=0）到最后一个元素并进行累加，将累加值赋予Sum（这里需注意：每进行一次外层循环，就需要给Sum赋初值0），每进行一次累加就将Sum值与Max值相比较，若Sum>Max,则将Sum值赋予Max，否则Max值不变；循环结束后 输出Max，即为所求值

二、相关代码分析

• 相关代码

#include<stdio.h>
#include<stdlib.h>
int Summax(int a[],int num)
{
	int max=0,sum,i,j;
   for(i=0;i<num;i++)
   {
	   sum=0;
	   for(j=i;j<num;j++)
	   {
	   sum=sum+a[j];
	   if(sum>max)
	   {
		   max=sum;
	   }
   }
	  
 }
    return max;
}
int main ()
{
	int a[50],n,i,max=0;
	scanf("%d",&n);
	for(i=0;i<n;i++)
	{ 
		scanf("%d",&a[i]);
	}
	max=Summax(a,n);
	printf("最大字段和为：%d\n",max);
	system("pause");
	return 0;
}

• 流程图
  
• coding地址
  https://dev.tencent.com/u/johnny_x/p/zuidalianxuzishuzuhe/git

三、运行结果及单元测试

• 运行结果
  
  
• 单元测试
  我选择的是判定条件覆盖
  第一组测试数据为：num=6，a[6]={-1,-2,-4,-6,-7,-2};路径为abcdefhjk
  第二组测试数据为：num=6，a[6]={-2,11,-4,13,-5,-2};路径为abcdefgijk
  测试代码如下：

[TestMethod]
		void TestMethod1()
		{
			int Max=0,i,j,sum;
			int num=6;
			array<int> ^a={-1,-2,-4,-6,-7,-2};
			 for(i=0;i<num;i++)
           {
	         sum=0;
	         for(j=i;j<num;j++)
	       {
	          sum=sum+a[j];
	         if(sum>Max)
	        {
		    Max=sum;
	        }
           }
	  
         }
			Assert::AreEqual(Max,0);
	   };
       [TestMethod]
		void TestMethod2()
		{
			int Max=0,i,j,sum;
			int num=6;
			array<int> ^a={-2,11,-4,13,-5,-2};
			 for(i=0;i<num;i++)
           {
	         sum=0;
	         for(j=i;j<num;j++)
	       {
	          sum=sum+a[j];
	         if(sum>Max)
	        {
		    Max=sum;
	        }
           }
	  
         }
			Assert::AreEqual(Max,20);
	   };

测试结果：