删边最短路

引入

给定一个无向连通图，保证 \(1\) 和 \(n\) 在同一个边双里，求删除每条边之后 \(1\) 到 \(n\) 的最短路。

解法

考虑先建出最短路树，显然删除非树边答案不变，现在只考虑删树边的情况。

推论：删除一条树边之后必然可以只经过一条非树边。

证明：

假设经过了两条非树边，若两条非树边不交，则不跨删除的树边的那条非树边是不优的。

若两条非树边相交：

蓝色的是树边，红色的是非树边，因为是最短路树，所以有 \(w(v_2,q)\leq w(v_2,v_3)+w(v_3,q)\)，与假设相悖。

同样可以证明 \(p\) 到 \(q\) 的路径上随便删一条都是正确的，问题在于如何寻找 \(p\) 和 \(q\)。

容易发现因为最终求的是 \(1\) 到 \(n\) 的最短路，所以 \(p\) 一定是 \(v_1\) 和 \(n\) 在最短路上的 LCA，同理，\(q\) 是 \(v_2\) 和 \(1\) 在反图最短路上的 LCA。

真的只要写两遍树剖就可以了？

然而会被这个卡掉：

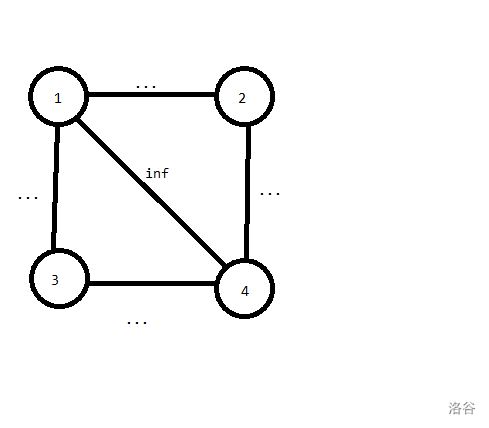
其中 \(w(1\rightarrow 2\rightarrow 4)=w(1\rightarrow 3\rightarrow 4)\)。

原因在于正图和反图的最短路可能不一样。

进一步发现只有 \(1\) 到 \(n\) 上的路径被删才可以产生新的解，所以只对 \(1\) 到 \(n\) 的边建线段树。继续考虑如何计算贡献：对不在路径上的每一个点计算其在路径上最左、最右的点 \(l_i\) 和 \(r_i\)。对于所有满足 \(l_u < r_v\) 非树边 \((u,v)\)，其可以更新的边是 \(l_u\) 到 \(r_v\) 的路径，证明是简单的。

然后就做完了，时间复杂度 \(O(n\log n)\)，瓶颈在于区间 \(min\) 单点查询。

代码

// P2685

#include<bits/stdc++.h>

using namespace std;

#define int long long
const int N=1e6+9;
const int inf=1e18;

struct node{
    int l,r,dat;
}tr[N<<2];
void Build(int x,int l,int r){
    tr[x].l=l;tr[x].r=r;tr[x].dat=inf;
    if(tr[x].l==tr[x].r) return ;
    int mid=tr[x].l+tr[x].r>>1;
    Build(x<<1,tr[x].l,mid);
    Build(x<<1|1,mid+1,tr[x].r);
}
void Modify(int x,int l,int r,int k){
    if(l<=tr[x].l&&tr[x].r<=r) return tr[x].dat=min(tr[x].dat,k),void();
    int mid=tr[x].l+tr[x].r>>1;
    if(l<=mid) Modify(x<<1,l,r,k);
    if(r>mid) Modify(x<<1|1,l,r,k);
}
pair<int,int> Merge(pair<int,int> p,pair<int,int> q){
    if(p.first==inf||q.first==inf) return min(p,q);
    else if(p.first==q.first) return {p.first,p.second+q.second};
    else return max(p,q);
}
pair<int,int> Query(int x,int cur){
    cur=min(cur,tr[x].dat);
    if(tr[x].l==tr[x].r) return {cur,1};
    else return Merge(Query(x<<1,cur),Query(x<<1|1,cur));
}

int fi[N],to[N<<1],ne[N<<1],w[N<<1],adj=1;
void AdEg(int x,int y,int z){
    ne[++adj]=fi[x];
    fi[x]=adj;
    to[adj]=y;
    w[adj]=z;
}
int dis[N],rdis[N],vis[N],n,m;
void Dij(int s,int *dis){
    for(int i=1;i<=n;i++) dis[i]=inf,vis[i]=0;
    priority_queue<pair<int,int>> q;
    dis[s]=0;
    q.push({0,s});
    while(q.size()){
        int x=q.top().second;
        q.pop();
        if(vis[x]) continue ;
        vis[x]=1;
        for(int i=fi[x];i;i=ne[i]){
            int y=to[i];
            if(vis[y]) continue ;
            if(dis[x]+w[i]>=dis[y]) continue ;
            dis[y]=dis[x]+w[i];
            q.push({-dis[y],y});
        }
    }
}
int pth[N],pv[N],pe[N],tot;
void FindPath(int s,int t){
    int pos=s;
    while(pos!=t){
        pv[pos]=1;
        pth[++tot]=pos;
        for(int i=fi[pos];i;i=ne[i]){
            int qos=to[i];
            if(rdis[pos]==rdis[qos]+w[i]){
                pos=qos;
                pe[i]=pe[i^1]=1;
                break ;
            }
        }
    }
    pv[pos]=1;
    pth[++tot]=pos;
}
int lv[N],rv[N];
void BFS(int c,int *dis,int *blg){
    queue<int> q;
    q.push(pth[c]);
    blg[pth[c]]=c;
    while(q.size()){
        int x=q.front();
        q.pop();
        for(int i=fi[x];i;i=ne[i]){
            int y=to[i];
            if(pv[y]) continue ;
            if(blg[y]) continue ;
            if(dis[x]+w[i]!=dis[y]) continue ;
            blg[y]=c;
            q.push(y);
        }
    }
}

signed main(){
    cin>>n>>m;
    for(int i=1,u,v,w;i<=m;i++){
        cin>>u>>v>>w;
        AdEg(u,v,w);
        AdEg(v,u,w);
    }

    Dij(1,dis);
    Dij(n,rdis);
    FindPath(1,n);
    for(int i=1;i<=n;i++) BFS(i,dis,lv);
    for(int i=n;i>=1;i--) BFS(i,rdis,rv);

    Build(1,1,tot);
    for(int x=1;x<=n;x++){
        for(int i=fi[x];i;i=ne[i]){
            int y=to[i];
            if(pe[i]) continue ;
            if(!lv[x]||!rv[y]) continue ;
            if(rv[y]<=lv[x]) continue ;
            Modify(1,lv[x],rv[y]-1,dis[x]+rdis[y]+w[i]);
        }
    }
    pair<int,int> ans=Query(1,inf);
    if(ans.first==inf) ans.first=dis[n];
    if(ans.first==dis[n]) ans.second=m;

    cout<<ans.first<<' '<<ans.second<<endl;

    return 0;
}