集训队互测 2025
Round 1
学生做了一整场 A,31+0+0 耻辱下播。
赛后发现 C 是签,自己做了不到 1h 就过了 /fn/fn/fn。
A. 携春同行
令 \(b_i\) 为 \(a\) 中第 \(i\) 大的数。
以每个点为根,构建菊花图,直径记为 \(d_i\),那么:
同时我们可以通过查询一条链求得 \(\displaystyle \sum_{i=1}^n b_i\),因此可以通过和式的加减求得 \(b_3\sim b_n\) 以及 \(b_1+b_2\)。
所以指向性已经十分明显了,我们需要求出 \(b_1\) 和 \(b_2\) 的位置,令其分别为 \(u\) 和 \(v\)。
将 \(d_u=b_1+b_2+b_3\) 染为黑色,否则染为白色,则 \(u\) 和 \(v\) 均为黑色。
考虑到 \(20\sim 2\log 500\lt \sqrt{500}\),这说明求解方法和二分关联很大。
考虑如下构造方式:
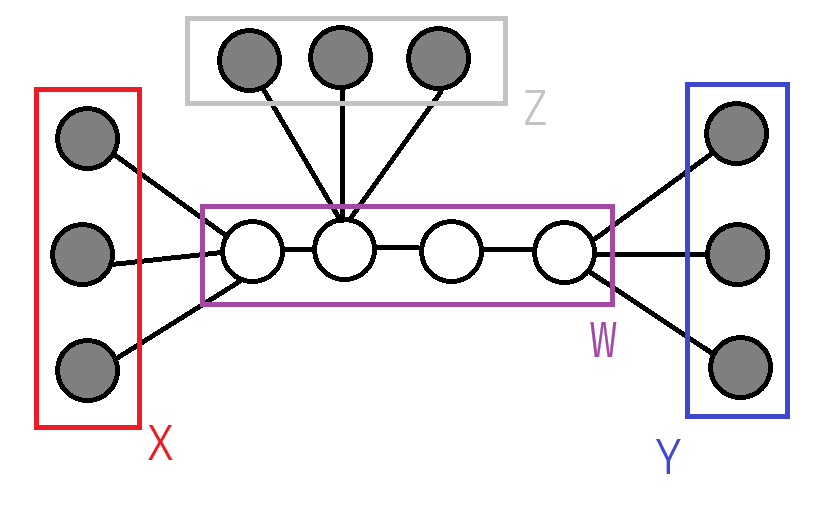
其中 \(W\) 为白色节点集合,\(X,Y,Z\) 是黑色节点构成的集合,\(X,Y\) 非空。如果 \(u,v\) 分居 \(X,Y\) 集合,那么直径长度恰好为 \(\displaystyle b_1+b_2+\sum_{u\in W} a_u\),否则小于这个值。因此我们可以用 1 次 guess 查询两个集合是否分别包含 \(u,v\)。
考虑如下流程:
- 二分黑色集合,令 \(X_i,Y_i\) 分别为二进制第 \(i\) 位为 \(0/1\) 的黑色节点构成的集合,找到第一组成功判断的 \(X_i,Y_i\) 并记录。
- 二分 \(X_i\),不失一般性地,令 \(u\in X_i\)。将 \(X_i\) 每次分拆为两个集合再利用 \(Y_i\) 判断哪个包含 \(u\),最终找到 \(u\)。
- 二分 \(Y_i\),先去除所有低 \(i\) 位和 \(u\) 不同的元素,然后执行和 \(X_i\) 一样的二分流程,找到 \(v\)。
这样的操作的 guess 次数是 \(i+(\log n-1)+(\log n-i-1) =2\log n-1\leq 17\) 的。
注意到上述判断要求白色节点至少有 3 个,因此在白色节点不够的时候还要转化部分黑色节点。
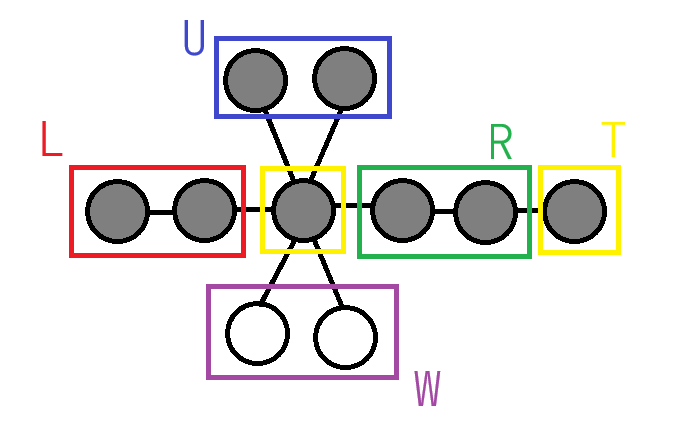
其中 \(W\) 是白色节点集合,黑色节点划分成三个均等的集合 \(L,R,U\),以及一个多余的集合 \(T\),要求 \(|T|>0\)。如果直径大小为 \(b_1+b_2+b_3(|L|+|R|+|T|-2)\),那么 \(u,v\notin U\),可以把 \(U\) 中的节点转成白色的。交换 \(L,R,U\) 重复这个过程,根据鸽巢原理,一定存在至少一个集合中没有 \(u\) 或 \(v\),且大小为 \(\lfloor\frac {n-1}3\rfloor \geq 3\)。同时这个过程只消耗 \(2\) 次 guess 操作,这是可以接受的。
至此,我们在至多 \(501\) 次 query 操作以及 \(19\) 次 guess 操作内完成了这题。
#include<bits/stdc++.h>
#include"haru.h"
using namespace std;
using ll=long long;
mt19937 rng(998244353);
vector<vector<int>> u,v;
inline void InsChain(int n){
u.push_back(vector<int>());
v.push_back(vector<int>());
for(int i=0;i<n-1;i++){
u.back().push_back(i);
v.back().push_back(i+1);
}
}
inline void InsFlower(int n,int root){
u.push_back(vector<int>());
v.push_back(vector<int>());
for(int i=0;i<n;i++){
if(i==root) continue ;
u.back().push_back(root);
v.back().push_back(i);
}
}
inline bool NotImp(vector<int> u,vector<int> l,vector<int> r,vector<int> trs,vector<int> d,ll val,ll t){
vector<int> e1,e2;
int c=trs.back(),lst=c;
trs.pop_back();
for(int i:u) e1.push_back(c),e2.push_back(i);
for(int i:d) e1.push_back(c),e2.push_back(i);
for(int i:l) e1.push_back(lst),e2.push_back(i),lst=i;
lst=c;
for(int i:r) e1.push_back(lst),e2.push_back(i),lst=i;
for(int i:trs) e1.push_back(lst),e2.push_back(i),lst=i;
ll q=t*(l.size()+r.size()+trs.size()-1)+val;
return guess(e1,e2,q);
}
inline bool Check(vector<int> x,vector<int> y,vector<int> z,vector<int> w,vector<int> ans,ll val){
vector<int> e1,e2;
int lst=w.front();
for(int i:w) if(i!=w.front()) e1.push_back(lst),e2.push_back(i),lst=i;
for(int i:x) e1.push_back(w.front()),e2.push_back(i);
for(int i:y) e1.push_back(w.back()),e2.push_back(i);
for(int i:z) e1.push_back(w[1]),e2.push_back(i);
ll q=val;
for(int i:w) q+=ans[i];
return guess(e1,e2,q);
}
vector<int> haru(int n){
u.clear(),v.clear();
for(int i=0;i<n;i++) InsFlower(n,i);
InsChain(n);
vector<ll> res=query(u,v);
vector<ll> tmp(res.begin(),prev(res.end()));
sort(tmp.begin(),tmp.end());
ll val=0;
for(int i=0;i<n;i++) val+=tmp[i];
val-=res.back();
val-=2*tmp.back();
val/=n-3;
ll t=tmp.back()-val;
vector<int> ans(n,-1),a,b;
for(int i=0;i<n;i++){
if(res[i]==tmp.back()){
a.push_back(i);
continue ;
}
ans[i]=res[i]-val;
b.push_back(i);
}
if(b.size()<=3){
vector<int> s[4];
int m=(a.size()-1)%3+1;
for(int i=0;i<a.size()-m;i++) s[i%3].push_back(a[i]);
for(int i=a.size()-m;i<a.size();i++) s[3].push_back(a[i]);
if(NotImp(s[0],s[1],s[2],s[3],b,val,t)){
for(int i:s[0]) ans[i]=t;
b.insert(b.end(),s[0].begin(),s[0].end());
s[0].clear();
}else if(NotImp(s[1],s[2],s[0],s[3],b,val,t)){
for(int i:s[1]) ans[i]=t;
b.insert(b.end(),s[1].begin(),s[1].end());
s[1].clear();
}else{
for(int i:s[2]) ans[i]=t;
b.insert(b.end(),s[2].begin(),s[2].end());
s[2].clear();
}
a.clear();
for(int i:{0,1,2,3}) a.insert(a.end(),s[i].begin(),s[i].end());
}
for(int w=0;w<60;w++){
vector<int> x,y;
for(int i:a){
if(~i>>w&1) x.push_back(i);
else y.push_back(i);
}
if(!x.size()||!y.size()) continue ;
if(Check(x,y,vector<int>(),b,ans,val)){
vector<int> trs;
while(x.size()>1){
vector<int> s[2];
for(int i=0;i<x.size();i++) s[i&1].push_back(x[i]);
vector<int> tmp=trs;
tmp.insert(tmp.end(),s[1].begin(),s[1].end());
if(Check(s[0],y,tmp,b,ans,val)){
x=s[0];
for(int i:s[1]) ans[i]=t;
trs.insert(trs.end(),s[1].begin(),s[1].end());
}else{
x=s[1];
for(int i:s[0]) ans[i]=t;
trs.insert(trs.end(),s[0].begin(),s[0].end());
}
}
int u=x.front();
vector<int> c;
for(int v:y){
if((u&(1<<w)-1)==(v&(1<<w)-1)) c.push_back(v);
else{
ans[v]=t;
trs.push_back(v);
}
}
while(c.size()>1){
vector<int> s[2];
for(int i=0;i<c.size();i++) s[i&1].push_back(c[i]);
vector<int> tmp=trs;
tmp.insert(tmp.end(),s[1].begin(),s[1].end());
if(Check(s[0],x,tmp,b,ans,val)){
c=s[0];
for(int i:s[1]) ans[i]=t;
trs.insert(trs.end(),s[1].begin(),s[1].end());
}else{
c=s[1];
for(int i:s[0]) ans[i]=t;
trs.insert(trs.end(),s[0].begin(),s[0].end());
}
}
int v=c.front();
break ;
}
}
return ans;
}
B. Everlasting Friends?
\(tp=1\)
让所有连通块的贡献在其深度最小的节点被计算,换言之,考虑对 \(T_{\max}\) 上的每一个子树分别计算贡献,并钦定根必须选。
我们希望找出一些可以被删除的点。首先所有在 \(T\) 上的边在 \(T_{\max}\) 上一定链接了一对祖先-后代,那么如果有一条 \(T_{\max}\) 上的边被至少两条 \(T\) 树边的点对覆盖,那么这条边向下连的儿子及其子树是不能删的,不然上面的点集一定不能在 \(T\) 中形成连通块。
至此已经刻画出连通块是否合法的关键性质,直接 DP 是 \(O(n^2)\) 的。但是发现每条边的性质最多变化一次,使用并查集维护,每次重构即可做到 \(O(n\log M)\)。
\(tp=2\)
首先,\(T_{\max}\) 和 \(T_{\min}\) 的共同连通块点集在 \(T\) 中依然是连通块,证明如下:
- 考虑抽出该点集在 \(T\) 上的极小斯坦纳树,由于该点集在 \(T_{\max}\) 上是连通块,因此斯坦纳树中只能包含该点集以及编号小于两边界点的点。
- 考虑抽出该点集在 \(T\) 上的极小斯坦纳树,由于该点集在 \(T_{\min}\) 上是连通块,因此斯坦纳树中只能包含该点集以及编号大于两边界点的点。
综上,点集在 \(T\) 上的极小斯坦纳树即为自身点集,同时显然是一个连通块。
令 \(x,y\) 分别为该点集的最大最小值,取出 \(x,y\) 在 \(T\) 上的路径,重复执行以下操作:
- 对于该点集领域中满足 \(x\geq z\geq y\) 的 \(z\),将 \(z\) 加入该点集。
可以证明的是,对于极大的这样的点集,这是唯一可能满足题设且最大最小值分别为 \(x,y\) 的点。原因是,令 \(w\) 为该点集中与 \(z\) 相连的点,在 \(T_{\max}\) 以 \(x\) 为根的子树和 \(T_{\min}\) 以 \(y\) 为根的子树之一中一定存在 \(w\) 为 \(z\) 祖先的情况。
进一步可以发现,该点集为 \(T_{\max}\) 以 \(x\) 为根的子树和 \(T_{\min}\) 以 \(y\) 为根的子树点集的交。因此考虑判断点对 \((x,y)\) 是否合法。
考虑点边容斥,对于每个点,它可以出现的范围是 \(T_{\max}\) 的一条链和 \(T_{\min}\) 上的一条链的交,而边则是两端点在两边的 LCA 的到根的链的交。那么如果点对 \((x,y)\) 是合法的,那么其子树内贡献之和为 \(2\),同时 \(y\) 在 \(x\) 子树内,\(x\) 在 \(y\) 子树内。
考虑使用线段树合并维护,在 \(T_{\max}\) 上跑,并维护在 \(T_{\min}\) 上的贡献,并查询点权最小值是否为 \(2\) 并统计最小值个数。注意还要满足 \(y\) 在 \(x\) 子树内,\(x\) 在 \(y\) 子树内。\(x\) 在 \(y\) 子树内可以通过仅查询 \(x\) 在 \(T_{\min}\) 上到根链上的 \(y\) 限制。\(y\) 在 \(x\) 子树内可以通过将 \(x\) 子树内所有点,即遍历过的点,的点权全部减去一,从而变成查询最小值是否为 \(1\) 来限制。时间复杂度 \(O(n\log^2 n)\)。
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
using ll=long long;
const int N=2e5+9;
const int lgN=2e1;
const int mod=998244353;
inline void AddAs(int &x,int y){if((x+=y)>=mod) x-=mod;}
inline void SubAs(int &x,int y){if((x-=y)<0) x+=mod;}
inline void MulAs(int &x,int y){x=1ll*x*y%mod;}
inline int Add(int x,int y){if((x+=y)>=mod) x-=mod;return x;}
inline int Sub(int x,int y){if((x-=y)<0) x+=mod;return x;}
inline int Mul(int x,int y){return 1ll*x*y%mod;}
inline int QPow(int x,int y){
int res=1;
while(y){
if(y&1) MulAs(res,x);
MulAs(x,x);
y>>=1;
}
return res;
}
inline int Inv(int x){return QPow(x,mod-2);}
int typ,n;
vector<int> e[N];
namespace Case1{
struct Zint{
int x,z;
Zint(){}
Zint(int _x){x=_x?_x:1,z=_x?0:1;}
Zint(int _x,int _z){*this=Zint(_x),z+=_z;}
inline Zint friend operator +(Zint a,Zint b){
if(a.z>b.z) return b;
else if(a.z<b.z) return a;
else return Zint(Add(a.x,b.x),a.z);
}
inline Zint friend operator -(Zint a){return Zint(Sub(0,a.x),a.z);}
inline Zint friend operator -(Zint a,Zint b){return a+(-b);}
inline Zint friend operator *(Zint a,Zint b){return Zint(Mul(a.x,b.x),a.z+b.z);}
inline Zint friend operator /(Zint a,Zint b){return Zint(Mul(a.x,Inv(b.x)),a.z-b.z);}
inline int Val(){return assert(z>=0),!z?x:0;}
};
int fa[N],to[N];
inline void Init(int lim){iota(fa+1,fa+lim+1,1);}
inline int Find(int x){return x==fa[x]?x:fa[x]=Find(fa[x]);}
inline void Merge(int x,int y){fa[Find(y)]=Find(x);}
Zint f[N];
inline void Solve(){
Init(n);
int ans=0;
for(int u=1;u<=n;u++){
f[u]=Zint(1);
for(int v:e[u]){
if(v>u) continue ;
Zint tmp(1);
for(int r=Find(v);to[r];r=Find(r)){
tmp=tmp*(f[r])/(f[r]+Zint(1));
Merge(to[r],r);
}
f[Find(v)]=f[Find(v)]*tmp;
f[u]=f[u]*(f[Find(v)]+Zint(1));
to[Find(v)]=u;
}
AddAs(ans,f[u].Val());
}
cout<<ans<<endl;
}
}
namespace Case2{
struct Node{
int lc,rc,tag;
array<int,2> dat;
}tr[N<<6];
#define lc(x) tr[x].lc
#define rc(x) tr[x].rc
#define tag(x) tr[x].tag
#define dat(x) tr[x].dat
int trs[N<<6],cnt,tot;
inline int Allc(int len){
int x=tot?trs[tot--]:++cnt;
tag(x)=0,dat(x)={0,len};
return x;
}
inline void DeAllc(int x){
trs[++tot]=x;
lc(x)=rc(x)=tag(x)=0;
dat(x)={0,0};
}
inline array<int,2> Calc(array<int,2> a,array<int,2> b){
if(a[0]^b[0]) return min(a,b);
else return {a[0],a[1]+b[1]};
}
inline void PushUp(int x,int L,int R){
int mid=L+R>>1;
dat(x)=Calc(lc(x)?dat(lc(x)):array<int,2>({0,mid-L+1}),rc(x)?dat(rc(x)):array<int,2>({0,R-mid}));
dat(x)[0]+=tag(x);
}
inline void Push(int x,int k){dat(x)[0]+=k,tag(x)+=k;}
inline void Modify(int &x,int L,int R,int l,int r,int k){
if(!x) x=Allc(R-L+1);
if(l<=L&&R<=r) return Push(x,k);
int mid=L+R>>1;
if(l<=mid) Modify(lc(x),L,mid,l,r,k);
if(r>mid) Modify(rc(x),mid+1,R,l,r,k);
PushUp(x,L,R);
}
inline array<int,2> Query(int x,int L,int R,int l,int r){
if(!x) return {0,min(R,r)-max(L,r)+1};
if(l<=L&&R<=r) return dat(x);
int mid=L+R>>1;
array<int,2> res;
if(r<=mid) res=Query(lc(x),L,mid,l,r);
else if(l>mid) res=Query(rc(x),mid+1,R,l,r);
else res=Calc(Query(lc(x),L,mid,l,r),Query(rc(x),mid+1,R,l,r));
res[0]+=tag(x);
return res;
}
inline void Merge(int &x,int &y,int L,int R){
if(!x||!y) return x=x|y,void();
tag(x)+=tag(y);
if(L==R){
PushUp(x,L,R);
DeAllc(y);
return ;
}
int mid=L+R>>1;
Merge(lc(x),lc(y),L,mid),Merge(rc(x),rc(y),mid+1,R);
PushUp(x,L,R);
DeAllc(y);
}
int f[N];
struct Tree{
vector<int> e[N];
inline vector<int>& operator [](int x){return e[x];}
int fa[N],elr[N<<1],pos[N<<1],root,ecnt;
inline void DFS(int x){
elr[++ecnt]=x;
pos[x]=ecnt;
for(int y:e[x]){
if(fa[x]==y) continue ;
fa[y]=x;
DFS(y);
elr[++ecnt]=x;
}
}
int mn[N<<1][lgN],lg[N<<1];
inline void Init(int r){
root=r,DFS(r);
for(int i=2;i<=ecnt;i++) lg[i]=lg[i>>1]+1;
for(int i=1;i<=ecnt;i++) mn[i][0]=pos[elr[i]];
for(int k=1;k<=lg[ecnt];k++){
for(int i=1;i<=ecnt-(1<<k)+1;i++){
mn[i][k]=min(mn[i][k-1],mn[i+(1<<k-1)][k-1]);
}
}
}
inline int LCA(int x,int y){
x=pos[x],y=pos[y];
if(x>y) swap(x,y);
int k=lg[y-x+1];
return elr[min(mn[x][k],mn[y-(1<<k)+1][k])];
}
}t0,t1;
inline void Init(int lim){iota(f+1,f+lim+1,1);}
inline int Find(int x){return x==f[x]?x:f[x]=Find(f[x]);}
inline void Merge(int x,int y){f[Find(y)]=Find(x);}
inline void GetT0(){
Init(n);
for(int i=1;i<=n;i++){
for(int j:e[i]){
if(j>i) continue ;
t0[i].push_back(Find(j));
Merge(i,Find(j));
}
}
t0.Init(n);
}
inline void GetT1(){
Init(n);
for(int i=n;i>=1;i--){
for(int j:e[i]){
if(j<i) continue ;
t1[i].push_back(Find(j));
Merge(i,Find(j));
}
}
t1.Init(1);
}
int fa[N],dep[N],siz[N],hson[N];
inline void GetHSon(int x){
siz[x]=1;
for(int y:t1[x]){
fa[y]=x;
dep[y]=dep[x]+1;
GetHSon(y);
siz[x]+=siz[y];
if(!hson[x]||siz[y]>siz[hson[x]]) hson[x]=y;
}
}
int dfn[N],top[N],dcnt;
inline void GetTop(int x,int t){
top[x]=t;
dfn[x]=++dcnt;
if(hson[x]) GetTop(hson[x],t);
for(int y:t1[x]){
if(y==hson[x]) continue ;
GetTop(y,y);
}
}
int root[N],ans;
vector<array<int,2>> mdf[N];
inline void AddToRoot(int &root,int x,int k){
while(x){
Modify(root,1,n,dfn[top[x]],dfn[x],k);
x=fa[top[x]];
}
}
inline array<int,2> QueryToRoot(int root,int x){
array<int,2> res={INT_MAX,0};
while(x){
res=Calc(res,Query(root,1,n,dfn[top[x]],dfn[x]));
x=fa[top[x]];
}
return res;
}
inline void Work(int x){
for(int y:t0[x]){
Work(y);
Merge(root[x],root[y],1,n);
}
Modify(root[x],1,n,dfn[x],dfn[x],-1);
for(auto t:mdf[x]) AddToRoot(root[x],t[0],t[1]);
array<int,2> res=QueryToRoot(root[x],x);
if(res[0]==1) AddAs(ans,res[1]);
}
inline void Solve(){
GetT0(),GetT1();
GetHSon(1),GetTop(1,1);
for(int i=1;i<=n;i++){
mdf[i].push_back({i,2});
for(int j:t0[i]) mdf[t0.LCA(i,j)].push_back({t1.LCA(i,j),-1});
for(int j:t1[i]) mdf[t0.LCA(i,j)].push_back({t1.LCA(i,j),-1});
}
Work(n);
cout<<ans<<endl;
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>typ>>n;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}
if(typ==1) Case1::Solve();
else Case2::Solve();
return 0;
}
C. 集你太美
考虑如何刻画 收集-free 的条件,下文中令 \(W_i\) 表示点权初始值,\(w_i\) 表示当前点权。
发现除去边权为 0 的边之后,如果这个图是 收集-free 的,那么必然存在按某种顺序重复操作某一个连通块的所有节点的方案,否则难以保持每个点的点权,毕竟总和不变。进一步探索,令 \(ord_i\) 表示 \(i\) 被操作的时刻,当我们在操作 \(i\) 节点之前,\(i\) 节点的权值应该是 \(\displaystyle W_i+\sum_{(i,j)\in E} -v_{i,j}[ord_j\lt ord_i]\),我们希望这个值非负。
\(o=1\)
我们知道 \(\displaystyle W_i+\sum_{(i,j)\in E} -v_{i,j}[ord_j\lt ord_i]\geq 0\),因此有 \(\displaystyle \sum_{i=1}^n W_i\geq \sum_{i=1}^n\sum_{(i,j)\in E} v_{i,j}[ord_j\lt ord_i]=\sum_{(i,j)\in E} v_{i,j}\)。这个下界显然是可以取到的,令 \(\displaystyle W_i=\sum_{(i,j)\in E} v_{i,j}[j\lt i],ord_i=i\) 即可。
\(o=2\)
直接做看起来不是很好做,想到 Bamboo。
正难则反,考虑将操作转为令 \(\forall (i,j)\in E,w_j\leftarrow w_j+v_{i,j}\) 并且令 \(\displaystyle w_i\leftarrow w_i-\sum_{(i,j)\in E} v_{i,j}\),要求此时 \(\displaystyle w_i\geq\sum_{(i,j)\in E} v_{i,j}\),收集-free 的条件转为可以通过这种方式把连通块内所有点操作一遍。经转化后,显然操作未操作过的满足 \(\displaystyle w_i\geq\sum_{(i,j)\in E} v_{i,j}\) 的 \(i\) 不会影响合法性,毕竟转化后的操作只会让 \(w_j\) 变大。对每个连通块判断一遍即可。
时间复杂度 \(O(n\alpha(n))\)。
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=3e5+9;
int n,m,o;
vector<array<int,2>> e[N];
ll a[N],d[N];
ll siz[N];
int fa[N];
inline void Init(int lim){for(int i=1;i<=lim;i++) fa[i]=i;}
inline int Find(int x){return fa[x]==x?x:fa[x]=Find(fa[x]);}
inline void Merge(int x,int y){
x=Find(x),y=Find(y);
if(x==y) return ;
fa[y]=x;
}
int vis[N];
vector<int> p[N];
inline bool Check(vector<int> node){
int cnt=0;
queue<int> q;
for(int x:node) if(a[x]>=d[x]) vis[x]=1,q.push(x);
while(q.size()){
int x=q.front();
q.pop();
cnt++;
for(auto t:e[x]){
int y=t[0];
a[x]-=t[1],a[y]+=t[1];
if(!vis[y]&&a[y]>=d[y]) vis[y]=1,q.push(y);
}
}
return cnt==node.size();
}
signed main(){
cin>>o>>n>>m;
Init(n);
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
if(!w) continue ;
e[u].push_back({v,w});
e[v].push_back({u,w});
d[u]+=w,d[v]+=w;
Merge(u,v);
siz[Find(u)]+=w;
}
if(o==1){
int x=0;
for(int i=1;i<=n;i++){
if(i!=fa[i]) continue ;
if(!x||siz[i]<siz[x]) x=i;
}
for(int i=1;i<=n;i++){
if(Find(i)!=x) continue ;
for(auto t:e[i]){
if(Find(t[0])!=x) continue ;
if(i<t[0]) a[i]+=t[1];
}
}
for(int i=1;i<=n;i++) cout<<a[i]<<' ';cout<<endl;
}else{
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) p[Find(i)].push_back(i);
for(int i=1;i<=n;i++){
if(i!=fa[i]) continue ;
if(Check(p[i])){
cout<<"YES"<<endl;
return 0;
}
}
cout<<"NO"<<endl;
}
return 0;
}
Round 3
A. 火花
由于 \(t\) 的限制和子树强相关,而 \(k\) 的限制是树上依赖背包,因此考虑在欧拉序上做文章。
令 \(e_i\) 为欧拉序上第 \(i\) 个节点,\(l_u\) 表示 \(u\) 在欧拉序上第一次出现的位置,\(r_u\) 示 \(u\) 在欧拉序上第二次出现的位置。
设 \(f_{i,j,p}\) 表示当前考虑到欧拉序第 \(i\) 位,剩 \(j\) 个选点额度,\(p\) 个到根路径额度,初始有 \(f_{1,k,t}=1\)。
-
若 \(i=l_{e_{i}}\):
- 若当前子树不选:有转移 \(f_{r_{e_i}+1,j,p-q}\leftarrow f_{i,j,p}+w_{e_i}(q)\),其中 \(w_x(q)\) 表示 \(x\) 到根路径和中前 \(q\) 大的和,\(q\in[0,p]\)。
- 若当前子树选:发现在 \(l_x\) 和 \(r_x\) 处单独转移都不是很好做,因为没有办法直接获取到子树内到选了几个到根路径,从而无法直接得到 \(e_i\) 单独选取的实际上界。因此直接「王の钦定」,将 \(c_x-p\) 个在 \(l_x\) 处转移,而 \(p-q\) 个在 \(r_x\) 处转移,其中 \(q\) 是 \(x\) 子树内到根路径的个数。因此在此处有转移 \(f_{i+1,j-q,p}\leftarrow f_{i,j,p}+q\cdot a_{e_i}\),\(q\in[1,\min(c_x-p,j)]\)。
-
若 \(i=r_{e_i}\):
此时的 \(p\) 就是 \(e_i\) 剩余的额度。
- 若 \(x\) 未消耗到根的额度:有转移 \(f_{i+1,j-q,p}\leftarrow f_{i,j,p}+q\cdot a_{e_i}\),\(q\in[0,\min(j,p)]\)。
- 若 \(x\) 未消耗到根的额度:有转移 \(f_{i+1,j-q,p-1}\leftarrow f_{i,j,p}+q\cdot a_{e_i}+s_{e_i}\),其中 \(s_x\) 表示 \(x\) 到根路径和,\(q\in[0,\min(j,p-1)]\)。
除了 \(i=l_{e_{i}}\) 当前子树不选的情况,剩下的对于 \(j\) 这一维都是多重背包转移,可以单调队列优化。
而 \(i=l_{e_{i}}\) 当前子树不选的情况下,是一个 1D1D 代价为 \(w_x(p-p')\) 的 DP,而 \(w_x(i)\) 显然是一个上凸函数,换言之,满足四边形不等式,可以直接决策单调性分治转移,时间复杂度 \(O(nkt\log t)\)。
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
using ll=long long;
const int N=1e4+9;
const ll inf=1e18;
template<class T> inline void ChMax(T &x,T y){if(y>x) x=y;}
vector<int> e[N];
ll s[N],su[N][N];
int c[N],v[N],fa[N],siz[N],l[N],r[N],elr[N<<1],n,k,t,ecnt;
inline void DFS(int x){
elr[l[x]=++ecnt]=x;
su[x][siz[x]=1]=s[x]=s[fa[x]]+v[x];
for(int y:e[x]){
fa[y]=x;
DFS(y);
vector<ll> tmp(siz[x]+siz[y]);
merge(su[x]+1,su[x]+siz[x]+1,su[y]+1,su[y]+siz[y]+1,tmp.begin(),greater<ll>());
copy(tmp.begin(),tmp.end(),su[x]+1);
siz[x]+=siz[y];
}
elr[r[x]=++ecnt]=x;
}
inline void Conquer(int x,vector<ll> &f,vector<ll> &g,int l,int r,int vl,int vr){
if(l>r) return ;
int mid=l+r>>1;
array<ll,2> tmp={-inf,0};
for(int i=mid;i<=vr;i++) ChMax(tmp,{f[i]+su[x][i-mid],i});
int mp=tmp[1];
ChMax(g[mid],f[mp]+su[x][mp-mid]);
if(tmp[0]>=0) Conquer(x,f,g,l,mid-1,vl,mp);
Conquer(x,f,g,mid+1,r,mp,vr);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>k>>t;
for(int i=1;i<=n;i++) cin>>c[i]>>v[i];
for(int i=2,f;i<=n;i++) cin>>f,e[f].push_back(i);
DFS(1);
for(int x=1;x<=n;x++){
for(int i=1;i<=siz[x];i++) su[x][i]+=su[x][i-1];
}
vector<vector<vector<ll>>> f(ecnt+2,vector<vector<ll>>(k+1,vector<ll>(t+1,-inf)));
f[1][k][t]=0;
for(int i=1;i<=ecnt;i++){
int x=elr[i];
if(i==l[x]){
for(int p=0;p<=t;p++){
list<int> li;
auto W=[&](int j,int _j){return f[i][_j][p]+1ll*(_j-j)*v[x];};
for(int j=k-1;~j;j--){
while(li.size()&&j+c[x]-p<li.front()) li.pop_front();
while(li.size()&&W(j,li.back())<W(j,j+1)) li.pop_back();
li.push_back(j+1);
if(li.size()) ChMax(f[i+1][j][p],W(j,li.front()));
}
}
for(int j=0;j<=k;j++) Conquer(x,f[i][j],f[r[x]+1][j],0,t,0,t);
}else{
for(int p=0;p<=t;p++){
list<int> li;
auto W=[&](int j,int _j){return f[i][_j][p]+1ll*(_j-j)*v[x];};
for(int j=k;~j;j--){
while(li.size()&&j+p<li.front()) li.pop_front();
while(li.size()&&W(j,li.back())<W(j,j)) li.pop_back();
li.push_back(j);
if(li.size()) ChMax(f[i+1][j][p],W(j,li.front()));
}
}
for(int p=0;p<t;p++){
list<int> li;
auto W=[&](int j,int _j){return f[i][_j][p+1]+1ll*(_j-j)*v[x]+s[x];};
for(int j=k;~j;j--){
while(li.size()&&j+p<li.front()) li.pop_front();
while(li.size()&&W(j,li.back())<W(j,j)) li.pop_back();
li.push_back(j);
if(li.size()) ChMax(f[i+1][j][p],W(j,li.front()));
}
}
}
}
ll ans=0;
for(int j=0;j<=k;j++){
for(int p=0;p<=t;p++) ChMax(ans,f[ecnt+1][j][p]);
}
cout<<ans<<endl;
return 0;
}
C. 少年汹涌
不妨先考虑 \(n=1\) 怎么做。
注意到 \(w_i\leq 62\lt 64=2^6\),因此每次操作之后 \(\lfloor x/64\rfloor\) 的变化量至多是 \(1\)。因此每次操作其实可以重复操作直到 \(\lfloor x/64\rfloor\) 变化,即将 $\lfloor x/64\rfloor $ 相同的操作绑在一起,每次强制向高位进一且只进一,这样高位的变化就是一个遍历了。
进一步地,考虑对上面的东西倍增,令 \(f_{i,s,k}\) 和 \(g_{i,s,k}\) 分别表示 \(\operatorname{popcount}(\lfloor x/64\rfloor)=i,s=x\bmod 64\) 时,遍历一个 \(2^k\) 的整块(即 \(\tt *0\ldots 0\sim *1\ldots 1\))后的 \(x'\bmod 64\) 和所需操作次数,转移是简单的,至于 \(f_{i,s,0}\) 和 \(g_{i,s,0}\) 可以直接暴力计算。现在计算 \(x\) 重复操作直到 \(\gt L\) 时的真值以及操作次数,可以先补齐高位末尾的 \(0\) 再逼近到 \(\lfloor L/64\rfloor-1\),最后一个散块直接暴力即可。
对于 \(n>1\) 的情况,考虑计算每个值两两之间的 LCA 再容斥计算。具体地,LCA 可以通过判断操作到 \(>k\) 的真值是否相同直接二分答案实现。这样朴素实现可以做到 \(O(n^2\log^2V)\),因为 \(\max w\) 和 \(\log V\) 同阶。
不难发现,对于若干个值让他们同时逼近到某个大于他们最大值的值 \(k\),最后得到的最多只有 \(\max w\) 个不同的值,因此, 将 \(a\) 排序,从左至右遍历,每次让所有候选值逼近 \(a_i-1\),直到超过它。这样就可以做到 \(O(n\log^3 V)\) 了。
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
using ll=long long;
using ull=unsigned long long;
const int N=6e4+9;
const int B=62;
int w[64],n;
ll a[N],fa[N],f[64][64][64],g[64][64][64],lim;
inline void Init(){
for(int i=0;i<=B-6;i++){
for(int s=0;s<64;s++){
if(!i&&!s) continue ;
int cnt=0,x=s;
while(x<64){
cnt++;
x+=w[i+__builtin_popcountll(x)];
}
f[i][s][0]=x&63;
g[i][s][0]=cnt;
}
}
for(int k=1;k<=B-6;k++){
for(int i=0;i<=B-k-6;i++){
for(int s=0;s<64;s++){
f[i][s][k]=f[i+1][f[i][s][k-1]][k-1];
g[i][s][k]=g[i][s][k-1]+g[i+1][f[i][s][k-1]][k-1];
}
}
}
}
inline array<ll,2> F(ll x,ll lim){
ll i=x>>6,b=x&63,li=lim>>6,trg=li-1,cnt=0;
for(int k=0;k<=B;k++){
if(~i>>k&1) continue ;
if(i+(1ll<<k)>trg) continue ;
cnt+=g[__builtin_popcountll(i)][b][k];
b=f[__builtin_popcountll(i)][b][k];
i+=(1ll<<k);
}
for(int k=B;k>=0;k--){
if(i>>k&1) continue ;
if(i+(1ll<<k)>trg) continue ;
cnt+=g[__builtin_popcountll(i)][b][k];
b=f[__builtin_popcountll(i)][b][k];
i+=(1ll<<k);
}
x=i<<6|b;
while(x<=lim){
cnt++;
x+=w[__builtin_popcountll(x)];
}
return {cnt,x};
}
inline ll LCA(ll x,ll y){
if(x>y) swap(x,y);
if(F(x,y-1)[1]==y) return y;
ll sum=0;
for(int k=B;k>=0;k--){
if(F(x,sum|(1ll<<k))[1]!=F(y,sum|(1ll<<k))[1]){
sum|=(1ll<<k);
}
}
x=F(x,sum)[1],y=F(y,sum)[1];
if(x>y) swap(x,y);
return x+w[__builtin_popcountll(x)];
}
signed main(){
cin.tie(0),cout.tie(0);
ios::sync_with_stdio(0);
cin>>n>>lim;
for(int i=1;i<=B;i++) cin>>w[i];
for(int i=1;i<=n;i++) cin>>a[i];
Init();
ll sum=0;
vector<ll> cur;
sort(a+1,a+n+1);
for(int i=1;i<=n;i++){
vector<ll> lft;
for(ll x:cur){
ll f=LLONG_MAX;
for(ll y:cur){
if(y==x) break ;
if(F(x,a[i]-1)[1]!=F(y,a[i]-1)[1]) continue ;
f=min(f,LCA(x,y));
}
auto tmp=F(x,a[i]-1);
sum+=tmp[0];
if(f!=LLONG_MAX){
auto pmt=F(f,a[i]-1);
sum-=pmt[0];
}
lft.push_back(F(x,a[i]-1)[1]);
}
lft.push_back(a[i]);
sort(lft.begin(),lft.end());
lft.erase(unique(lft.begin(),lft.end()),lft.end());
cur=lft;
}
for(ll x:cur){
ll f=LLONG_MAX;
for(ll y:cur){
if(y==x) break ;
if(F(x,lim)[1]!=F(y,lim)[1]) continue ;
f=min(f,LCA(x,y));
}
auto tmp=F(x,lim);
sum+=tmp[0];
if(f!=LLONG_MAX){
auto pmt=F(f,lim);
sum-=pmt[0];
}
}
cout<<sum<<endl;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号