[ABC365] F - Takahashi on Grid

题解

容易发现题目中的一段连续的区间可以分为两类：

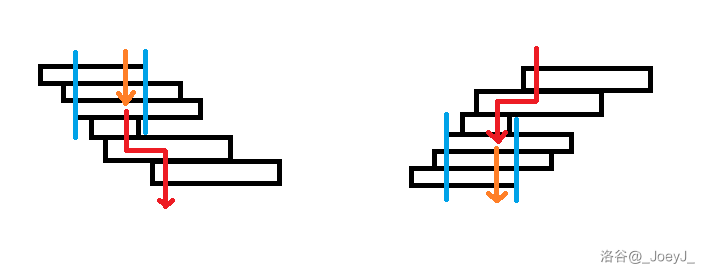
• 区间有交，可以一路到底的：

  

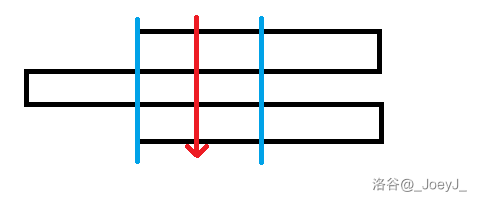
• 区间无交，需要绕路的：

  

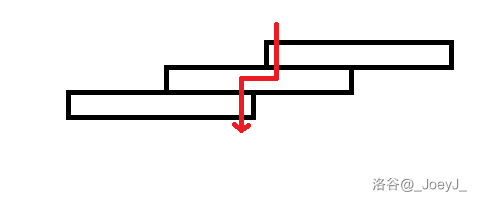
对于这两类连续段，我们考虑现在起点和终点分别在这段区间的首位两个区间时对答案的横向贡献：

• 区间有交时，若起点（终点）在区间中，则贡献为 \(0\)
  ，否则贡献为起点（终点）到该区间的最小距离。

• 区间无交时，我们先计算出通过这段区间的最短路的起点（终点），发现从起点（终点）先走到最短路的起点（终点）肯定不劣，所以直接计算起点（终点）走到最短路的起点（终点）的距离。

现在的问题在于如何合并区间信息并计算贡献，我们称区间有交的连续段为 A 类，区间无交的连续段为 B 类。显然单个区间均为 A 类连续段。合并可以分为以下几种情况：

• 合并 A 类连续段和 A 类连续段。若合并后区间仍有交集，则合并后仍然是 A 类连续段，合并的贡献为 \(0\)。否则合并后为 B 类连续段，贡献增加两个区间的最短路的距离。

  

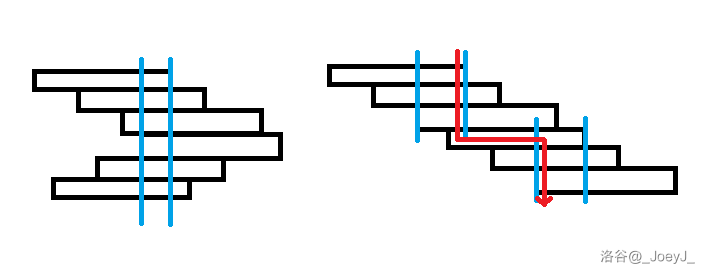
• 合并 B 类连续段和 B 类连续段。这是简单的，合并后仍然是 B 类连续段，贡献增加前面连续段最短路的终点和后面连续段最短路起点的距离。

  

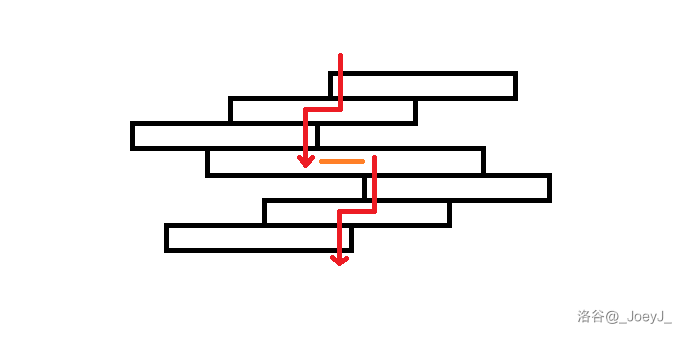
• 合并 A 类连续段和 B 类连续段。若 B 类连续段端点在 A 类连续段中，则合并的贡献为 \(0\)，否则贡献为端点到 A 类连续段区间交的最短路。

  

最后加上纵向贡献和起点与终点的横向贡献就可以了。

代码

信息合并，typ=0 是 A 类，typ=1 是 B 类。

struct Seg{
    int l,r,typ,w;
    pair<int,int> st,ed;
    Seg(){}
    Seg(int a,int b){l=a;r=b;typ=0;st=ed={a,b};}
    Seg(int a,int b,pair<int,int> c,pair<int,int> d,int wr,int t){l=a;r=b;typ=t;st=c;ed=d;w=wr;}
    Seg operator +(Seg x){
        if(typ==-1||x.typ==-1) return Seg(0,0,{0,0},{0,0},inf,-1);
        if(max(ed.first,x.st.first)>min(ed.second,x.st.second)) return Seg(0,0,{0,0},{0,0},inf,-1);
        if(typ){
            if(x.typ){
                return Seg(l,x.r,st,x.ed,w+x.w+abs(r-x.l),1);
            }else{
                if(r<x.l) return Seg(l,x.l,st,x.ed,w+x.w+abs(r-x.l),1);
                else if(r>x.r) return Seg(l,x.r,st,x.ed,w+x.w+abs(r-x.r),1);
                else return Seg(l,r,st,x.ed,w+x.w,1);
            }
        }else{
            if(x.typ){
                if(l>x.l) return Seg(l,x.r,st,x.ed,w+x.w+abs(l-x.l),1);
                else if(r<x.l) return Seg(r,x.r,st,x.ed,w+x.w+abs(r-x.l),1);
                else return Seg(x.l,x.r,st,x.ed,w+x.w,1);
            }else{
                if(l>x.r) return Seg(l,x.r,st,x.ed,w+x.w+abs(l-x.r),1);
                else if(r<x.l) return Seg(r,x.l,st,x.ed,w+x.w+abs(r-x.l),1);
                else return Seg(max(l,x.l),min(r,x.r),st,x.ed,w+x.w,0);
            }
        }
    }
};

int s,t,a,b;
cin>>s>>a>>t>>b;
if(s>t) swap(s,t),swap(a,b);
Seg res=Query(1,s,t);
if(res.typ==-1) cout<<-1<<endl;
else{
    int ans=res.w+abs(s-t);
    if(res.typ) ans+=abs(a-res.l)+abs(b-res.r);
    else{
        if(a<res.l&&b<res.l||a>res.r&&b>res.r) ans+=min(abs(a-res.l),abs(a-res.r))+min(abs(b-res.l),abs(b-res.r));
        else ans+=abs(a-b);
    }
  cout<<ans<<endl;
}