dp

0-1背包问题

给定n个重量为w1
w1​，w2w2​,w3w3​,…,wnwn​，价值为v1v1​,v2v2​,v3v3​,…,vnvn​的物品和容量为CC的背包，求这个物品中一个最有价值的子集，使得在满足背包的容量的前提下，包内的总价值最大

代码

#include<iostream>
#include<cstring>
#include<algorithm>
#define maxn 110
using namespace std;
int f[maxn][maxn],w[maxn],v[maxn],n,W;
int solve(int x,int res)//序号和剩余的重量，没必要写多个参数，会使记忆化很难实现
{
    int k;
    if(f[x][res]>=0) return f[x][res];//已选择
    if(x==n) k= 0;//排到头
    else if(res<w[x])
        k=solve(x+1,res);//不够，看看下一个是否可以
    else
    {
        k= max(solve(x+1,res),solve(x+1,res-w[x])+v[x]);//选他和不选他的大小比较
    }
    return f[x][res]=k;//记忆化搜索，记录结果，标志
}
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>w[i]>>v[i];
    cin>>W;
    memset(f,-1,sizeof(f));
    cout<<solve(0,W)<<endl;
}
优化：动态规划，（从记忆化搜索导出递推式，实现动态规划

#include<iostream>
#include<cstring>
#include<algorithm>
#define maxn 110
using namespace std;
int f[maxn][maxn],w[maxn],v[maxn],n,W;
int main()//根据上述代码，得出递推公式，进而优化
{
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>w[i]>>v[i];
    cin>>W;
    memset(f,0,sizeof(f));
    for(int i=n-1;i>=0;i--)//这里是已知f[n][0]=0,根据递推公式知道后面的，求前面的
    {
        for(int j=0;j<=W;j++)//这个地方需要循环到W，因为可以取w
        {
            if(j<w[i])
                f[i][j]=f[i+1][j];
            else
            {
                f[i][j]=max(f[i+1][j],f[i+1][j-w[i]]+v[i]);
            }
        }
    }
    cout<<f[0][W]<<endl;
}
二、最长子序列

给定两个序列长度N和M，给出X = <x1，x2，...，xm>和Y = <y1，y2，...，yn>，求X和Y长度最长的公共子序列。

 

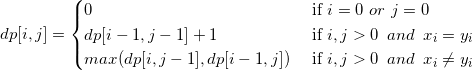
 代码：
#include<iostream>
#include<algorithm>
#include<cstring>
#define maxn 1010
using namespace std;
int N,M;
int s[maxn][maxn];
string a,b;
int main()
{
    while(cin>>N>>M)
    {
        for(int i=0;i<N;i++)
            cin>>a[i];
        for(int i=0;i<M;i++)
            cin>>b[i];
        memset(s,0,sizeof(s));
        for(int i=0;i<N;i++)
        {
            for(int j=0;j<M;j++)
            {
                if(a[i]==b[j])
                    s[i+1][j+1]=s[i][j]+1;
                else
                    s[i+1][j+1]=max(s[i][j+1],s[i+1][j]);
            }
        }
        cout<<s[N][M]<<endl;
    }
    return 0;
}