并查集基础

目录

• 并查集
  • 算法介绍
  • 基本操作
  • 路径压缩和按秩合并
  • 使用方法
    • 维护无向图中节点连通性
    • 快速跳过无用集合
  • 例题
    • 程序自动分析
    • Supermarket
• 边带权 并查集
  • 算法介绍
  • 例题
    • 银河英雄传说
    • Parity game
• 扩展域 并查集
  • 算法介绍
  • 例题 Parity game
  • 练习题 食物链
• 习题
  • 信息传递
  • 修复公路
  • 【模板】并查集
  • 奶酪

并查集

算法介绍

并查集是一种树形的数据结构，用于处理不相交集合间的合并及查询问题

在使用中常以 森林 来表示

集合定义方法：“代表元法”，即 每个集合选择一个固定的元素，作为整个集合的 “代表” 元素

基本操作

• 初始化：将元素 \(x\) 作为自身集合的 “代表” 元素

  for(int i = 1; i <= n; ++ i) fa[i] = i; 
  

• \(find(x)\)：查询元素 \(x\) 所在集合的 “代表” 元素

  int find(int x) {
  	if(x == fa[x]) return x;
  	return find(fa[x]);
  }
  

• \(merge(x, y)\)：合并元素 \(x, y\) 所在的两个集合

  void merge(int x, int y) {
  	int fx = fa[x], fy = find(y);
  	if(fx == fy) return;
  	fa[fx] = fy;
  }
  

路径压缩和按秩合并

• 路径压缩，均摊时间复杂度 \(O(logN)\)

  \(find(x)\) 时，将 \(x\) 的 父节点 直接指向 根节点（“代表” 元素）

  适用情况：题目中不需要维护明确的父子关系

  int find(int x) { return x == fa[x] ? fa[x] : fa[x] = find(fa[x]); }
  

• 按秩合并，均摊时间复杂度 \(O(logN)\)

  “秩”：树的深度 / 集合大小

  将 “秩” 记录在代表元素。合并时，将 “秩” 较小的树根作为 “秩” 较大的树根的子节点

  void merge(int x, int y) {	//按大小合并 
  	int fx = find(x), fy = find(y);
  	if(fx == fy) return;
  	if(siz[fx] < siz[fy]) fa[fx] = fy, siz[fy] += siz[fx];
  	else fa[fy] = fx, siz[fx] += siz[fy];
  }
  

  void merge(int x, int y) {	//按深度合并 
  	int fx = find(x), fy = find(y);
  	if(fx == fy) return;
  	if(high[fx] < high[fy]) fa[fx] = fy;
  	if(high[fx] > high[fy]) fa[fy] = fx;
  	if(high[fx] == high[fy]) fa[fx] = fy, high[fy] ++;
  }
  

注意：

• 实际使用时，常常只使用路径压缩过的并查集

  只有当需要考虑到节点间父子关系或追求程序运行效率（题目一般不会卡路径压缩的做法）时

  才会用到按秩合并

• 同时采用 路径压缩 和 按秩合并 优化的并查集，每次 \(find(x)\) 时间复杂度可降低到 \(O(\alpha(N))\)

  即为 反阿克曼函数

使用方法

维护无向图中节点连通性

给定一张 \(n\)个点、\(m\) 条边的无向图

\(q\) 次询问，每次询问点 \(x, y\) 是否处于同一连通块

\(1\leq n\leq 10^5,1\leq m,q\leq 10^6\)

使用并查集的基本操作即可

当 \(x,y\) 间存在一条边时，对 \(x,y\) 所在集合进行合并

查询时，查看 \(x,y\) 两点所在集合的 “代表” 元素是否相同即可

注：实际上，并查集可以用于维护许多具有传递性的关系

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int read() {
	int x = 0, f = 1; char ch;
	while(! isdigit(ch = getchar())) (ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 3) + (x << 1) + (ch ^ 48));
	return x * f;
}
template <class T> T Max(T a, T b) { return a > b ? a : b; }
template <class T> T Min(T a, T b) { return a < b ? a : b; }
int fa[N]; 
int find(int x) { return x == fa[x] ? fa[x] : fa[x] = find(fa[x]); }
int main() {
	int n = read(), m = read();
	for(int i = 1, x, y; i <= m; ++ i) {
		x = read(); y = read();
		int fx = find(x), fy = find(fy);
		fa[fx] = fy;
	}
	int q = read();
	for(int i = 1, x, y; i <= q; ++ i) {
		x = read(); y = read();
		int fx = find(x), fy = find(y);
		printf(fx == fy ? "Yes\n" : "No");
	}
	return 0;
}

快速跳过无用集合

BZOJ2054 疯狂的馒头

\(n\) 个白色的馒头，\(m\)次染色操作

第 \(i\) 次染色操作将第 \((i*p+q)\ mod\ n + 1\) 个馒头和第 \((i*q+p)\ mod\ n+1\)个馒头之间馒头染成颜色 \(i\)

输出每个馒头最终被染成的颜色

\(1\leq n\leq 10^6,1\leq m\leq 10^7\)，时限 \(10s\)

题解：

每个馒头最终被染成的颜色只和最后一次染色有关系

考虑倒叙枚举染色操作

则每个馒头第一次被染成的颜色（实际为最后一次）即为最终颜色

暴力的时间复杂度为 \(O(n*m)\)

考虑到在枚举染色区间时，每个馒头可能被无效枚举若干次（已经被确定最终颜色）

使用并查集对已染色的馒头区间进行压缩

时间复杂度：\(O(m*lgn)\)

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int read() {
	int x = 0, f = 1; char ch;
	while(! isdigit(ch = getchar())) (ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 3) + (x << 1) + (ch ^ 48));
	return x * f;
}
template <class T> T Max(T a, T b) { return a > b ? a : b; }
template <class T> T Min(T a, T b) { return a < b ? a : b; }
int c[N], fa[N]; 
int find(int x) { return x == fa[x] ? fa[x] : fa[x] = find(fa[x]); }
int main() {
	int n = read(), m = read(), p = read(), q = read();
	for(int i = 1; i <= n + 1; ++ i) fa[i] = i; 
	for(int i = m, x, y; i >= 1; -- i) {
		x = (i * p % n + q) % n + 1;
		y = (i * q % n + p) % n + 1;
		if(x > y) swap(x, y);
		for(int j = find(x); j <= y; j = find(j)) {
			c[j] = i; fa[j] = j + 1;
		}
	}
	for(int i = 1; i <= n; ++ i) printf("%d\n", c[i]);
	return 0;
}

例题

程序自动分析

题目链接：P1955 [NOI2015] 程序自动分析

给定 \(n\) 行约束条件，每行 \(3\) 个整数 \(i,j,e\)

若 \(e=1\)，说明 \(x_i=x_j\)

若 \(e=0\)，说明 \(x_i\neq x_j\)

判定这些约束条件能否被同时满足

\(T\) 组数据

\(1\leq T\leq 10，1\leq i,j\leq 10^9,1\leq n\leq10^6\)

题解：

根据题意，可能会被用到的变量最多只有 \(2*n\) 个

所以，首先对变量下标进行离散化操作

对约束条件进行排序，优先考虑 \(e=1\) 的情况

利用并查集将相同的变量元素维护在同一连通块内

当考虑 \(e=0\) 的情况时，若存在 \(x_i\) 和 \(x_j\) 处于同一连通块，则该约束条件不可被满足

否则所有约数条件可同时被满足

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e6 + 5;
typedef long long LL;
int read() {
	int x = 0, f = 1; char ch;
	while(! isdigit(ch = getchar())) (ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 3) + (x << 1) + (ch ^ 48));
	return x * f;
}
template <class T> T Max(T a, T b) { return a > b ? a : b; }
template <class T> T Min(T a, T b) { return a < b ? a : b; }
int tot, fa[N], b[N];
struct node { int i, j, e; } p[N];
bool cmp_e(node x, node y) { return x.e > y.e; }
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
void solve() {
	tot = 0;
	int n = read();
	for(int i = 1; i <= n; ++ i) p[i].i = read(), p[i].j = read(), p[i].e = read();
	for(int i = 1; i <= n; ++ i) b[++ tot] = p[i].i, b[++ tot] = p[i].j;
	sort(b + 1, b + tot + 1);
	tot = unique(b + 1, b + tot + 1) - (b + 1); 
	for(int i = 1; i <= n; ++ i) {
		p[i].i = lower_bound(b + 1, b + tot + 1, p[i].i) - b;
		p[i].j = lower_bound(b + 1, b + tot + 1, p[i].j) - b;
	}
	for(int i = 1; i <= tot; ++ i) fa[i] = i;
	sort(p + 1, p + n + 1, cmp_e);
	for(int i = 1; i <= n; ++ i) {
		int fx = find(p[i].i), fy = find(p[i].j);
		if(p[i].e) fa[fx] = fy;
		else if(fx == fy) return printf("NO\n"), (void)0;
	}
	printf("YES\n"); 
}
int main() {
	int T = read();
	while(T --> 0) solve();
	return 0;
}

Supermarket

题目链接：UVA1316 Supermarket

给定 \(n\) 件物品，第 \(i\) 件物品有如下信息：

• 卖出去可以得到 \(p_i\) 的收益
• 过期时间为 \(d_i\)，过期后就不能再卖出去

卖掉一件物品要用 \(1\) 的时间，求最大收益

多组数据，每组数据一行。首先是一个整数 \(n\)，然后是 \(n\) 对数 \(p_i,d_i\)，以文件终止符结束

\(0\leq n\leq10^4,1\leq p_i,d_i\leq10^4\)

题解：

每个时间只能卖出一件物品

考虑有限时间内尽量卖出收益高的物品

将物品按 \(p_i\) 从大到小排序

每件物品应在过期前尽量晚卖出，满足贪心的 “决策包容性”

建立关于 "时间" 元素 的并查集，维护 每个时间的占用情况

当一件物品决定在时间 \(day\) 被卖出后，利用并查集将时间 \(day\) 合并到 \(day-1\) 上

帮助快速查找某个时间之前 还未决定卖出物品的第一个时间

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e6 + 5;
typedef long long LL;
int read() {
	int x = 0, f = 1; char ch;
	while(! isdigit(ch = getchar())) (ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 3) + (x << 1) + (ch ^ 48));
	return x * f;
}
template <class T> T Max(T a, T b) { return a > b ? a : b; }
template <class T> T Min(T a, T b) { return a < b ? a : b; }
int n, fa[N];
struct node { int p, d; } e[N];
bool cmp(node x, node y) { return x.p > y.p; }
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
void solve() {
	int mx = 0, ans = 0;
	for(int i = 1; i <= n; ++ i) e[i].p = read(), mx = max(mx, e[i].d = read());
	sort(e + 1, e + n + 1, cmp);
	for(int i = 1; i <= mx; ++ i) fa[i] = i;
	for(int i = 1; i <= n; ++ i) {
		int day = find(e[i].d);
		if(day == 0) continue;
		ans += e[i].p;
		fa[day] = find(day - 1);
	}
	printf("%d\n", ans);
}
int main() {
	while(scanf("%d", &n)) solve();
	return 0;
}

边带权 并查集

算法介绍

由于并查集能够维护很多具有传递性的关系，且并查集总是呈树形结构

因此可以用数组在每个节点处记录该节点与其父亲节点之间的关系

在路径压缩过程中，及时正确修改关系值即可

例题

银河英雄传说

题目链接：P1196 [NOI2002] 银河英雄传说

初始时，共 \(30000\) 个战舰，第 \(i\) 号战舰处于第 \(i\) 列

共 \(n\) 条指令，每条指令占一行，共两种指令，格式如下：

• \(M\ i\ j\)：将 \(i\) 号所在战舰队列作为整体接至 \(j\) 号所在战舰队列尾部

• \(C\ i\ j\)： 判断 \(i\) 号战舰和 \(j\) 号战舰是否在同一列

若在同一列，则输出它们之间战舰的个数，否则输出 \(-1\)

\(1\leq n\leq 5*10^5,1\leq i,j\leq 30000\)

题解：

若只是判断两战舰是否在同一列，仅使用普通并查集即可

题目中还需要维护两战舰之间的战舰个数

定义如下变量：

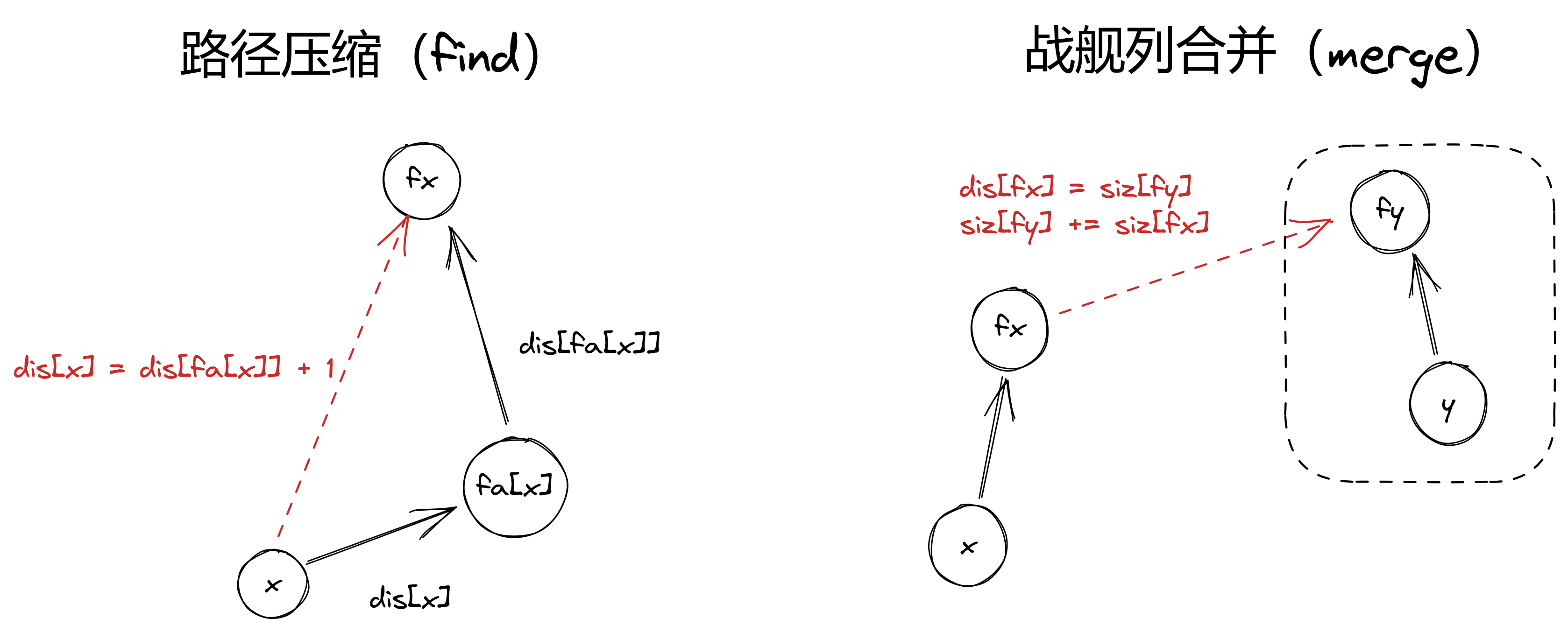
• \(dis[x]\)：\(x\) 前面有多少战舰（不包括 \(x\)）
• \(siz[x]\)：\(x\) 所在战舰列的战舰个数（仅在根节点维护正确值，用于合并两集合时对 \(dis\) 进行更新）

在 \(find\) 和 \(merge\) 时对信息进行维护即可

若 \(x\) 和 \(y\) 处于同一战舰列，两战舰之间的战舰个数为 \(Abs(dis[x]-dis[y])-1\)

​

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 3e4 + 5;
typedef long long LL;
int read() {
	int x = 0, f = 1; char ch;
	while(! isdigit(ch = getchar())) (ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 3) + (x << 1) + (ch ^ 48));
	return x * f;
}
template <class T> T Max(T a, T b) { return a > b ? a : b; }
template <class T> T Min(T a, T b) { return a < b ? a : b; }
int Abs(int x) { return x > 0 ? x : -x; }
char c[5];
int n, fa[N], dis[N], siz[N];
int find(int x) {
	if(x == fa[x]) return x;
	int fx = find(fa[x]);
	dis[x] += dis[fa[x]];
	return fa[x] = fx;
}
void merge(int x, int y) {
	int fx = find(x), fy = find(y);
	fa[fx] = fy; dis[fx] = siz[fy];
	siz[fy] += siz[fx];
}
void query(int x, int y) {
	int fx = find(x), fy = find(y);
	if(fx != fy) return printf("-1\n"), (void)0;
	printf("%d\n", Abs(dis[x] - dis[y]) - 1);
}
int main() {
	n = read();
	for(int i = 1; i <= 3e4; ++ i) fa[i] = i, siz[i] = 1;
	for(int i = 1, x, y; i <= n; ++ i) {
		scanf("%s", c + 1);
		x = read(); y = read();
		if(c[1] == 'M') merge(x, y);
		if(c[1] == 'C') query(x, y);
	}
	return 0;
}

Parity game

题目链接：P5937 [CEOI1999]Parity Game

一个长度为 \(n\) 的 \(01\) 序列 \(s\)，给出 \(m\) 条判断信息

每行信息格式为两个整数 \(x,y\) 和一个字符串

若字符串为 \(even\)，表示区间 \(s[x,y]\) 中 \(1\) 的个数为偶数个

若字符串为 \(odd\)，表示区间 \(s[x,y]\) 中 \(1\) 的个数为奇数个

输出一个数 \(k\)，满足前 \(k\) 组信息是正确的的前提下，第 \(k+1\) 组信息是错的

若判断信息全部正确，则输出 \(m\)

\(1\leq n\leq 10^9,1\leq m\leq 5000\)

题解：

用 \(sum\) 表示序列 \(s\) 的前缀和

• \(s[l,r]\) 有偶数个 \(1\) 等价于 \(sum[l-1]\) 与 \(sum[r]\) 奇偶性相同

• \(s[l,r]\) 有奇数个 \(1\) 等价于 \(sum[l-1]\) 与 \(sum[r]\) 奇偶性相反

由于序列很长，需要先对 \(l-1\) 和 \(r\) 进行离散化

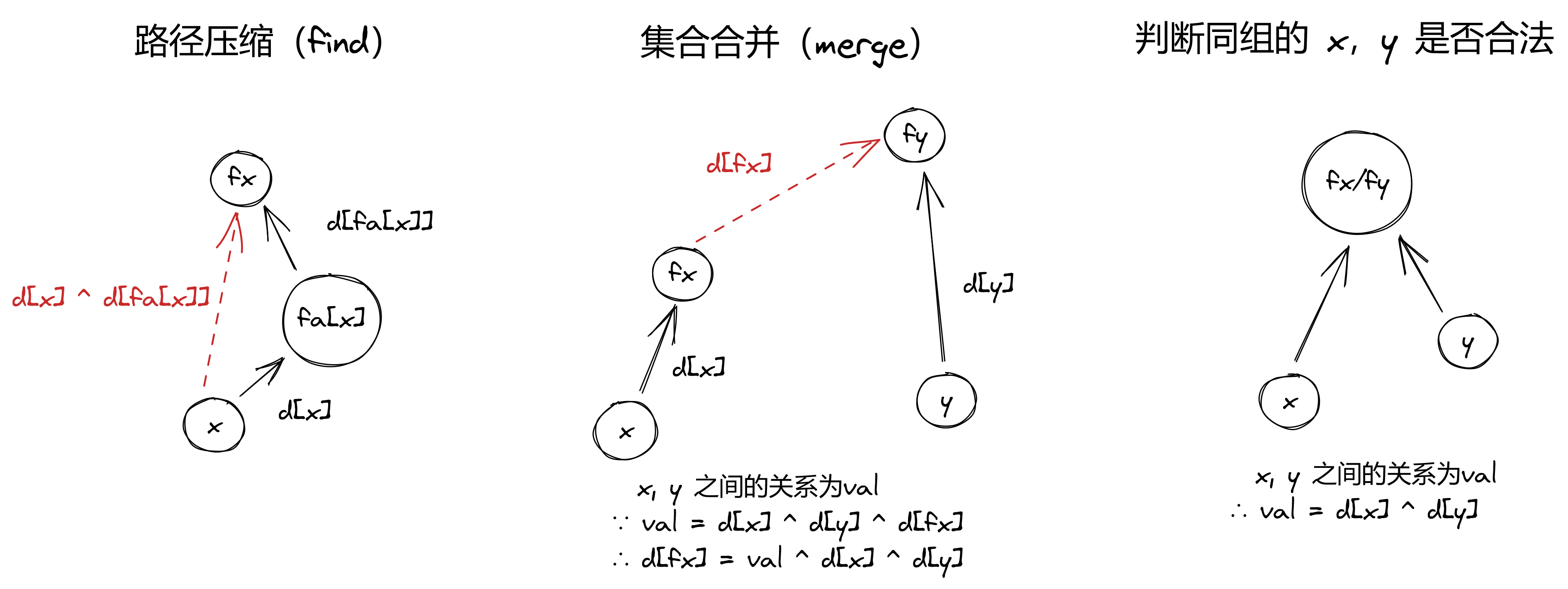
利用并查集维护奇偶性关系

设 \(d[x]\) 表示奇偶性关系

• \(d[x]=0\)，表示 \(x\) 与 \(fa[x]\) 的奇偶性相同

• \(d[x]=1\)，表示 \(x\) 与 \(fa[x]\) 的奇偶性相反

可以通过巧妙的异或运算对 \(d[x]\) 进行维护

若 A ^ B = C，那么有 C ^ A = B，C ^ B = A

对于多个数的情况，该性质仍然成立

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int read() {
	int x = 0, f = 1; char ch;
	while(! isdigit(ch = getchar())) (ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 3) + (x << 1) + (ch ^ 48));
	return x * f;
}
template <class T> T Max(T a, T b) { return a > b ? a : b; }
template <class T> T Min(T a, T b) { return a < b ? a : b; }
char s[5];
struct node { int l, r, val; } q[N];
int tot, b[N], fa[N], d[N];
int find(int x) {
	if(x == fa[x]) return x;
	int fx = find(fa[x]);
	d[x] ^= d[fa[x]];
	return fa[x] = fx;
}
int main() {
	int n = read(), m = read();
	for(int i = 1; i <= m; ++ i) {
		q[i].l = read() - 1; q[i].r = read();
		scanf("%s", s + 1);
		q[i].val = (s[1] == 'o' ? 1 : 0);
		b[++ tot] = q[i].l;
		b[++ tot] = q[i].r;
	}
	sort(b + 1, b + tot + 1);
	n = unique(b + 1, b + tot + 1) - (b + 1);
	for(int i = 1; i <= n; ++ i) fa[i] = i;
	for(int i = 1; i <= m; ++ i) {
		int x = lower_bound(b + 1, b + n + 1, q[i].l) - b;
		int y = lower_bound(b + 1, b + n + 1, q[i].r) - b;
		int fx = find(x), fy = find(y);
		if(fx == fy) {
			if((d[x] ^ d[y]) != q[i].val) return printf("%d\n", i - 1), 0;
		}
		else {
			fa[fx] = fy;
			d[fx] = d[x] ^ d[y] ^ q[i].val;
		}
	}
	printf("%d\n", m);
	return 0;
}

扩展域 并查集

算法介绍

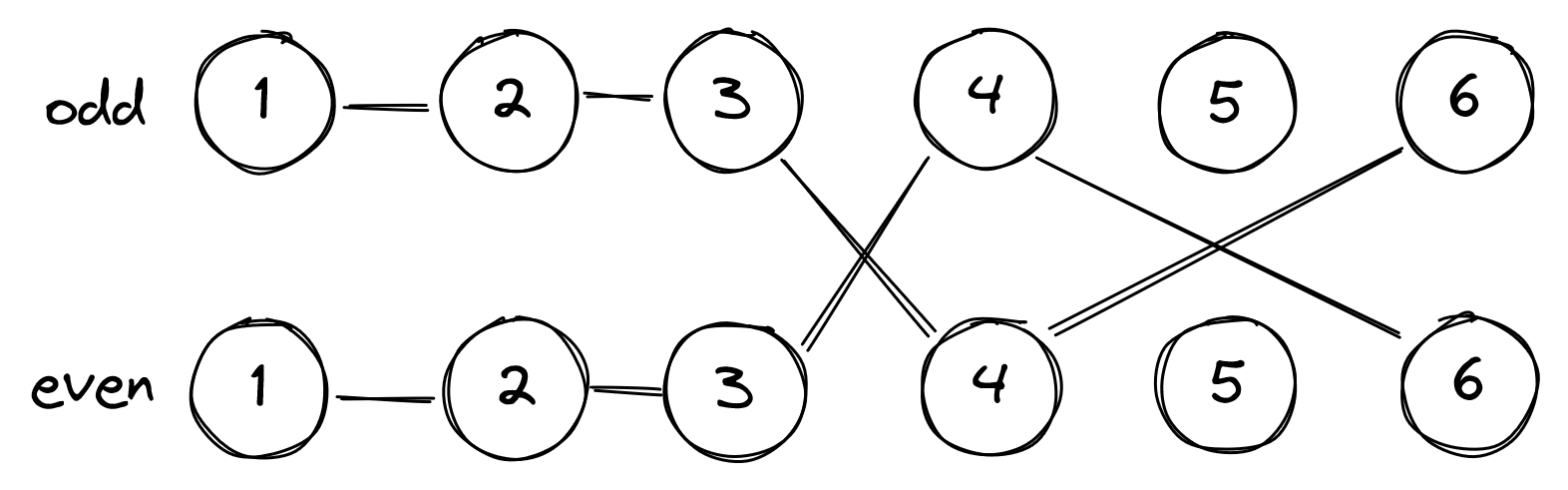
当并查集所维护的元素具有若干不同时存在的性质时，考虑拆点思想

若元素 \(x\) 存在 \(op\) 种性质，则将 \(x\) 拆成 \(op\) 个点

再根据题目中的条件，对有关系的点对进行连接

再根据连通性对题目进行判断

例题 Parity game

题目链接：P5937 [CEOI1999]Parity Game

一个长度为 \(n\) 的 \(01\) 序列 \(s\)，给出 \(m\) 条判断信息

每行信息格式为两个整数 \(x,y\) 和一个字符串

若字符串为 \(even\)，表示区间 \(s[x,y]\) 中 \(1\) 的个数为偶数个

若字符串为 \(odd\)，表示区间 \(s[x,y]\) 中 \(1\) 的个数为奇数个

输出一个数 \(k\)，满足前 \(k\) 组信息是正确的的前提下，第 \(k+1\) 组信息是错的

若判断信息全部正确，则输出 \(m\)

\(1\leq n\leq 10^9,1\leq m\leq 5000\)

题解：

用 \(sum\) 表示序列 \(s\) 的前缀和

• \(s[l,r]\) 有偶数个 \(1\) 等价于 \(sum[l-1]\) 与 \(sum[r]\) 奇偶性相同

• \(s[l,r]\) 有奇数个 \(1\) 等价于 \(sum[l-1]\) 与 \(sum[r]\) 奇偶性相反

由于序列很长，需要先对 \(l-1\) 和 \(r\) 进行离散化

利用扩展域并查集进行维护判断即可

将有关系的点对进行连接

根据点对的连通性判断信息是否合法

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int read() {
	int x = 0, f = 1; char ch;
	while(! isdigit(ch = getchar())) (ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 3) + (x << 1) + (ch ^ 48));
	return x * f;
}
template <class T> T Max(T a, T b) { return a > b ? a : b; }
template <class T> T Min(T a, T b) { return a < b ? a : b; }
char s[5];
struct node { int l, r, val; } q[N];
int tot, b[N], fa[N];
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
int main() {
	int n = read(), m = read();
	for(int i = 1; i <= m; ++ i) {
		q[i].l = read() - 1; q[i].r = read();
		scanf("%s", s + 1);
		q[i].val = (s[1] == 'o' ? 1 : 0);
		b[++ tot] = q[i].l;
		b[++ tot] = q[i].r;
	}
	sort(b + 1, b + tot + 1);
	n = unique(b + 1, b + tot + 1) - (b + 1);
	for(int i = 1; i <= 2 * n; ++ i) fa[i] = i;
	for(int i = 1; i <= m; ++ i) {
		int x = lower_bound(b + 1, b + n + 1, q[i].l) - b;
		int y = lower_bound(b + 1, b + n + 1, q[i].r) - b;
		int x_odd = x, x_even = x + n;
		int y_odd = y, y_even = y + n;
		int fx = find(x), fy = find(y);
		if(q[i].val == 0) {
			if(find(x_odd) == find(y_even)) return printf("%d\n", i - 1), 0;
			fa[find(x_odd)] = find(y_odd);
			fa[find(x_even)] = find(y_even);
		}
		if(q[i].val == 1) {
			if(find(x_odd) == find(y_odd)) return printf("%d\n", i - 1), 0;
			fa[find(x_odd)] = find(y_even);
			fa[find(x_even)] = find(y_odd);
		}
	}
	printf("%d\n", m);
	return 0;
}

练习题 食物链

题目链接：P2024 [NOI2001] 食物链

习题

信息传递

题目链接：P2661 [NOIP2015 提高组] 信息传递

修复公路

题目链接：P1111 修复公路

【模板】并查集

题目链接：P3367 【模板】并查集

奶酪

题目链接：P3958 [NOIP2017 提高组] 奶酪