Java 递归
Java 递归
定义
递归是一种针对使用简单循环难以编程实现的问题,提供优雅解决方案的技术。
使用递归即使用递归方法(recursive method)编程,递归方法是直接或间接调用自身的方法。递归是很有用的程序设计技术,在某些情况下,对于其他方法难以解决的问题,递归能给出直观、直接的简单解法。例如遍历某个路径下的所有文件,若路径下文件夹深度未知,就可使用递归来实现。
示例:计算阶乘
阶乘定义
- 0! = 1;
- n! = n * (n - 1)!(n > 0)。
递归思路
已知 0! = 1,1! = 1 * 0!,可通过递推求得任意 n 的阶乘。计算 n! 的问题可简化为计算 (n - 1)!,直到 n 递减为 0(基础情况)。
递归算法描述
if(n == 0)
return 1;
else
return n * factorial(n - 1);
完整代码
package com.recusive;
import java.math.BigInteger;
/**
* @author Jing61
*/
public class ComputerFactorial {
public static BigInteger factorial(int n) {
if(n == 0) return BigInteger.valueOf(1);
return factorial(n - 1).multiply(BigInteger.valueOf(n));
}
public static void main(String[] args) {
System.out.println(factorial(5));
}
}
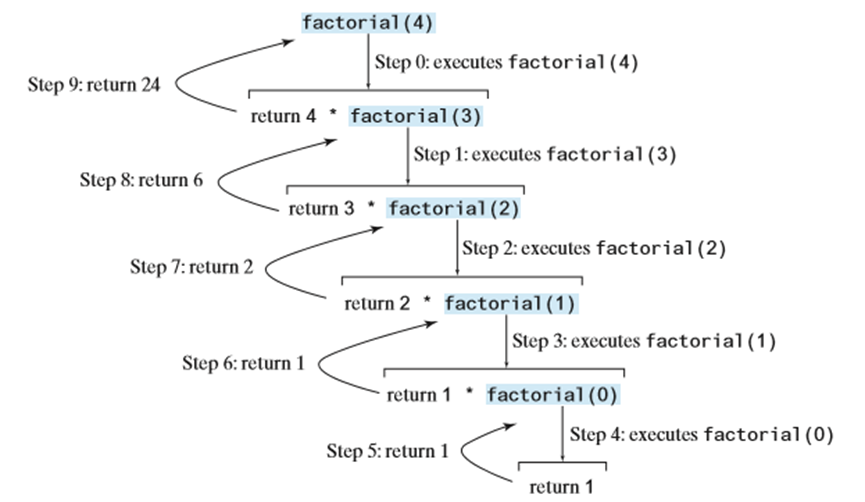
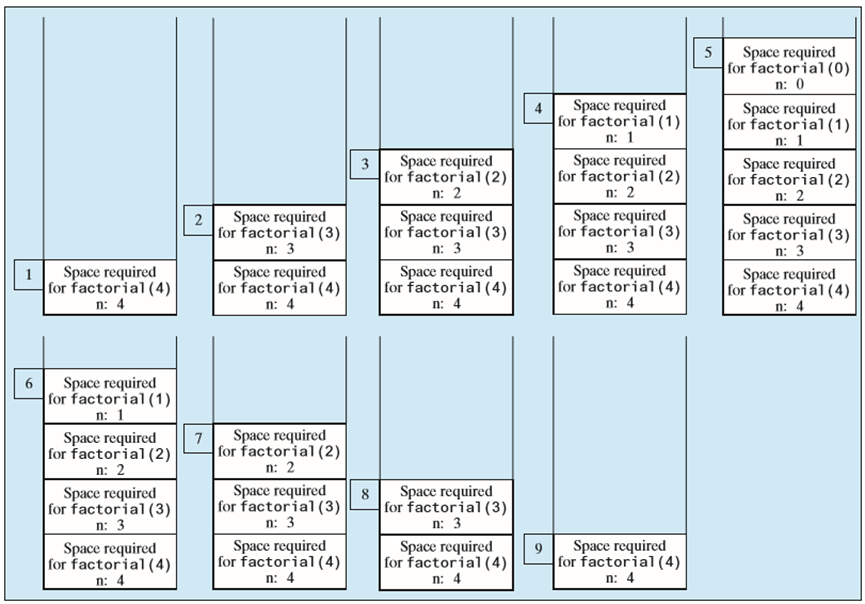
递归调用执行过程(以 n=4 为例)
- 执行 factorial(4),需计算 4 * factorial(3)
- 执行 factorial(3),需计算 3 * factorial(2)
- 执行 factorial(2),需计算 2 * factorial(1)
- 执行 factorial(1),需计算 1 * factorial(0)
- 执行 factorial(0),返回 1
- factorial(1) 返回 1 * 1 = 1
- factorial(2) 返回 2 * 1 = 2
- factorial(3) 返回 3 * 2 = 6
- factorial(4) 返回 4 * 6 = 24
![image]()
注意事项
- 循环实现阶乘更简单高效,此处仅用于演示递归概念。
- 若递归未收敛到基础情况,会出现无限递归,最终导致 StackOverflowError。例如遗漏 n==0 的判断,直接返回 n * factorial(n - 1),那么这个方法会无限执行下去,最终导致一个StackOverflowError。
![image]()
示例:计算斐波拉契数
斐波拉契数列定义
- Fib[0] = Fib[1] = 1;
- Fib[n] = Fib[n – 1] + Fib[n – 2](n ≥ 2)。
递归思路
已知 Fib[0] 和 Fib[1],可递推求得任意索引的斐波拉契数。计算 Fib(index) 的问题简化为计算 Fib(index-1) 和 Fib(index-2),直到 index 递减为 0 或 1(基础情况)。
完整代码
package com.recusive;
/**
* @author Jing61
*/
public class Fib {
public static void main(String[] args) {
System.out.println(fib(10));
}
public static int fib(int n) {
if(n < 2) return 1;
return fib(n - 1) + fib(n - 2);
}
}
使用递归解决问题
所有递归方法的核心特点:
- 用 if-else 或 switch 语句区分不同情况;
- 包含一个或多个基础情况(最简单场景)用于终止递归;
- 每次递归调用简化原始问题,使其不断接近基础情况,最终转化为基础情况。
递归解决问题的核心思路:将问题分解为与原始问题性质一致但规模更小的子问题,通过递归调用解决子问题。
示例 1:打印消息 n 次
问题分解
- 子问题 1:打印消息 1 次;
- 子问题 2:打印消息 n-1 次(与原始问题一致,规模更小)。
完整代码
package com.recusive;
public class RecursiveDemo {
public static void printN(int times, String message) {
if(times > 0) {
System.out.println(message);
printN(times - 1, message);
}
}
public static void main(String[] args) {
printN(5, "hello world");
}
}
示例 2:检查字符串是否为回文串
问题分解
- 子问题 1:检查字符串首尾字符是否相等;
- 子问题 2:忽略首尾字符,检查剩余子串是否为回文串(规模更小)。
完整代码
package com.recusive;
public class RecursiveDemo {
/**
* 判断字符串是否是回文
* 递归思路:递归判断字符串的起始索引和结束索引的字符是否相等,
* 如果相等,则继续递归判断字符串的起始索引加1和结束索引减1的字符是否相等,
* 直到起始索引和结束索引相等或者起始索引大于结束索引。
* @param s 字符串
* @param low 字符串的起始索引
* @param high 字符串的结束索引
* @return 首尾索引的字符是否相等,相等递归判断下一个,否则返回false
*/
public static boolean isPalindrome(String s, int low, int high) {
if(low >= high) return true;
return s.charAt(low) == s.charAt(high) && isPalindrome(s, low + 1, high - 1);
}
public static boolean isPalindrome(String s) {
return isPalindrome(s, 0, s.length() - 1);
}
public static void main(String[] args) {
System.out.println(isPalindrome("abcdcba"));
}
}
示例 3:递归选择排序
核心思路
- 找出列表中的最小元素,与第一个元素交换;
- 忽略第一个元素,对剩余子列表递归排序;
- 基础条件:列表仅包含一个元素。
完整代码
package com.recusive;
/**
* @author Jing61
* 递归选择排序
* 1、找出列表中的最小元素,然后将它和第一个元素进行交换
* 2、忽略第一个元素,对余下的较小的一些列表进行递归排序
* 基础条件:列表只包含一个元素
*/
public class RecursiveSelectionSort {
public static void main(String[] args) {
int[] arr = {5, 4, 3, 2, 1};
selectionSort(arr, 0);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
public static void selectionSort(int[] arr, int low) {
if(low >= arr.length) return;
int minIndex = low;
for (int i = low; i < arr.length; i++) {
if(arr[i] < arr[minIndex]) {
minIndex = i;
}
}
int temp = arr[minIndex];
arr[minIndex] = arr[low];
arr[low] = temp;
selectionSort(arr, low + 1);
}
}
示例 4:递归二分查找
前提条件
列表为有序数组。
核心思路
- 计算中间索引 mid,比较 list[mid] 与目标值 key;
- 若 list[mid] == key,返回 mid;
- 若 list[mid] > key,递归查找左子数组;
- 若 list[mid] < key,递归查找右子数组;
- 基础条件:左索引 > 右索引,返回 -1(未找到)。
完整代码
package com.recusive;
/**
* 二分查找前提:list是一个有序数组
* @author Jing61
*/
public class RecursiveBinarySearch {
public static void main(String[] args) {
int[] list = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
System.out.println(binarySearch(list, 0, list.length - 1, 5));
}
public static int binarySearch(int[] list, int left, int right, int key) {
if(left > right) return -1;
int mid = left + (right - left) / 2;
if(list[mid] == key) return mid;
else if(list[mid] > key) return binarySearch(list, left, mid - 1, key);
else return binarySearch(list, mid + 1, right, key);
}
}
示例 5:打印目录下所有文件名
核心思路
- 若当前文件是普通文件,直接打印文件名;
- 若当前文件是目录,遍历目录下所有子文件/子目录,递归调用打印方法。
完整代码
package com.recusive;
import java.io.File;
/**
* @author Jing61
*/
public class DirectoryName {
public static void printFileName(File file) {
if(file.isFile()) System.out.println(file.getName());
else if(file.isDirectory()) {
File[] files = file.listFiles();
for (File f : files) {
printFileName(f);
}
}
}
public static void main(String[] args) {
File file = new File("C:/Users/lenovo/Desktop/computer");
printFileName(file);
}
}
示例 6:汉诺塔问题
问题描述
- n 个盘子标记为 1 到 n,三个塔标记为 A、B、C;
- 任何时候盘子不能放在比它小的盘子上方;
- 初始状态所有盘子在塔 A 上,每次只能移动一个塔顶盘子;
- 目标:借助塔 C 将所有盘子从塔 A 移到塔 B。
n = 3 时
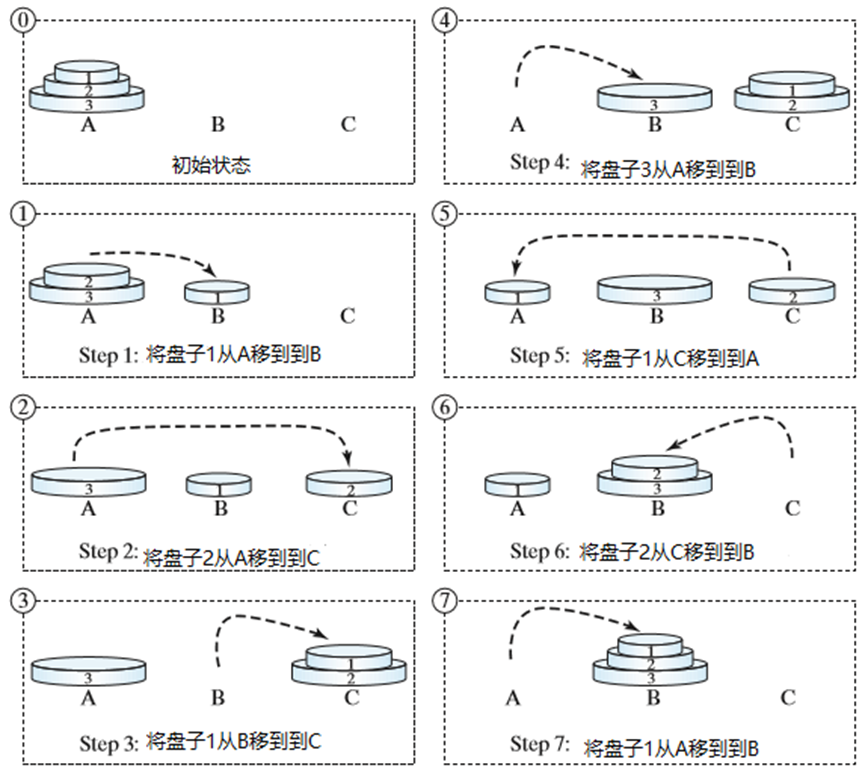
递归思路
- 基础情况:n=1 时,直接将盘子从 A 移到 B;
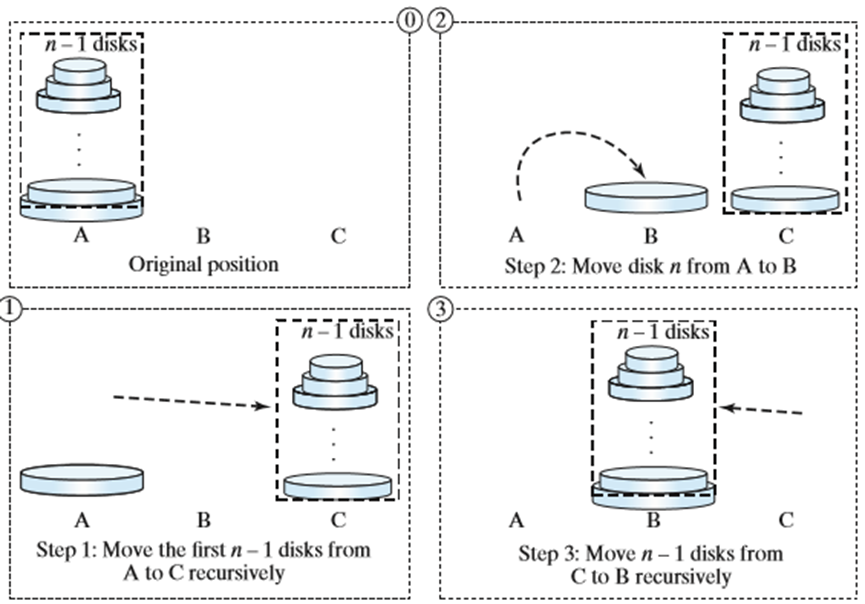
- n>1 时分解为三个子问题:
- 借助塔 B 将前 n-1 个盘子从 A 移到 C;
- 将盘子 n 从 A 移到 B;
- 借助塔 A 将 n-1 个盘子从 C 移到 B。
![image]()
完整代码
package com.recusive;
/**
* 汉诺塔
* @author Jing61
*/
public class Hanoi {
public static void main(String[] args) {
hanoi(3, 'A', 'B', 'C');
}
/**
* 汉诺塔
* @param n 盘子数量
* @param a 源柱
* @param b 目标柱
* @param c 临时柱
*/
public static void hanoi(int n, char a, char b, char c) {
if(n == 1) {
System.out.println("将盘子1从" + a + "柱移动到" + b + "柱");
}
else {
hanoi(n - 1, a, c, b);
System.out.println("将盘子" + n + "从" + a + "柱移动到" + b + "柱");
hanoi(n - 1, c, b, a);
}
}
}
递归与迭代
递归的缺点
- 系统开销大:调用方法时需为局部变量和参数分配空间,占用大量内存,且需额外时间管理内存;
- 可能存在效率问题:相比迭代,递归可能更耗时。
递归的优势
- 对于本质上具有递归特性的问题(如目录遍历、汉诺塔),递归能提供清晰、简单的解决方案,而迭代实现难度极大。
核心结论
任何递归问题都可通过迭代解决,但递归的价值在于简化复杂问题的编程实现,提升代码可读性。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号