GCD 与 LCM
GCD与LCM
本文将系统讲解两个核心概念——最大公约数(GCD) 和 最小公倍数(LCM),包括定义、性质、数学证明、编程实现及应用场景。
最大公约数(GCD)
GCD定义
整数a和b的最大公约数(Greatest Common Divisor,简称GCD),是指能同时整除a和b的所有正整数中最大的那个,记为gcd(a, b)。
- 示例:gcd(15, 81) = 3(3是能同时整除15和81的最大整数)。
- 注意:由于正负数的因子完全相同(如-15的因子与15一致),因此gcd(a, b) = gcd(|a|, |b|)。编程时只需处理正整数,简化逻辑。
GCD核心性质
GCD具有多个重要性质,是推导算法和解决问题的基础:
- 辗转性:gcd(a, b) = gcd(a, a + b) = gcd(a, k * a + b)(k为任意整数)。
- 例:gcd(5, 3) = gcd(5, 5 + 3) = gcd(5, 8) = 1。
- 数乘性:gcd(k * a, k * b) = k * gcd(a, b)(k为正整数)。
- 例:gcd(2 * 3, 2 * 5) = 2 * gcd(3, 5) = 2 * 1 = 2。
- 多变量扩展性:多个整数的 GCD 可通过两两计算推导,即gcd(a, b, c) = gcd[gcd(a, b), c]。
- 例:gcd(4, 6, 8) = gcd[gcd(4,6), 8] = gcd(2, 8) = 2。
- 互素性:若gcd(a, b) = d,则gcd(a / d, b / d) = 1(即a / d与b / d互素,没有除1外的公约数)。
- 例:gcd(12, 18) = 6,则gcd(12 / 6, 18 / 6) = gcd(2, 3) = 1。
- 消去性:gcd(a + c * b, b) = gcd(a, b)(c为任意整数)。
- 例:gcd(5 + 2 * 3, 3) = gcd(11, 3) = 1,与gcd(5, 3) = 1一致。
GCD编程实现:欧几里得算法
欧几里得算法(又称辗转相除法)是计算 GCD 的高效算法,核心公式为:
gcd(a, b) = gcd(b, a % b)()
- 边界条件:若b = 0,则gcd(a, 0) = a。
- 适用范围:a ≥ 0,b > 0,若b等于0,则结果为0(若 a < b,第一次递归会自动交换位置,如gcd(3, 5) = gcd(5, 3 % 5) = gcd(5, 3)。
证明
欧几里得算法的正确性可通过以下两步证明:
证明1:(a, b)与(b, a % b)的公约数完全相同
设a = k * b + r(其中r = a % b,满足0 ≤ r < b):
- 若d是a和b的公约数,则r = a - k * b可被d整除(因a和k * b均能被d整除),故d也是b和r的公约数。
- 若d是b和r的公约数,则a = k * b + r可被d整除(因k * b和r均能被d整除),故d也是a和b的公约数。
因此,(a, b)与(b, a % b)的公约数集合完全一致,最大公约数也必然相等。
证明2:基于素数分解的验证
设c = gcd(a, b),则可将a和b表示为:
a = m * c,b = n * c(其中m和n为互素的正整数,即gcd(m, n) = 1)。
由r = a % b可知r = a - q * b(q为商,正整数),代入a和b的表达式:
r = m * c - q * n * c = (m - q * n) * c
此时b = n * c,r = (m - q * n) * c,且n与(m - q * n)互素(反证法:若n与(m - q * n)有公约数 ,则n = x * d,m - q * n = y * d其中x,y,d都是正整数,且d > 1,则 a = m * c = (q * x + y) * d * c,b = x * d * c,这时a,b的最大公约数变成d * c,与前提矛盾,所以n,m - q * n一定互质)。
因此gcd(b, r) = c = gcd(a, b),即gcd(a, b) = gcd(b, a % b)。
代码实现
- java
/** * 欧几里得算法计算最大公约数(GCD) * @param a 整数a(非负) * @param b 整数b(非负,且不与a同时为0) * @return a和b的最大公约数 */ int gcd(int a, int b) { // 边界条件:若b为0,返回a(a此时非负) if (b == 0) { return a; } // 递归调用:gcd(a,b) = gcd(b, a%b) return gcd(b, a % b); } - C++
int gcd(int a, int b) { if (b == 0) { return a; } return gcd(b, a % b); }
最小公倍数(LCM)
LCM定义
整数a和b的最小公倍数(Least Common Multiple,简称LCM),是指能同时被a和b整除的所有正整数中最小的那个,记为lcm(a, b)。
- 示例:lcm(5, 6) = 30(30是能同时整除5和6的最小整数)。
- 注意:若a或b为0,LCM 无意义,编程时需确保输入为非零整数。
LCM与GCD的关系:基于算数基本定理
算数基本定理
任何大于1的正整数n,都可唯一分解为有限个素数的乘积(素数因子从小到大排列):
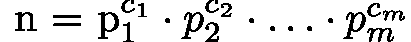
其中p_i为素数且从小到大,C_i为正整数(素数的指数)。
GCD与LCM的素数分解表达式
设整数a和b的素数分解为:
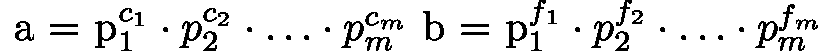
(若某素数仅在一个数中出现,另一数的对应指数取0,如a = 2 ^ 3,b = 3 ^ 2,则a = (2 ^ 3) * (3 ^ 0)),b = (2 ^ 0) * (3 ^ 2))。
则:
- GCD取各素数的最小指数:
![latex-1762221053733]()
- LCM取各素数的最大指数:
![latex-1762221062772]()
核心公式:lcm(a, b) = (a * b) / gcd(a, b)
由素数分解表达式可推导:
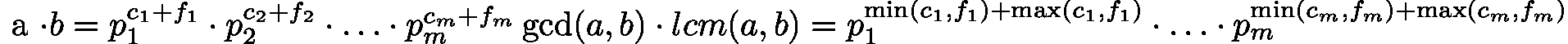
由于min(x, y) + max(x, y) = x + y,因此:
gcd(a, b) * lcm(a, b) = a * b
整理得 LCM 计算公式:
lcm(a, b) = (a * b) / gcd(a, b)
关键优化:计算时需先做除法再做乘法(即a / gcd(a, b) * b ),避免a * b超出整数范围导致溢出(如a = 10 ^ 9,b = 10 ^ 9,a * b = 10 ^ 18,超出int范围,但 a / gcd(a, b) * b = 1 * 10 ^ 9 = 10 ^ 9无溢出)。
LCM编程实现
基于GCD函数,直接套用核心公式即可实现LCM,需注意处理输入不为0的情况。
代码实现
- java
/** * 计算最小公倍数(LCM):基于GCD公式 * @param a 正整数a * @param b 正整数b * @return a和b的最小公倍数 */ int lcm(int a, int b) { // 处理输入为0的情况 if (a == 0 || b == 0) { return -1; } return a / gcd(a, b) * b; } // 复用之前实现的GCD函数 int gcd(int a, int b) { if (b == 0) { return a; } return gcd(b, a % b); } - C++
int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); } int lcm(int a, int b) { return (a == 0 || b == 0) ? -1 : a / gcd(a, b) * b; }
总结
| 概念 | 核心公式/定理 | 编程实现核心 | 典型应用场景 |
|---|---|---|---|
| GCD | gcd(a, b) = gcd(b, a % b) | 欧几里得算法(递归/迭代) | 约分、LCM计算、裴蜀定理前置 |
| LCM | lcm(a, b) = (a * b) / gcd(a,b) | 基于GCD推导 | 分数通分、周期计算(如两个事件同时发生的时间) |


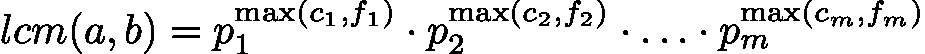

 浙公网安备 33010602011771号
浙公网安备 33010602011771号