二分法
理论背景
在科学计算和算法竞赛中,求解单变量非线性方程 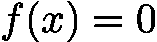 (其中
(其中 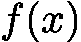 为连续函数)是常见问题。本文将详细介绍两种核心解法——搜索法和二分法,并重点拆解二分法在整数和实数场景下的应用、模板代码及实战技巧。
为连续函数)是常见问题。本文将详细介绍两种核心解法——搜索法和二分法,并重点拆解二分法在整数和实数场景下的应用、模板代码及实战技巧。
对于单变量非线性方程 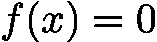 ,我们的目标是找到使得函数值为 0 的根
,我们的目标是找到使得函数值为 0 的根 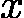 。以下两种方法均基于“区间搜索”思想,通过逐步缩小根的可能范围,最终得到满足精度要求的近似解。
。以下两种方法均基于“区间搜索”思想,通过逐步缩小根的可能范围,最终得到满足精度要求的近似解。
搜索法
搜索法是最直观的区间查找方法,核心是通过“等分区间+符号判断”定位根的位置。
基本原理
- 确定初始区间:选择区间
![latex-1761817935925]() ,满足
,满足 ![latex-1761817950255]() (即区间两端函数值异号,根据介值定理,区间内至少存在一个实根)。
(即区间两端函数值异号,根据介值定理,区间内至少存在一个实根)。 - 等分区间:将
![latex-1761817935925]() 分成 n 个等分的子区间,每个子区间长度为
分成 n 个等分的子区间,每个子区间长度为 ![latex-1761817976470]() 。
。 - 计算函数值:对每个分点
![latex-1761817998949]() ,计算
,计算 ![latex-1761818011400]() :
:
- 若
![latex-1761818038690]() ,则
,则 ![latex-1761818056265]() 是方程的一个实根。
是方程的一个实根。 - 若
![latex-1761818067642]() ,则根在子区间
,则根在子区间 ![latex-1761818082872]() 内,可近似取区间中点
内,可近似取区间中点 ![latex-1761818097708]() 作为根的近似值。
作为根的近似值。
- 若
特点
- 优点:逻辑简单,易于实现,可定位多个根(若区间内存在多个根,可通过多个子区间的符号变化发现)。
- 缺点:精度依赖于区间等分数量 n,n 越大精度越高,但计算量也随之增加,效率较低。
二分法
二分法(Bisection Method)是在搜索法基础上优化的“逐步缩窄区间”方法,通过反复将区间二等分,快速定位根的位置,效率远高于普通搜索法。
基本原理
- 确定初始区间:同搜索法,选择
![latex-1761818132341]() 满足
满足 ![latex-1761818152891]() 。
。 - 计算区间中点:计算中点
![latex-1761818163747]() 。
。 - 判断中点与根的关系:
- 若
![latex-1761818178283]() :
:![latex-1761818202033]() 即为根,直接返回。
即为根,直接返回。 - 若
![latex-1761818259900]() :根在左区间
:根在左区间 ![latex-1761818270824]() ,更新右边界
,更新右边界 ![latex-1761818282857]() 。
。 - 若
![latex-1761818300597]() :根在右区间
:根在右区间 ![latex-1761818310561]() ,更新左边界
,更新左边界 ![latex-1761818321183]() 。
。
- 若
- 重复迭代:重复步骤 2~3,直到区间长度
![latex-1761818335359]() (
(![latex-1761818387841]() 为预设精度阈值),此时区间内任意点(通常取中点)均可作为近似根。
为预设精度阈值),此时区间内任意点(通常取中点)均可作为近似根。
适用条件与局限性
- 适用条件:
- 函数
![latex-1761817862180]() 在区间
在区间 ![latex-1761818437249]() 上连续。
上连续。 - 区间两端函数值异号(
![latex-1761818473149]() )。
)。
- 函数
- 局限性:
- 无法处理“重根”(如
![latex-1761818506472]() ,虽有根但区间两端符号相同)。
,虽有根但区间两端符号相同)。 - 若区间内存在多个根,仅能找到其中一个(取决于初始区间和迭代过程)。
- 不适用于非单调函数的“孤立根”定位(需结合其他方法)。
- 无法处理“重根”(如
核心分类
根据求解场景的不同,二分法可分为 整数二分 和 实数二分,两者在取整规则、迭代终止条件上存在差异。
整数二分
整数二分针对“有序整数序列”的查找场景,核心是通过“左中位数”或“右中位数”的选择,避免迭代过程中出现死循环,常见需求包括“找 x 或 x 的后继”“找 x 或 x 的前驱”。
关键概念:中位数选择
- 左中位数:向下取整,
![latex-1761818564384]() (或
(或 ![latex-1761818573443]() ),更靠近左边界。
),更靠近左边界。 - 右中位数:向上取整,
![latex-1761818599105]() (或
(或 ![latex-1761818610125]() ),更靠近右边界。
),更靠近右边界。
中位数的选择需与“区间更新规则”匹配,否则会导致死循环(如左边界更新为 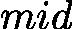 时,若用左中位数可能永远无法缩小区间)。
时,若用左中位数可能永远无法缩小区间)。
场景1:在单调递增序列中找 x 或 x 的后继
定义
在单调递增序列 a[] 中:
- 若存在 x,找到第一个等于 x 的位置。
- 若不存在 x,找到第一个大于 x 的位置(即 x 的后继)。
示例
序列 a[] = {-12, -6, -4, 3, 5, 5, 8, 9}(长度 n=8 ),索引 0~7:
- 查找 x=-5:无 -5,返回第一个大于 -5 的位置 2(对应 a[2]=-4)。
- 查找 x=7:无 7,返回第一个大于 7 的位置 6(对应 a[6]=8)。
- 查找 x=12:大于最大元素 9,返回位置 8(越界,需在代码中特殊处理)。
模板代码(左闭右开区间 [0, n))
#include<bits/stdc++.h>
using namespace std;
#define ll long long
// a[]: 单调递增序列,n: 序列长度,x: 目标值
// 返回:x的后继位置(或第一个x的位置)
int bin_search(int a[], int n, int x) {
int left = 0, right = n; // 左闭右开区间 [0, n)
while (left < right) { // 区间长度大于0时循环
int mid = (left + right) >> 1; // 左中位数(向下取整)
if (a[mid] >= x) { // 若mid位置元素>=x,说明目标在左区间
right = mid;
} else { // 若mid位置元素<x,说明目标在右区间
left = mid + 1;
}
}
return left; // 循环结束后 left == right,即为目标位置
}
int main() {
ios::sync_with_stdio(false); // 加速输入输出
cin.tie(0);
cout.tie(0);
int n;
int a[100];
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
int x;
cin >> x;
cout << bin_search(a, n, x) << endl;
return 0;
}
关键逻辑解释
- 区间更新规则:当
![latex-1761818740204]() 时,目标可能在
时,目标可能在 ![latex-1761818748333]() (包括 mid),故更新
(包括 mid),故更新 ![latex-1761818760834]() ;当
;当 ![latex-1761818769488]() 时,目标必在
时,目标必在![latex-1761818777236]() ,故更新
,故更新 ![latex-1761818785245]() 。
。 - 避免死循环:若将
![latex-1761818795143]() 改为
改为 ![latex-1761818803075]() ,当
,当 ![latex-1761818810404]() 时,
时,![latex-1761818818178]() ,区间始终为 [2,3],陷入死循环。
,区间始终为 [2,3],陷入死循环。
场景2:在单调递增序列中找 x 或 x 的前驱
定义
在单调递增序列 a[] 中:
- 若存在 x,找到最后一个等于 x 的位置。
- 若不存在 x,找到最后一个小于 x 的位置(即 x 的前驱)。
模板代码(左闭右开区间 [0, n))
#include<bits/stdc++.h>
using namespace std;
#define ll long long
// a[]: 单调递增序列,n: 序列长度,x: 目标值
// 返回:x的前驱位置(或最后一个x的位置)
int bin_search(int a[], int n, int x) {
int left = 0, right = n; // 左闭右开区间 [0, n)
while (left < right) { // 区间长度大于0时循环
int mid = (left + right + 1) >> 1; // 右中位数(向上取整)
if (a[mid] <= x) { // 若mid位置元素<=x,说明目标在右区间
left = mid;
} else { // 若mid位置元素>x,说明目标在左区间
right = mid - 1;
}
}
return left; // 循环结束后 left == right,即为目标位置
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
int a[100];
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
int x;
cin >> x;
cout << bin_search(a, n, x) << endl;
return 0;
}
关键逻辑解释
- 右中位数选择:若用左中位数
![latex-1761818869106]() ,当
,当 ![latex-1761818876012]() 时,
时,![latex-1761818885242]() ,若
,若 ![latex-1761818892327]() ,更新
,更新 ![latex-1761818902359]() ,区间始终为 [2,3],陷入死循环;右中位数可避免此问题。
,区间始终为 [2,3],陷入死循环;右中位数可避免此问题。 - 区间更新规则:当
![latex-1761818910907]() 时,目标可能在
时,目标可能在 ![latex-1761818920529]() (包括 mid),故更新
(包括 mid),故更新 ![latex-1761818928949]() ;当
;当 ![latex-1761818936665]() 时,目标必在
时,目标必在 ![latex-1761818945523]() ,故更新
,故更新 ![latex-1761818954216]() 。
。
工具函数:lower_bound 与 upper_bound
C++ 标准库 <algorithm> 提供了两个整数二分工具函数,需先对序列排序(sort(a, a+n)),本质是对“后继/前驱”场景的封装。
| 函数 | 功能描述 | 返回值 |
|---|---|---|
lower_bound(a, a+n, x) |
找第一个大于等于 x 的元素 | 该元素的地址 |
upper_bound(a, a+n, x) |
找第一个大于 x 的元素 | 该元素的地址 |
地址转位置
通过“地址差”计算元素在数组中的索引: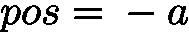 。
。
常见用法示例
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
int a[100];
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
sort(a, a + n); // 必须先排序!
int x;
cin >> x;
// 1. 找x或x的后继(第一个>=x的位置)
int pos1 = lower_bound(a, a + n, x) - a;
// 2. 找第一个>x的位置
int pos2 = upper_bound(a, a + n, x) - a;
// 3. 找x或x的前驱(最后一个<=x的位置)
int pos3 = upper_bound(a, a + n, x) - a - 1;
// 4. 找最后一个<x的位置
int pos4 = lower_bound(a, a + n, x) - a - 1;
cout << pos1 << endl;
cout << pos2 << endl;
cout << pos3 << endl;
cout << pos4 << endl;
return 0;
}
输入输出示例
输入1:
5
1 3 5 7 9
5
输出1:
2 // pos1:第一个>=5的位置(a[2]=5)
3 // pos2:第一个>5的位置(a[3]=7)
2 // pos3:最后一个<=5的位置(a[2]=5)
1 // pos4:最后一个<5的位置(a[1]=3)
输入2:
5
1 3 5 7 9
2
输出2:
1 // pos1:第一个>=2的位置(a[1]=3)
1 // pos2:第一个>2的位置(a[1]=3)
0 // pos3:最后一个<=2的位置(a[0]=1)
0 // pos4:最后一个<2的位置(a[0]=1)
整数二分建模思路
对于复杂问题(如“最大值最小化”“最小值最大化”),可通过“二分答案+check函数”建模,核心步骤如下:
- 确定答案范围:定义左边界
left和右边界right(答案的可能取值范围)。 - 设计 check 函数:判断当前中点
mid是否为“合法答案”(或是否满足目标条件)。 - 迭代缩窄区间:根据
check(mid)的结果更新left或right,记录合法答案。
模板框架
while (left < right) {
int ans; // 存储合法答案
int mid = (left + right) / 2; // 或右中位数,根据场景选择
if (check(mid)) { // mid是合法答案,尝试找更优解
ans = mid;
// 若找“最大值最小化”,更新右边界(缩小答案范围)
right = mid;
// 若找“最小值最大化”,更新左边界(扩大答案范围)
// left = mid;
} else { // mid不合法,调整区间
// 不合法则向相反方向更新
left = mid + 1; // 或 right = mid - 1
}
}
return left; // 最终答案
实数二分
实数二分针对“连续函数求根”场景,无需考虑整数取整问题,迭代终止条件基于“区间长度是否小于精度阈值”,逻辑更简洁。
基本模板
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const double eps = 1e-7; // 精度阈值(根据需求调整,如1e-6、1e-8)
// check函数:判断mid是否满足目标条件(需根据具体问题实现)
bool check(double mid) {
// 示例逻辑(需替换为实际问题的条件)
// ...
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
// 1. 确定初始区间 [left, right](需满足f(left)*f(right) < 0)
double left = ...;
double right = ...;
// 2. 迭代缩窄区间,直到满足精度
while (right - left > eps) { // 区间长度小于eps时终止
double mid = (left + right) / 2; // 实数中点(无需取整)
if (check(mid)) { // mid满足条件,根在左区间
right = mid;
} else { // mid不满足条件,根在右区间
left = mid;
}
}
// 3. 输出近似根(left或right均可,误差小于eps)
printf("%.6f\n", left); // 按需求控制输出小数位数
return 0;
}
精度调整技巧
- 超时问题:若迭代次数过多导致超时,可增大
eps(如从 1e-8 调整为 1e-6),减少迭代次数。 - 精度不足问题:若答案误差过大,可减小
eps(如从 1e-6 调整为 1e-8 ),但需注意迭代次数增加可能导致超时。
实战例题
题目背景(简化)
已知路程 s ,甲速度 a ,乙速度 b(a < b)。甲从起点出发,乙从终点出发,中途乙可能等待甲。求两人相遇的最短时间。
代码实现
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const double eps = 1e-7;
double s, a, b; // s:总路程,a:甲速度,b:乙速度
// check函数:判断乙等待mid时间后,是否能让相遇时间更短
bool check(double mid) {
bool f = false;
double t1 = mid / b; // 乙先出发t1时间(走了mid距离)
double t2 = (mid - t1 * a) / (a + b); // 两人相向而行的时间
// 比较两种方案的时间:乙等待后相遇时间 vs 乙不等待相遇时间
if (t1 + (s - mid) / a >= t1 + t2 + (s - (t1 + t2) * a) / b) {
f = true;
}
return f;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> s >> a >> b;
double left = 0, right = s; // 初始区间:乙最多走完全程s
while (left - right > eps) { // 迭代缩窄区间
double mid = left + (right - left) / 2; // 等价于(左+右)/2,避免溢出
if (check(mid)) {
right = mid;
} else {
left = mid;
}
}
// 计算最短相遇时间并输出(保留6位小数)
printf("%.6f", left / b + (s - left) / a);
return 0;
}
注意事项
- 避免溢出:计算中点时,若
left + right可能超过数据类型范围(如 int 最大值 2e9),建议用mid = left + (right - left) / 2替代mid = (left + right) / 2,两者等价但可避免溢出。 - 区间定义一致性:整数二分中,区间定义(如左闭右开 [0,n)、闭区间 [0,n-1])需与更新规则匹配,否则易出错。
- sort 前置:使用
lower_bound和upper_bound前,必须先对数组排序,否则函数行为未定义。 - check 函数正确性:二分建模的核心是
check函数,需确保其逻辑能准确判断“中点是否合法”,否则会导致答案错误。


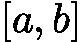 ,满足
,满足 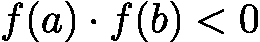 (即区间两端函数值异号,根据介值定理,区间内至少存在一个实根)。
(即区间两端函数值异号,根据介值定理,区间内至少存在一个实根)。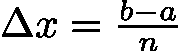 。
。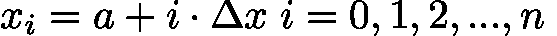 ,计算
,计算 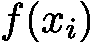 :
:
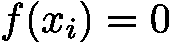 ,则
,则 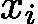 是方程的一个实根。
是方程的一个实根。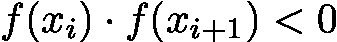 ,则根在子区间
,则根在子区间 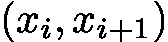 内,可近似取区间中点
内,可近似取区间中点 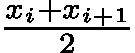 作为根的近似值。
作为根的近似值。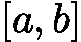 满足
满足 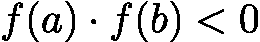 。
。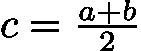 。
。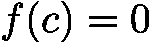 :
: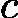 即为根,直接返回。
即为根,直接返回。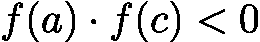 :根在左区间
:根在左区间 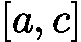 ,更新右边界
,更新右边界 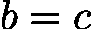 。
。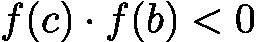 :根在右区间
:根在右区间 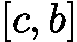 ,更新左边界
,更新左边界 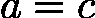 。
。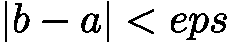 (
(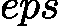 为预设精度阈值),此时区间内任意点(通常取中点)均可作为近似根。
为预设精度阈值),此时区间内任意点(通常取中点)均可作为近似根。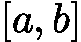 上连续。
上连续。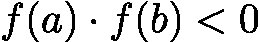 )。
)。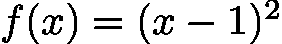 ,虽有根但区间两端符号相同)。
,虽有根但区间两端符号相同)。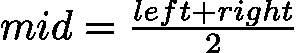 (或
(或 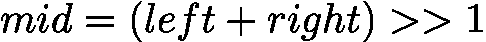 ),更靠近左边界。
),更靠近左边界。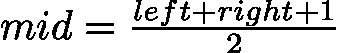 (或
(或 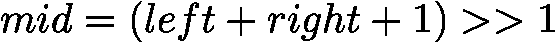 ),更靠近右边界。
),更靠近右边界。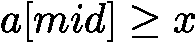 时,目标可能在
时,目标可能在 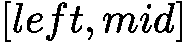 (包括 mid),故更新
(包括 mid),故更新 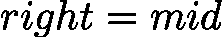 ;当
;当 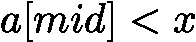 时,目标必在
时,目标必在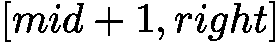 ,故更新
,故更新 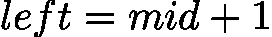 。
。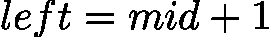 改为
改为 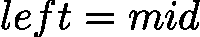 ,当
,当 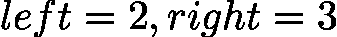 时,
时,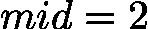 ,区间始终为 [2,3],陷入死循环。
,区间始终为 [2,3],陷入死循环。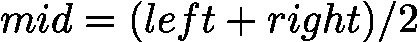 ,当
,当 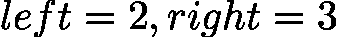 时,
时,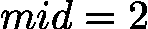 ,若
,若 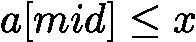 ,更新
,更新 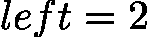 ,区间始终为 [2,3],陷入死循环;右中位数可避免此问题。
,区间始终为 [2,3],陷入死循环;右中位数可避免此问题。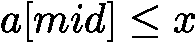 时,目标可能在
时,目标可能在 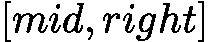 (包括 mid),故更新
(包括 mid),故更新 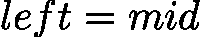 ;当
;当 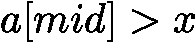 时,目标必在
时,目标必在 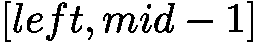 ,故更新
,故更新 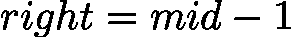 。
。
 浙公网安备 33010602011771号
浙公网安备 33010602011771号