索引详解

一.什么是索引？

　　1.索引

　　　一种帮助数据库高效获取（已经排序而且查找快）数据的数据结构，记住，它是一种数据结构。那么根据已经学习了的数据结构，它是用的哪种呢？别急，先来了解一下索引的分类。

　　2.索引的分类

　　　1.B-Tree索引：大部分引擎支持，这也是我们学习的重点，也是平时使用最多的。

　　　2.Full_text（全文索引）：MyISAM引擎支持，作用在CHAR、VARCHAR ，TEXT 列上，为了解决WHERE name LIKE “%word%"这类针对文本的模糊查询效率较低的问题。

　　　3.HASH索引：Memory引擎支持，用得较少，不做详细讨论。

　　3.聚合索引与非聚合索引2018-11-05聚合索引：从底层实现上来说，也就是采用B+Tree结构，叶子节点存放着整行的数据，其他节点没有数据，只是存放键值和指向数据页的偏移量，通俗地说就是存放指向数据页的路标，告诉你去哪里找数据页。聚合索引的数据已经排好序，比如说英文字典里面字母a的单词都在一个连续的区域，正文已经排好序，就是聚合索引。

　　　非聚合索引：和聚合索引相反，叶子节点存的只是最终数据的指引，并不包含行数据，通过找到这个指引，再去找行数据。比如说查新华字典，你想查你这个字，你先找偏旁，找到你个字的页数就是找到这个指引，再根据这个指引（页码）去找你这个字（最终的行数据）。

 

二.索引的使用

　　1.适用场景与不适用场景

　　　　<1>.频繁作为查询条件的字段也应该建立索引,比如一个用户表，id和name是经常用于查询的，主键已经建立唯一索引，所以很有必要将name也建立一个索引。

　　　　<2>与其他表关联，外键关系也要建立索引。

　　　　<3>频繁更新增删改的字段不适合建立索引，因为建立索引修改索引也是耗费时间和资源的。

　　　　<4>列中重复数而且平均分配太多,比如性别列，只有男女，建个锤子索引喔。

　　2.使用方法

　　　　<1>建立索引：普通创建create INDEX +索引名字+ on +table名字+（列名1，列名2），

　　　　　　　　　　   修改表时ALTER TABLE 表名 ADD INDEX 索引名 （列名1）

　　　　　　　　　　   建表时创建create table （[ UNIQUE | FULLTEXT | SPATIAL ]  INDEX | KEY [ 别名]  

　　　　<2>索引失效情况：

　　　　　a.最佳左前缀原则：最佳左前缀意思是，查询要按照索引列的顺序，最左边那个必须要有，例子中就是a啦，可以把它理解成火车头，没有它车是开不了的。如果是组合索引（a，b，c）,当你用where查询的时候，比如说where a =1，b =2，c=3，这样是可以的（全值匹配，又称覆盖索引），然后就是如果中间有范围查询，比如where a= 1，b>2,那么a，b这两个索引还是有用到的，后面的c就失效了。最后，不能跳过其中一项，查询a，c没有b也是不行的。

　　　　　b.索引列不要秀操作：什么计算啊，用函数啊，varchar没有加单引号引起自动类型转换啊，都会引起索引失效的。

　　　　　c.范围条件后面的失效，前面有说啦。

　　　　　d.尽量使用覆盖索引，就是说查询的尽量和索引对应，不全部对应部分对应也行啊。

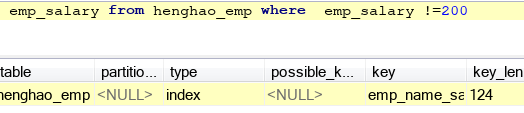
　　　　　e.不要用！=和<>，记住吧。

　　　　　f.is null和is not null，or少用，不是不用喔，少。

　　　　　g.当查询的是*时，用like模糊查询，%在前面会引起索引失效，放在后面吧...

　　　<3>实践：

　　　　a.我创建的索引是（emp_name,emp_salary）,当select的字段为组合索引里面的字段（不用按顺序都可以）时，后面的where查询不用符合最左都可以，如下图：

　　　　

　　　　而当你select的字段不是索引里面的字段，如*或者其他字段，就不会使用到索引，如下面这个，emp_deptid不是索引列，所以就算where那里符合最左前缀也没用啊，当然了*更加不用说了。

 

                                                                                              

　　　　b.关于like模糊查询，有点迷，在测试时发现，就算前后都有%，当select的字段为索引列里面的（不一定按顺序），都用到了索引，不是说好了索引失效？

下图里面，不仅是where那里没有最佳左前缀（没有emp_name），还使用了前后%，但是select那里用到了索引列的字段，一样使用到组合索引啊，还有更加神奇的在后面，搞得我真的十分迷，希望有高手能帮帮小弟解答迷惑。

                                        

　　　　c.关于不要在索引列做计算，不要用！=,<>，范围查询等，看看例子，第一张是索引列做计算的，第二张是范围的，第三张是不等，神奇地，都用了索引，以上测试如果select的字段不是索引列时就失效，说明，这些索引失效是指select的字段不为索引的字段时产生的，以后查询尽量使用索引列。

　　　　                                    

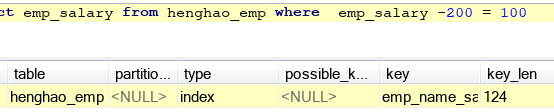
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　范围查询

　　　　　　　　　　　     　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　不等

　　　　　                              　

 

                                  

三.索引的原理----B+Tree详解

　　1.what is B+Tree?

　　　a.定义：B，意思是Balance，平衡，对的，它是一种极端平衡的多路查找树，是为了磁盘或者其他直接存取设备设计的平衡查找树，不是二叉喔，是一种平衡的多路查找树，（平衡多路查找树已经提到三四次了，看到这应该对这个定义蛮深刻了吧哈哈哈）。它有个兄弟，或者说大哥吧，BTree，具体区别后面再说，下面说下它的性质。

　　　b.性质：我们先来看看一个图，对的，B+树的图解：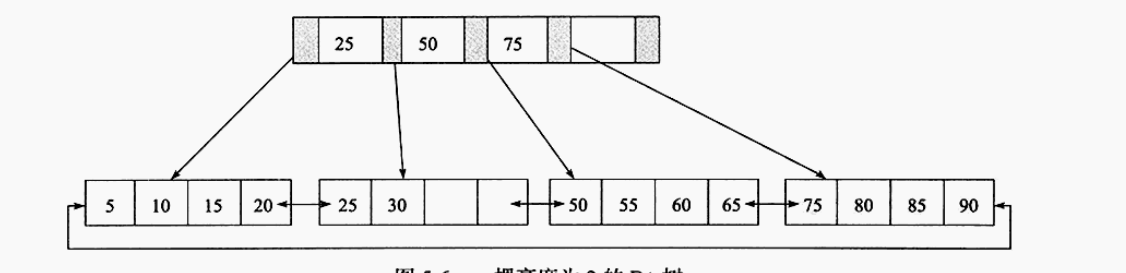

　　　　

　　c.下面我们详细解读一下它：

　　　　1.阶数m，就是分支数，一般一个m阶的B+Tree，根节点的分支>=2,其他节点的在[m/2,m]这个区间，又可以叫它做：m/2（向上取整，忽略小数整数加一，5/3是2）-m树。

　　　　2.关键码n，图中根节点中数字之间的那个阴影部分，n一般在[m/2,m-1]这个区间，它是指向子节点的指针。

　　d.举例：查找数据30过程如下：

　　　　1.根节点是加载到内存来遍历的，遍历根节点的数据，找到适合的指针（图中第二个关键码）

　　　　2.根据这个关键码，到磁盘中（磁盘IO耗费时间最多，不过B+树的好处就在这，大大减少了磁盘IO的次数，想想如果是BST该IO多少次）寻找子节点，加载到内存。

　　　　3.继续遍历这个子节点，发现第二个就找到了，很快，很舒服，nice。