软工第三次作业——结对项目
学号:3123004657 姓名:黄健峰
学号:3123004660 姓名:黄梓聪
1. 效能分析
改进:
(1) 将项目的四则运算式存储方式改为表达式树数组
原存储方式:将所有四则运算式分为两个二维数组,一个数组存储式子中的符号和括号,一个数组存储式子中参与运算的数
修改原因:原存储方式容易容易出现不止一种排列顺序的情况,且验证是否合规所需时间较长
(2) 增加尝试生成运算符号和当前条件下生成符合要求的运算式的次数上限
修改后:当超过预设的次数上限时,会降低要生成的运算式的复杂度(如减少运算符个数,限制括号等)
修改原因:防止生成时间过长
2. 设计实现过程
Myapp.cpp
依赖 FileMana.hpp、CounterGenerator.hpp、AnswerCheck.hpp
负责解析命令行、调度“生成题目/校验答案”、文件读写
CounterGenerator.hpp
依赖 Fraction.hpp
负责按约束随机生成表达式树、去重、输出题目与答案
AnswerCheck.hpp
依赖 Fraction.hpp
负责读取 Exercises.txt/Answers.txt 文本、解析与对比答案
FileMana.hpp
独立文件 I/O 封装,被 Myapp 调用
Fraction.hpp
基础数值类型,提供分数构造、化简与四则运算,供 CounterGenerator 与 AnswerCheck 使用
设计时:根据题目要求分为:FileMana,AnswerCheck,CounterGeneration三个类,在实现过程中,发现AnswerCheck和CounterGeneration对分数的存储和存在形式有共同的需求,因此独立出来一个类Fraction,又因仅CounterGeneration需要对运算式进行特殊存储,因此在CounterGeneration内实现内部类ExprNode;
函数build_random_expr流程图
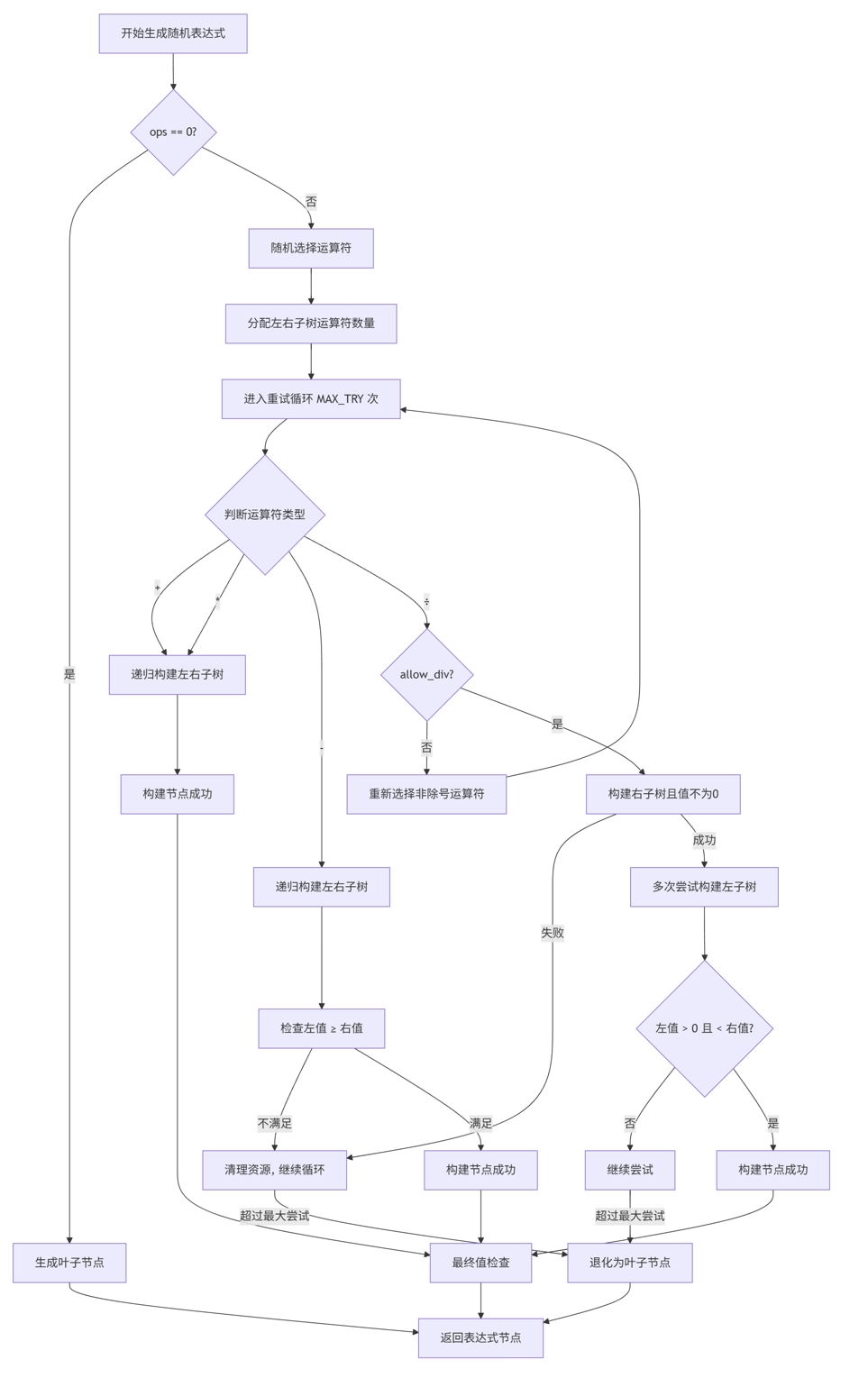
函数generate_counters流程图

函数checkAnswer流程图

3. 代码说明
/**
* @brief 生成随机表达式树
* @param ops 运算符数量,决定表达式的复杂度
* @param allow_div 是否允许除法运算
* @return 表达式树根节点指针
*/
ExprNode* build_random_expr(int ops, bool allow_div) {
// 基线情况:没有运算符时生成叶子节点(操作数)
if (ops == 0) {
return make_leaf();
}
// 随机选择运算符,考虑是否允许除法
std::string op = random_operator(allow_div);
// 分配运算符给左右子树:总运算符数 = 当前运算符 + 左子树运算符 + 右子树运算符
int left_ops = (ops == 1) ? 0 : random_int(0, ops - 1);
int right_ops = (ops - 1) - left_ops;
// 重试机制:防止因约束条件反复失败
const int MAX_TRY = 200;
for (int t = 0; t < MAX_TRY; ++t) {
// 创建当前运算符节点
ExprNode* node = new ExprNode(op, true);
ExprNode* L = nullptr;
ExprNode* R = nullptr;
// 根据不同运算符类型处理子树构建
if (op == "+" || op == "*") {
// 加法和乘法:直接递归构建左右子树,无特殊约束
L = build_random_expr(left_ops, allow_div);
R = build_random_expr(right_ops, allow_div);
} else if (op == "-") {
// 减法:确保左子树值 ≥ 右子树值,避免负数结果
L = build_random_expr(left_ops, allow_div);
R = build_random_expr(right_ops, allow_div);
Fraction lv = L->calculate();
Fraction rv = R->calculate();
// 检查约束条件,不满足则清理资源并重试
if (!frac_ge(lv, rv)) {
delete_tree(L);
delete_tree(R);
delete node;
continue; // 继续重试循环
}
} else { // 除法运算 "÷"
// 检查是否允许除法,不允许则重新选择运算符
if (!allow_div) {
delete node;
op = random_operator(false);
continue;
}
// 构建右子树并确保其值不为0
R = make_positive_subtree(right_ops, allow_div);
Fraction rv = R->calculate();
if (frac_is_zero(rv)) {
delete_tree(R);
delete node;
continue;
}
// 构建左子树:需要满足 0 < 左子树值 < 右子树值(真分数条件)
bool ok = false;
for (int tt = 0; tt < MAX_TRY; ++tt) {
if (L) {
delete_tree(L);
L = nullptr;
}
L = make_positive_subtree(left_ops, allow_div);
Fraction lv = L->calculate();
// 检查是否满足真分数条件
if (frac_less(lv, rv) && frac_gt_zero(lv)) {
ok = true;
break;
}
}
// 如果无法找到满足条件的左子树,清理资源并重试
if (!ok) {
delete_tree(L);
delete_tree(R);
delete node;
continue;
}
}
// 连接子树到当前节点
node->left = L;
node->right = R;
// 最终验证:再次检查运算约束条件(因为递归构建可能有变化)
if (op == "-") {
Fraction lv = L->calculate();
Fraction rv = R->calculate();
if (!frac_ge(lv, rv)) {
delete_tree(node); // 删除整个子树
continue;
}
} else if (op == "÷") {
Fraction lv = L->calculate();
Fraction rv = R->calculate();
if (!frac_gt_zero(rv) || !frac_gt_zero(lv) || !frac_less(lv, rv)) {
delete_tree(node);
continue;
}
}
// 所有约束条件满足,返回构建的表达式树
return node;
}
// 重试机制失败后的退化处理:生成简单叶子节点
// 避免因过于严格的约束条件导致无法生成表达式
return make_leaf();
}
设计思路:
- 递归构建:根据运算符数量递归构建左右子树
- 约束保证:确保减法结果非负,除法结果为真分数
- 重试机制:对可能失败的运算类型设置重试次数限制
- 退化处理:多次失败后生成简单叶子节点作为保底
/**
* @brief 生成题目
*/
void generate_counters() {
// 清理历史数据,准备新一轮生成
for (auto* p : expr_trees) delete_tree(p);
expr_trees.clear();
answers.clear();
// 使用集合记录已生成的表达式模式,用于去重
std::set<std::string> seen;
// 根据数值范围决定是否允许除法(当range小于2时,无法生成有效除法)
bool allow_div = (range > 2);
// 设置全局最大尝试次数,防止无限循环
const int MAX_GLOBAL_TRY = std::max(count * 50, 200);
int attempts = 0;
// 主生成循环:尝试生成复杂表达式(1-3个运算符)
while ((int)expr_trees.size() < count && attempts < MAX_GLOBAL_TRY) {
attempts++;
// 随机选择运算符数量(1-3个)
int ops = random_int(1, 3);
ExprNode* root = build_random_expr(ops, allow_div);
/**
* 深度验证函数:递归检查整个表达式树的合法性
* 特别是确保所有层级的减法和除法都满足约束条件
* build_random_expr 只保证顶层运算合法,但子表达式可能存在问题
*/
std::function<bool(ExprNode*)> validate = [&](ExprNode* n)->bool{
if (!n || !n->isOperator) return true; // 叶子节点总是合法的
// 递归验证左右子树
bool okL = validate(n->left);
bool okR = validate(n->right);
if (!okL || !okR) return false;
// 检查当前节点的运算约束
if (n->value == "-") {
Fraction lv = n->left->calculate();
Fraction rv = n->right->calculate();
if (!frac_ge(lv, rv)) return false; // 减法:左值 ≥ 右值
} else if (n->value == "÷") {
Fraction lv = n->left->calculate();
Fraction rv = n->right->calculate();
// 除法:分母不为0,分子分母都为正,且为真分数
if (!frac_gt_zero(rv) || !frac_gt_zero(lv) || !frac_less(lv, rv))
return false;
}
return true;
};
// 如果验证失败,清理并重试
if (!validate(root)) {
delete_tree(root);
continue;
}
/**
* 去重检查:通过规范化表达式检测等价表达式
* 规范化包括:排序交换律运算、统一格式等
* 例如: "1+2" 和 "2+1" 会被识别为重复
*/
ExprNode* norm = clone_tree(root);
norm = norm->normalize(); // 规范化表达式树
std::string key = norm->to_string(); // 生成规范化字符串作为唯一标识
delete_tree(norm);
// 检查是否已生成过等价表达式
if (seen.find(key) != seen.end()) {
delete_tree(root);
continue;
}
// 保存新的唯一表达式
seen.insert(key);
expr_trees.push_back(root);
}
/**
* 补充生成阶段:如果复杂表达式生成不足,改用简单表达式
* 使用1个运算符的表达式更容易生成且更容易满足约束条件
*/
while ((int)expr_trees.size() < count) {
int ops = 1; // 只使用1个运算符,降低复杂度
ExprNode* root = build_random_expr(ops, allow_div);
// 同样的去重检查流程
ExprNode* norm = clone_tree(root);
norm = norm->normalize();
std::string key = norm->to_string();
delete_tree(norm);
if (seen.insert(key).second) {
expr_trees.push_back(root);
} else {
delete_tree(root);
}
// 安全阀:如果尝试过多仍无法生成足够题目,提前退出
// 避免因过于严格的约束条件导致无限循环
if ((int)seen.size() > count * 5) break;
}
}
设计思路:
- 去重机制:通过规范化表达式和字符串比较避免重复题目
- 合法性验证:确保所有减法、除法运算满足数学约束
- 渐进策略:先尝试复杂表达式,失败后降级为简单表达式
- 资源管理:妥善处理内存,避免泄漏
4. 测试运行
前五次测试输入的参数:
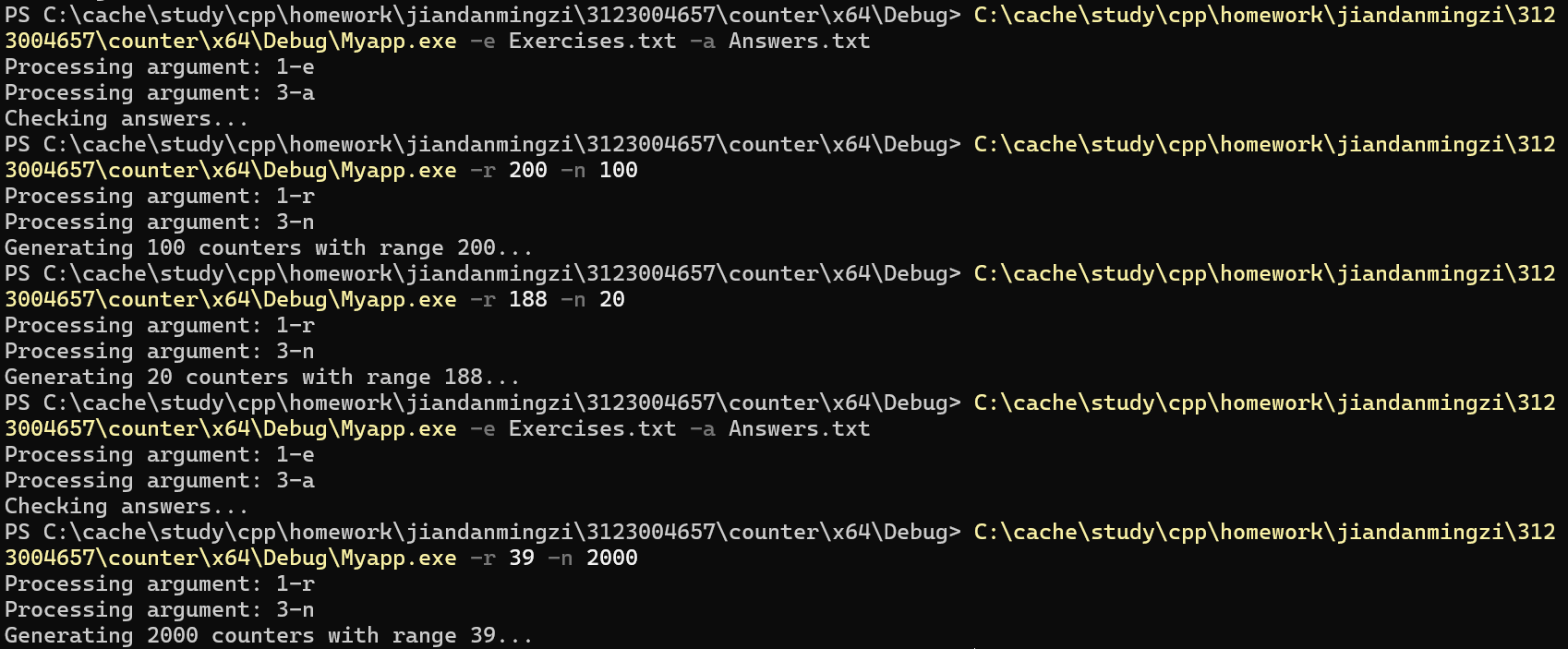
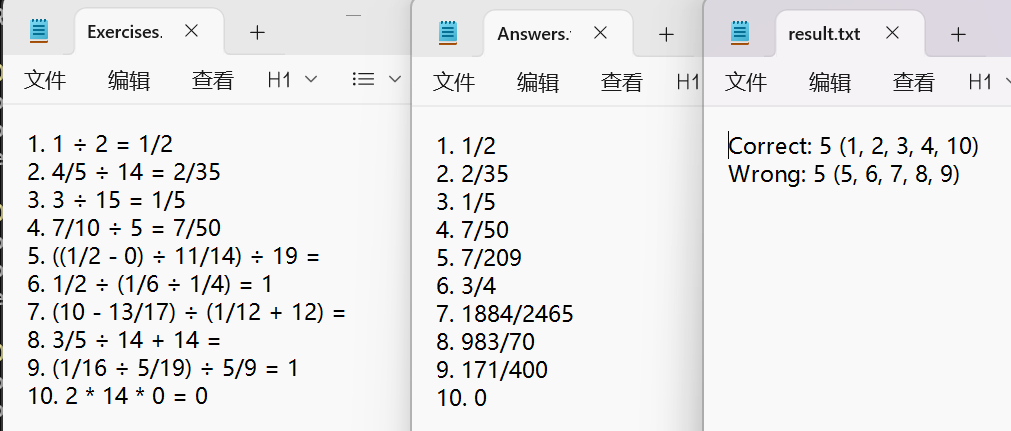
前五次测试的输出结果(生成的txt文件截图)


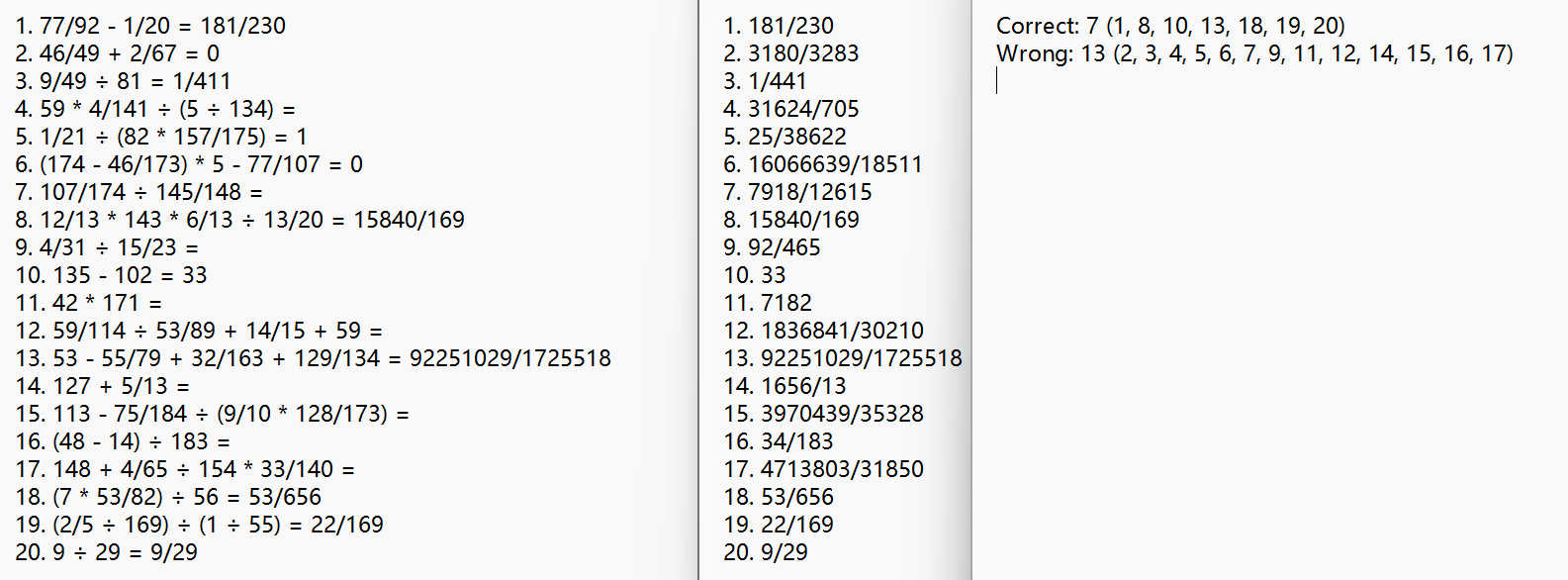
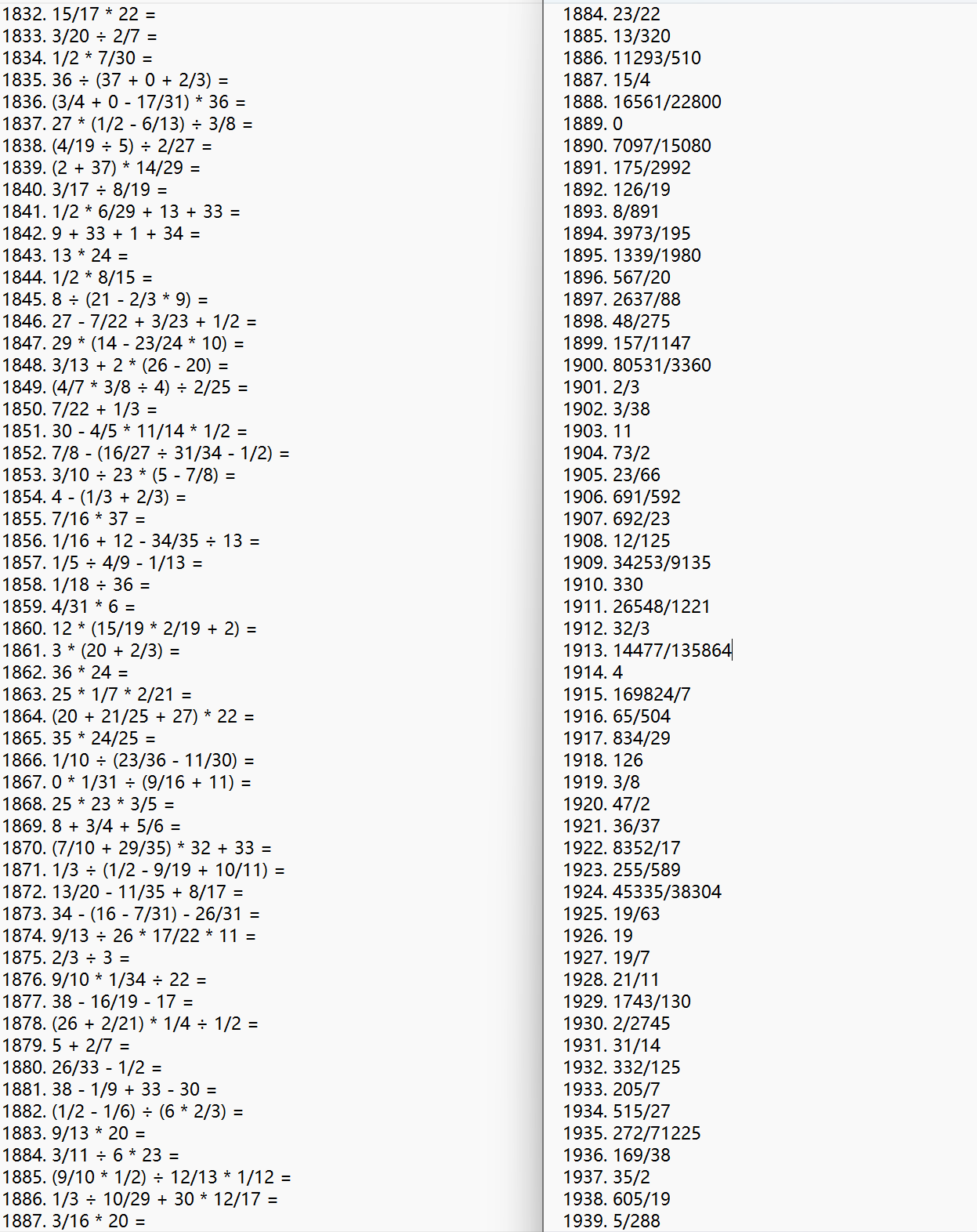
后五次测试输入的参数:
后五次测试的输出结果(生成的txt文件截图):
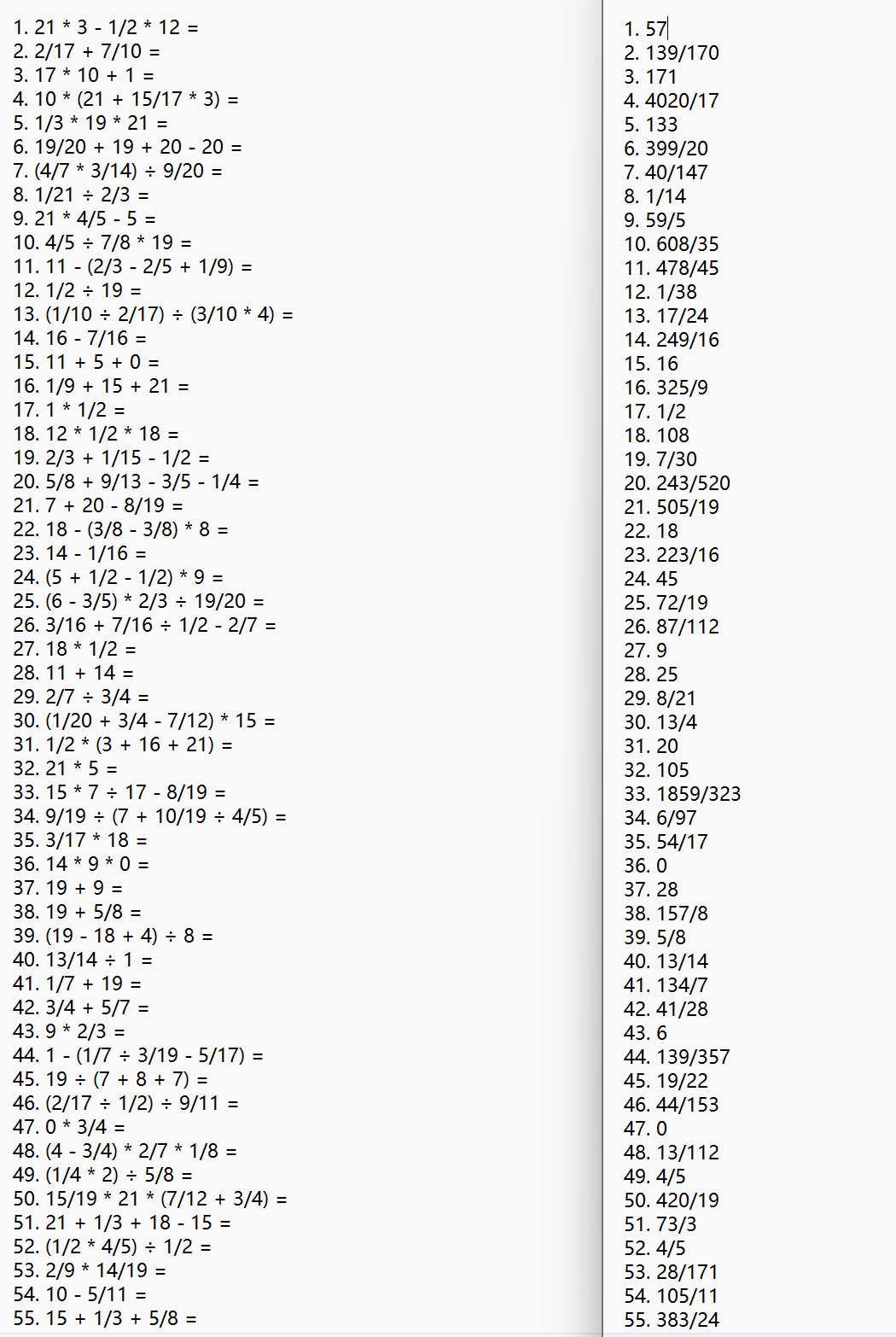



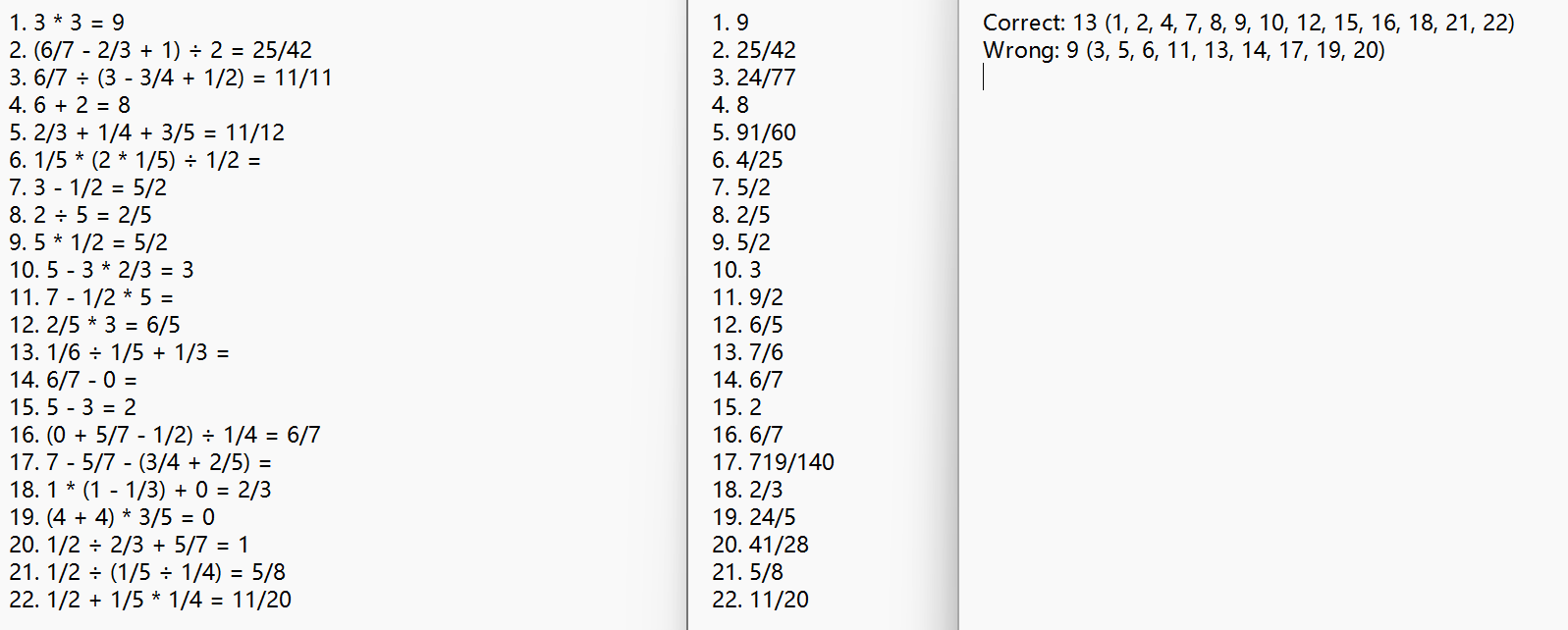
确认程序正确的原因:
截图中的所有四则运算均经过人工检查,确认符合题目需求
截图中的所有四则运算均人工进行了计算,得出的结果与程序给出的答案一致
检验答案产生的结果经过人工对照,完全符合现实
5. PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 40 | 34 |
| Estimate | 估计这个任务需要多少时间 | 15 | 1 |
| Development | 开发 | 360 | 400 |
| Analysis | 需求分析 (包括学习新技术) | 30 | 60 |
| Design Spec | 生成设计文档 | 30 | 20 |
| Design Review | 设计复审 | 20 | 10 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 20 | 30 |
| Design | 具体设计 | 30 | 40 |
| Coding | 具体编码 | 20 | 10 |
| Code Review | 代码复审 | 30 | 45 |
| Test | 测试(自我测试,修改代码,提交修改) | 50 | 60 |
| Reporting | 报告 | 60 | 63 |
| Test Repor | 测试报告 | 25 | 15 |
| Size Measurement | 计算工作量 | 5 | 8 |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 10 | 15 |
| 合计 | 745 | 811 |
6.小结
结对感受:设置github允许别人上传过程复杂,因为第一次结对开发,两人对git的共同开发使用也不是很熟练,分工后也因为完成设计途中发现原设计有问题然后修改设计方案导致分工出问题,又因为开始码代码的时间较晚,所以最终采用了两人分开时间开发,一方开发完成后将新文件发给另一方这种低效的形式进行开发;因此,下次开发前,要学习并熟练掌握git的多人开发,同时在设计的时候去查证拟定的开发思路是否有问题。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号