BUAA_OO_Unit1总结
总体架构
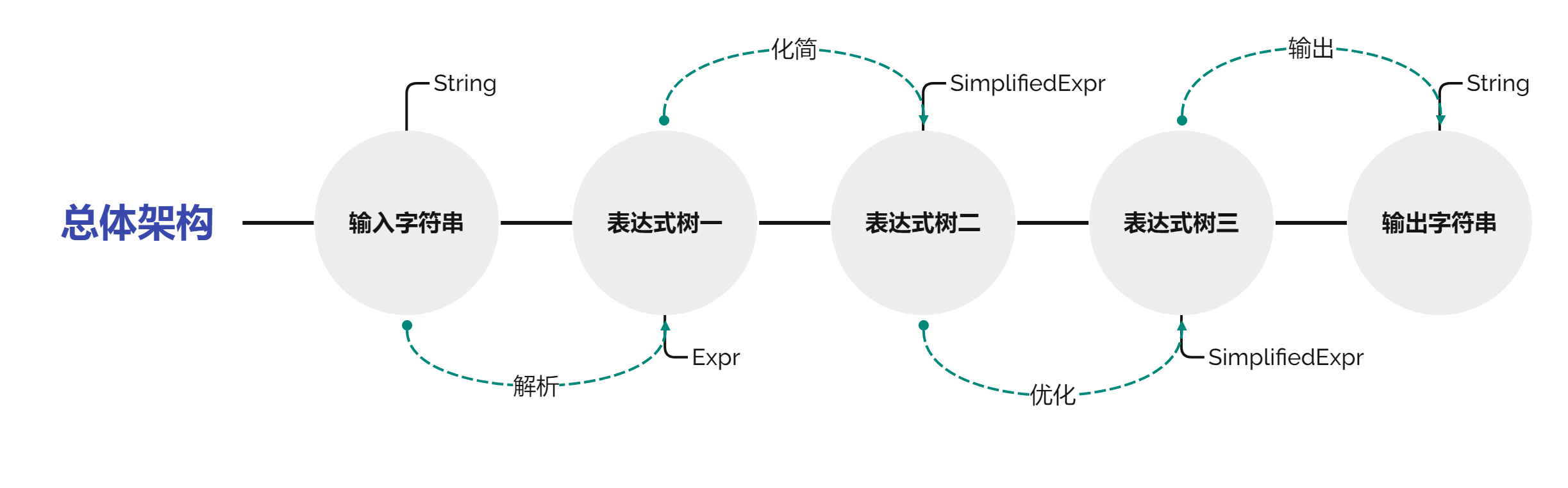
经过完成本单元的三次作业,我提炼出了上面这一总体架构,三次作业都遵循这一总体架构,下面对这一架构进行简单的解释,详细见各个作业中的分析。
-
-
输入字符串(String)
输入字符串为原始输入的数据,未经任何处理。
-
表达式树一(Expr)
表达式树一中表达式为树形结构,但其中包含非必要的括号,不满足题目要求。
-
表达式树二(SimplifiedExpr)
表达式树二中表达式为树形结构,其中只包含必要的括号,但长度性能较差。
-
表达式树三(SimplifiedExpr)
表达式树三中表达式为树形结构,且长度性能较优。
-
输出字符串(String)
输出字符串为最终输出的数据。
-
-
方法
-
解析(parse)
使用递归下降的方法将线性结构(输入字符串)解析为树形结构(表达式树一)。此时表达式树一中包含非必要的括号,暂且不满足题目的要求,还需进一步化简。
-
化简(simplify)
使用递归下降的方法将表达式树一化简为表达式树二。将表达式树一非必要的括号去掉,此外,若两因子可合并,则将指数相加合并为同一因子;若两项可合并,则将系数相加合并为同一项。此时表达式树二中只含必要的括号,满足题目的要求,但长度性能较差,还需进一步优化。
-
优化(optimize)
使用递归下降的方法将表达式树二优化为表达式树三。利用三角函数公式对表达式优化使得长度尽可能的短。此时,表达式树三长度得到了减少,满足题目的要求,但仍为树形结构,还需进一步输出。
-
输出(toString)
使用递归下降的方法将树形结构(表达式树三)输出为线性结构(输出字符串)。
-
hw1
-
总览
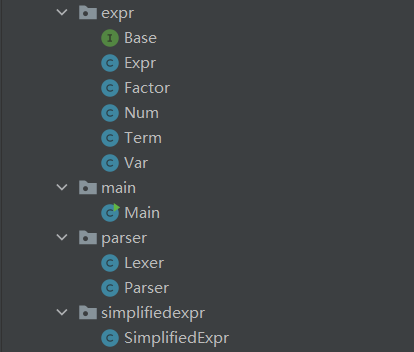
-
数据
-
Expr
-
SimplifiedExpr

-
-
方法
-
解析(parse)
在Parser类中,对输入的字符串进行递归下降的解析,形成表达式树。
-
化简(simplify)
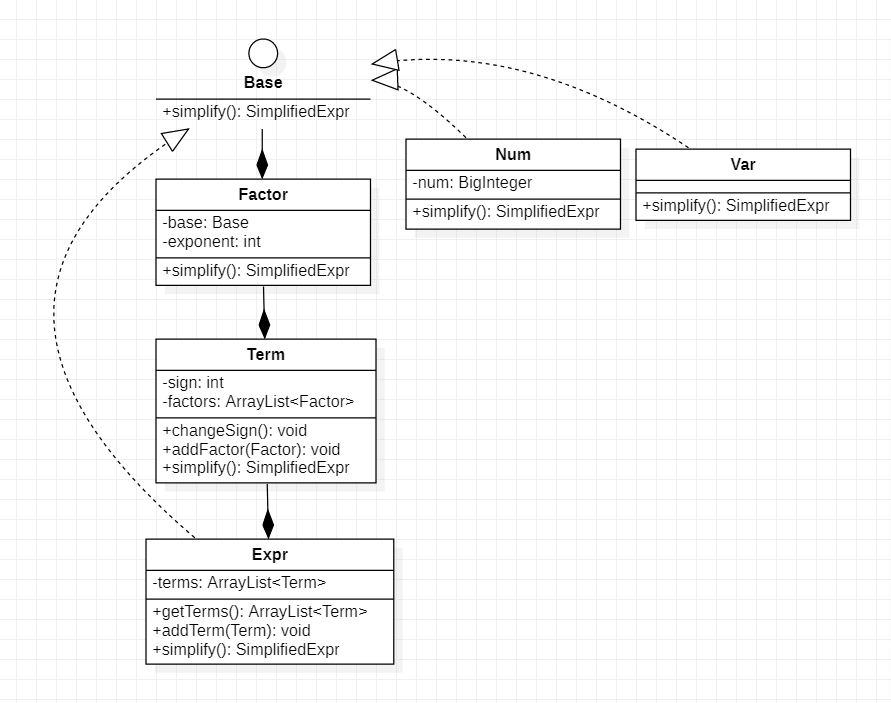
从上面的类图中可以看到,在Expr相关的类中都有simplify这一方法可以将本类的数据转换为SimplifiedExpr这一类型,SimplifiedExpr实际上为一个哈希表的结构,key为指数,value为系数。以下是各类中simplify方法的具体实现:
-
Expr
将各个Term所产生的SimplifiedExpr相加得到一个新的SimplifiedExpr。
-
Term
将各个Factor所产生的SimplifiedExpr相乘得到一个新的SimplifiedExpr。
-
Factor
将Base所产生的SimplifiedExpr进行次方运算得到一个新的SimplifiedExpr。
-
Var
SimplifiedExpr中有一个键值对key:1 value:1。
-
Num
SimplifiedExpr中有一个键值对key:0 value:num。
-
-
优化(optimize)
因为hw1中只有常量因子和幂函数因子,所以不能够进一步优化,此步骤省略。
-
输出(toString)
SimplifiedExpr这一类型中有toString的方法,将SimplifiedExpr转换为String,并进行一定的长度优化:
-
指数为0,1,2
-
系数为0,1,-1
-
第一项的符号为正
-
-
-
例子
-
输入字符串
-4*x**3*x**2+(x*x**2+1)**2
-
表达式树一
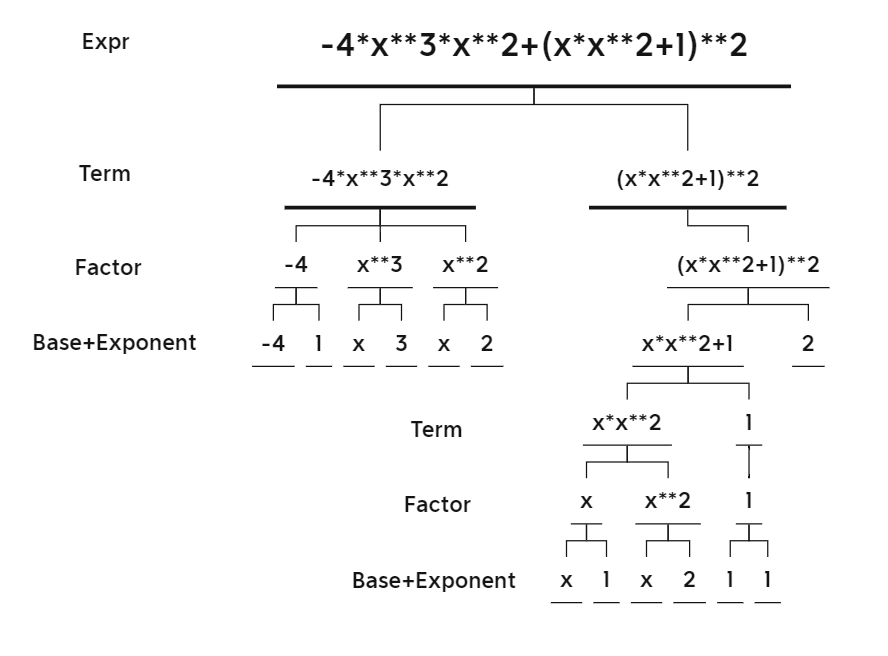
-
表达式树二
exponent 0 1 2 3 4 5 6 7 8 coefficient 1 0 0 2 0 -4 1 0 0 -
表达式树三
无
-
输出字符串
x**6-4*x**5+2*x**3+1
-
-
度量
-
数据
Method CogC ev(G) iv(G) v(G) expr.Expr.Expr() 0 1 1 1 expr.Expr.addTerm(Term) 0 1 1 1 expr.Expr.getTerms() 0 1 1 1 expr.Expr.simplify() 1 1 2 2 expr.Factor.Factor(Base, int) 0 1 1 1 expr.Factor.simplify() 0 1 1 1 expr.Num.Num(BigInteger) 0 1 1 1 expr.Num.simplify() 0 1 1 1 expr.Term.Term() 0 1 1 1 expr.Term.addFactor(Factor) 0 1 1 1 expr.Term.changeSign() 0 1 1 1 expr.Term.simplify() 2 1 3 3 expr.Var.simplify() 0 1 1 1 main.Main.main(String[]) 0 1 1 1 parser.Lexer.Lexer(String) 0 1 1 1 parser.Lexer.getCurToken() 0 1 1 1 parser.Lexer.getNumber() 2 1 3 3 parser.Lexer.next() 3 2 3 4 parser.Parser.Parser(Lexer) 0 1 1 1 parser.Parser.parseBase() 3 1 3 3 parser.Parser.parseExponent() 3 1 3 3 parser.Parser.parseExpr() 8 1 7 7 parser.Parser.parseFactor() 0 1 1 1 parser.Parser.parseNum() 5 1 4 5 parser.Parser.parseTerm() 4 1 4 4 parser.Parser.parseVar() 0 1 1 1 simplifiedexpr.SimplifiedExpr.SimplifiedExpr() 0 1 1 1 simplifiedexpr.SimplifiedExpr.add(SimplifiedExpr) 1 1 2 2 simplifiedexpr.SimplifiedExpr.getCoefficients() 0 1 1 1 simplifiedexpr.SimplifiedExpr.multiply(SimplifiedExpr) 6 1 4 4 simplifiedexpr.SimplifiedExpr.negate() 1 1 2 2 simplifiedexpr.SimplifiedExpr.pow(int) 1 1 2 2 simplifiedexpr.SimplifiedExpr.toString() 9 3 7 8 Class OCavg OCmax WMC expr.Expr 1.25 2 5 expr.Factor 1 1 2 expr.Num 1 1 2 expr.Term 1.5 3 6 expr.Var 1 1 1 main.Main 1 1 1 parser.Lexer 2 4 8 parser.Parser 2.88 6 23 simplifiedexpr.SimplifiedExpr 2.71 7 19 -
分析
第一次作业较为简单,所以方法和类的复杂度并不高。
- 代码行数

-
bug分析
hw1的难度较为简单,所以并没有出现bug。
hw2 hw3
我在hw2与hw3的架构大致相同,所以放在一起来解释。
-
总览
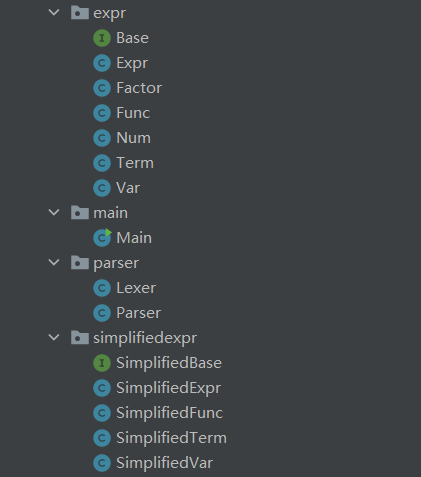
-
数据
-
Expr
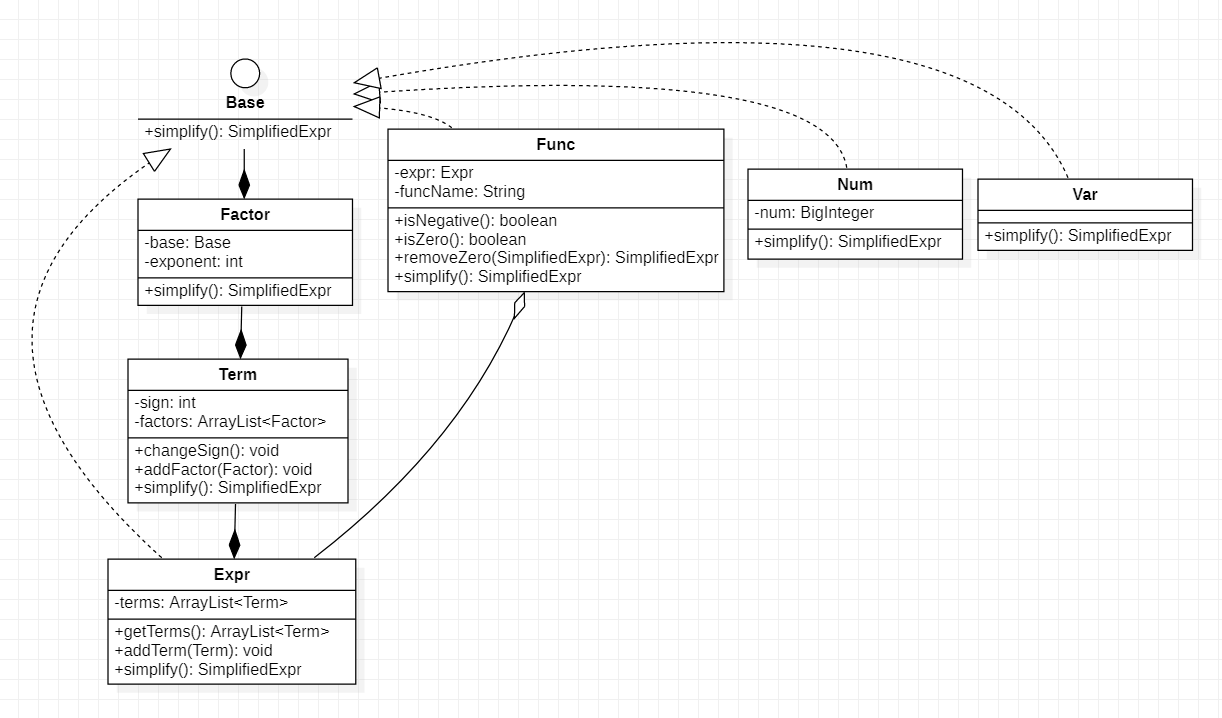
-
SimplifiedExpr
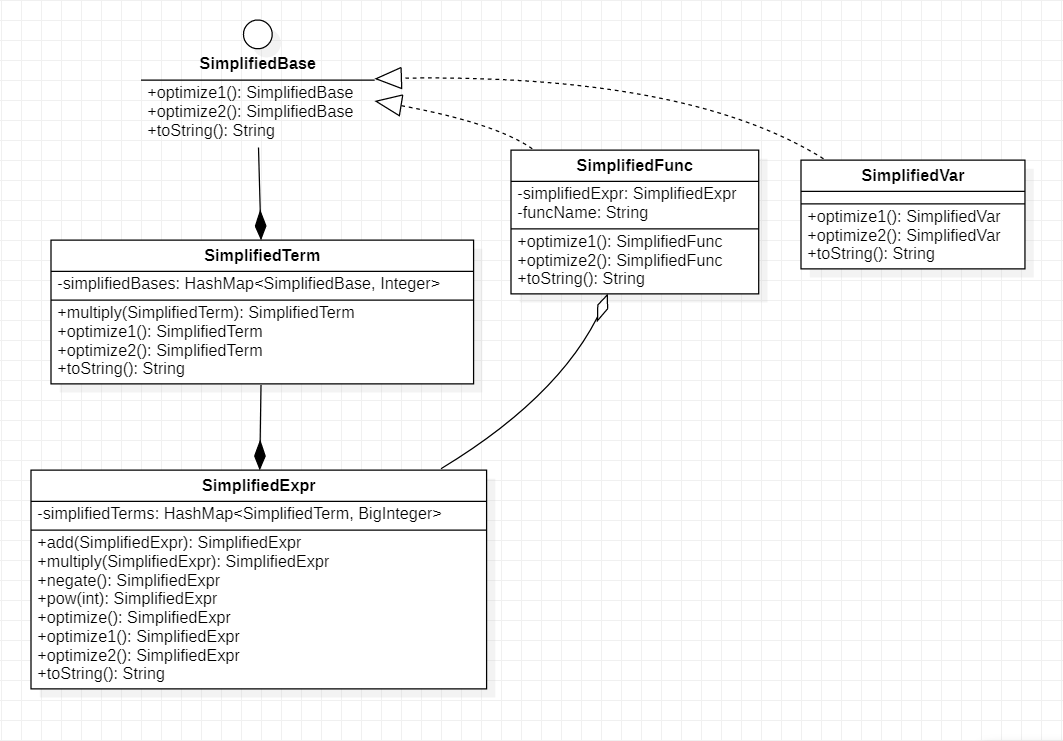
-
-
方法
-
解析(parse)
在Parser类中,对输入的字符串进行递归下降的解析,形成表达式树。
-
化简(simplify)
从上面的类图中可以看到,在Expr相关的类中都有simplify这一方法可以将本类的数据转换为SimplifiedExpr这一类型,SimplifiedExpr的具体结果如上,以下是各类中simplify方法的具体实现:
-
Expr
将各个Term所产生的SimplifiedExpr相加得到一个新的SimplifiedExpr。
-
Term
将各个Factor所产生的SimplifiedExpr相乘得到一个新的SimplifiedExpr。
-
Factor
将Base所产生的SimplifiedExpr进行次方运算得到一个新的SimplifiedExpr。
-
Var
SimplifiedExpr中只有x这一项。
-
Num
SimplifiedExpr中只有num这一项。
-
Func
将Func中的Expr进行化简得到SimplifiedExpr,并和FuncName一块封装在SimplifiedFunc中,得到新的SimplifiedExpr。
-
-
优化(optimize)
从上面的类图中可以看到,在SimplifiedExpr相关的类中都有optimize这一方法利用三角函数公式进行长度优化:
-
sin、cos中的表达式第一项符号为正
-
sin²和cos²合并
-
二倍角公式
不难发现,优化的顺序以及次数都会影响到最终的结果,为了得到最优的结果,可以重复调用这些优化的方法直到输出的长度不再变化。
-
-
输出(toString)
从上面的类图中可以看到,在SimplifiedExpr相关的类中都有toString的方法可以将本类的数据转换为String,并进行一定的长度优化:
-
指数为0,1,2
-
系数为0,1,-1
-
第一项的符号为正
-
-
-
例子
-
输入字符串
x*sin((2*x))*2*sin(x)*cos(x)+(x+1)*cos((2*x))**2-cos((2*x))**2
-
表达式树一
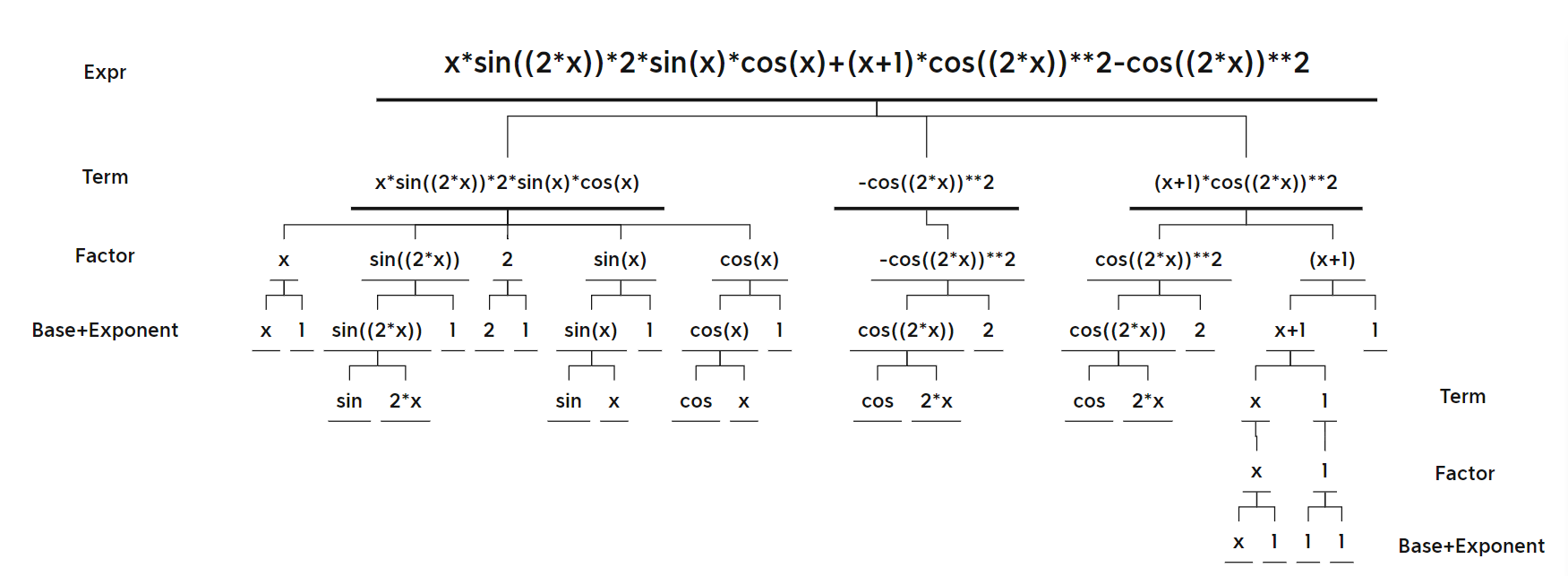
-
表达式树二
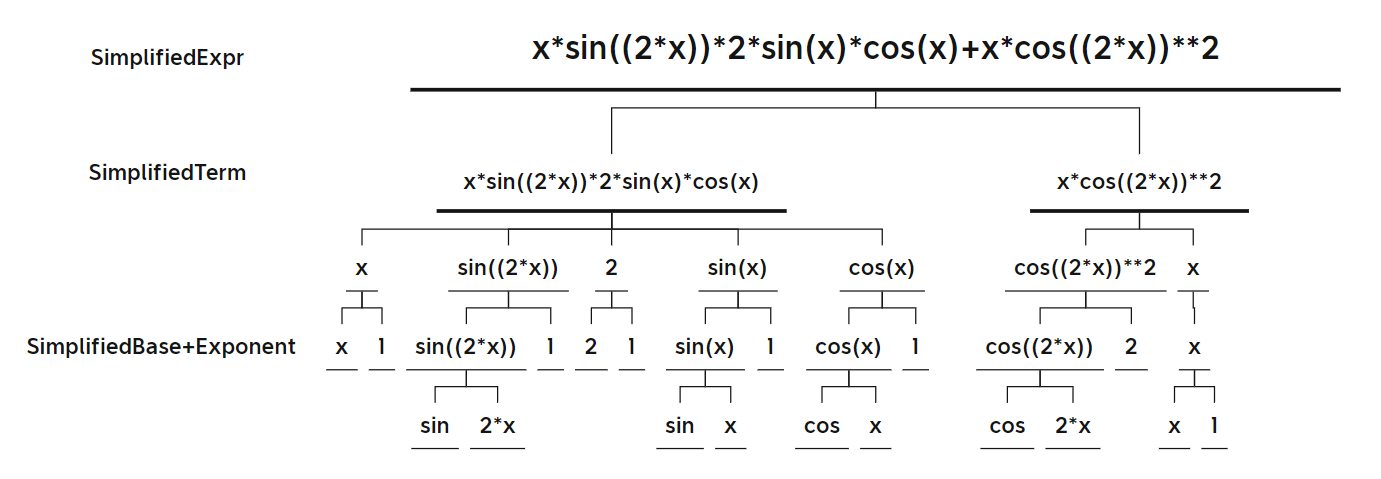
-
表达式树三
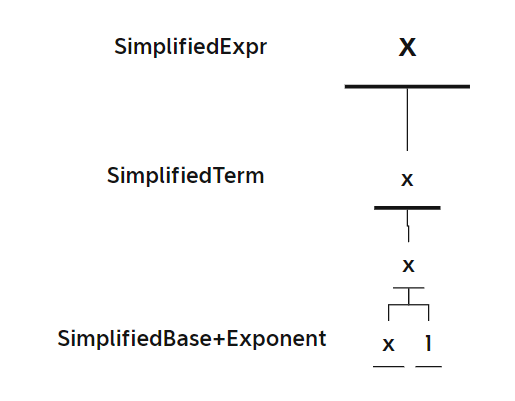
-
输出字符串
x
-
-
度量
-
数据
Method CogC ev(G) iv(G) v(G) simplifiedexpr.SimplifiedTerm.optimize2(SimplifiedExpr) 21 5 10 11 simplifiedexpr.SimplifiedExpr.toString() 15 3 9 10 simplifiedexpr.SimplifiedExpr.merge() 44 8 11 13 simplifiedexpr.SimplifiedExpr.func2(BigInteger, BigInteger, SimplifiedTerm, SimplifiedTerm, SimplifiedTerm, SimplifiedTerm) 14 1 11 11 parser.Lexer.getFuncName() 17 1 7 9 expr.Func.isNegative() 4 4 3 4 Class OCavg OCmax WMC expr.Func 3.4 6 17 parser.Lexer 3.2 7 16 parser.Parser 3.36 7 37 simplifiedexpr.SimplifiedExpr 3.25 11 52 simplifiedexpr.SimplifiedTerm 3.3 8 33
-
分析
第二三次作业中,复杂度主要来自于两个方面,解析和优化。解析时会出现大量的if语句来对字符串进行解析。优化时也会出现大量的for以及if来进行三角函数公式的优化。
- 代码行数
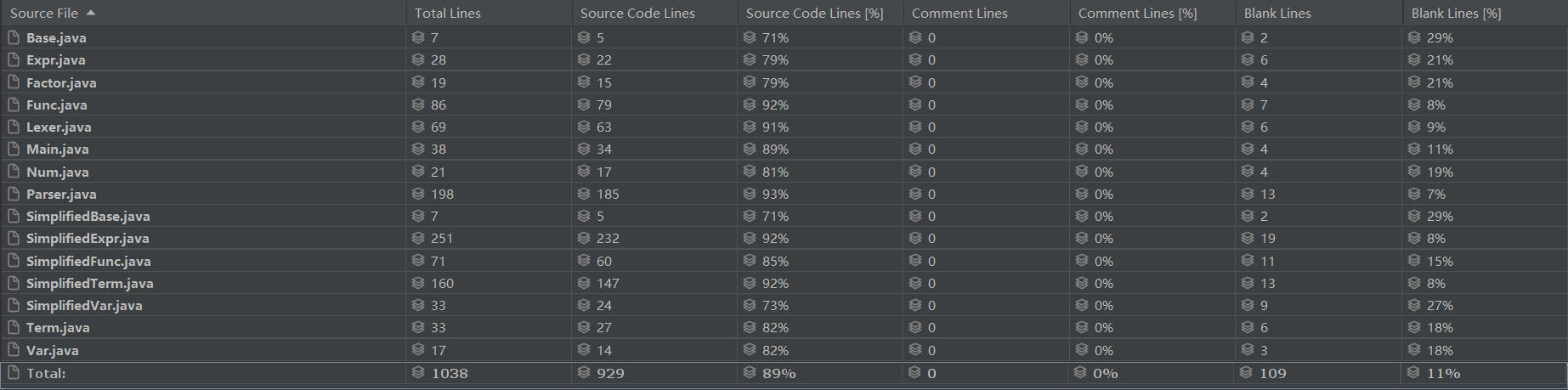
-
-
bug分析
-
自己
我的程序再中测、互测、强测中均没有bug,但在自己刚刚把代码写完时还是有一些bug的:
-
深拷贝和浅拷贝
因为在本次作业中使用到了HashMap这一容器,如果对容器中的内容浅拷贝并进行了修改那么就会产生bug,好在这一bug容易发现,再运行了几个测试数据后就会产生空指针的异常。解决方法是使用深拷贝,我的深拷贝是在构造函数中实现的,类似于C++中的拷贝构造函数。
-
同类型的合并
我在刚写完代码时,如果输入2*sin(x)*cos(x)*sin((2*x))这一样例,则会输出sin((2*x)),但实际上应该输出sin((2*x))**2,原因是我在将2*sin(x)*cos(x)合并后并没有考虑容器内是否有sin((2*x)),如果有的话需要将指数相加。
这些bug主要存在于代码复杂度较高的区域。
-
-
他人
对于别人的代码我只发现了一个bug:
-
类型问题
sum中的第2、3项有人使用了int进行存储,但实际上会超出long的范围,所以应该用BigInteger进行存储。
-
-
总结
-
架构优缺点
-
优点
-
将整个问题分为四个步骤:解析、化简、优化、输出,使得逻辑更加清晰。
-
采用了两套数据结构:Expr、SimplifiedExpr,使得各个类的复杂度降低。
-
-
缺点
-
在三角函数公式的优化上复杂度较高,容易产生bug。
-
两套数据结构并无本质的差异,都是在存储表达式,实际上可以简化为一套数据结构。
-
-
-
心得体会
-
化繁为简
当我们面临一个复杂的工程时,可以将这一复杂的工程进行适当的简化,并在此基础上进行迭代开发,逐步解决复杂工程。正如本单元的表达式化简,如果我们直接去思考hw3,那必然会非常痛苦,但是我们按照hw1到hw3的顺序进行迭代开发,则会简单很多。
-
及时重构
当我们需要对工程的功能进行扩展时,如果我们当前的架构已经不能实现该功能,或者我们为了实现这一功能导致架构很不优雅,这时我们就需要及时对我们的架构进行重构,设计出一个更好的架构。正如我在本单元的架构中使用了两套数据结构,分别为Expr和SimplifiedExpr,实际上可以将两者进行合并从而使用一套数据结构即可。
-
重设计轻实现
我们应把大量的时间花费在设计上,而不是急于实现。当我们设计完成后,我们应该要知道我们的代码可以完成哪些功能、不可以完成哪些功能。实现只是对设计的代码化,个人认为这是一个比较机械的过程。如果并没有完成设计就开始了代码实现,此时思路并不清晰,极易出现bug,而且当这一设计走不通时,代码还要重写。
-
注重OOP思想
-



 浙公网安备 33010602011771号
浙公网安备 33010602011771号