python简述十大排序
小阿杰已经摆烂了很多天了QAQ,今天决定氵一篇新博客(👉👈),用python简单描述一下我们的经典十大排序——
1.选择排序
选择排序(Selection Sort)是一种简单直观的排序算法。它的基本思想是每次从待排序序列中选择一个最小(或最大)的元素,将它与序列中的第一个元素交换位置,然后将剩余未排序部分的最小(或最大)元素找出并放到已排序部分的末尾。通过不断选择最小(或最大)元素,并交换位置,最终完成整个序列的排序。
选择排序的具体步骤如下:
1. 遍历待排序序列,将当前位置设为最小元素的索引。
2. 从当前位置开始,遍历剩余序列,找到最小元素的索引。
3. 如果最小元素的索引不等于当前位置,则交换最小元素与当前位置的元素。
4. 将当前位置后移一位,重复步骤2和步骤3直至遍历完整个序列。
1 #选择排序 2 def selection_sort(arr): 3 n = len(arr) 4 for i in range(n-1): # 进行 n-1 轮选择 5 min_index = i 6 for j in range(i+1, n): 7 if arr[j] < arr[min_index]: 8 min_index = j 9 arr[i], arr[min_index] = arr[min_index], arr[i] # 交换最小元素到当前位置 10 return arr 11 12 # 示例 13 arr = [64, 25, 12, 22, 11] 14 sorted_arr = selection_sort(arr) 15 print("排序后的数组:", sorted_arr)
2.插入排序
插入排序(Insertion Sort)是一种简单直观的排序算法。它的基本思想是将待排序序列分为已排序部分和未排序部分,每次从未排序部分取出一个元素,在已排序部分中找到合适的位置并插入。通过不断将未排序部分的元素插入到已排序部分,最终完成整个序列的排序。
插入排序的具体步骤如下:
- 将序列的第一个元素视为已排序部分。
- 从序列的第二个元素开始,依次将元素插入到已排序部分的合适位置。
- 每次插入时,将当前元素与已排序部分的元素从后往前逐个比较,直至找到合适的插入位置。
- 插入完成后,已排序部分增加一个元素,未排序部分减少一个元素。
- 重复步骤2至步骤4,直至未排序部分为空。
1 #插入排序 2 def insertion_sort(arr): 3 n = len(arr) 4 for i in range(1, n): 5 key = arr[i] # 当前要插入的元素 6 j = i - 1 # 已排序部分的最后一个元素 7 8 # 将比当前元素大的元素向后移动,为当前元素腾出插入位置 9 while j >= 0 and arr[j] > key: 10 arr[j + 1] = arr[j] 11 j -= 1 12 13 arr[j + 1] = key 14 15 return arr 16 # 示例 17 arr = [64, 25, 12, 22, 11] 18 sorted_arr = insertion_sort(arr) 19 print("排序后的数组:", sorted_arr)
3.冒泡排序
冒泡排序(Bubble Sort)是一种简单直观的排序算法。它的基本思想是通过不断比较相邻元素的大小,将较大的元素逐步交换到末尾,从而使得序列中最大的元素不断冒泡到最后。通过多次冒泡操作,最终完成整个序列的排序。
冒泡排序的具体步骤如下:
- 从序列的第一个元素开始,依次比较相邻的两个元素的大小。
- 如果前一个元素大于后一个元素,则交换这两个元素的位置,使较大的元素向后移动一位。
- 继续按照上述方式比较剩余的相邻元素,不断进行交换操作,直至将最大的元素冒泡到序列末尾。
- 重复步骤1至步骤3,每次比较的元素数量减少1。
1 #冒泡排序 2 def bubble_sort(arr): 3 n = len(arr) 4 for i in range(n-1): 5 for j in range(n-i-1): 6 if arr[j] > arr[j+1]: 7 arr[j], arr[j+1] = arr[j+1], arr[j] # 交换顺序 8 return arr 9 # 示例 10 arr = [64, 25, 12, 22, 11] 11 sorted_arr = bubble_sort(arr) 12 print("排序后的数组:", sorted_arr)
4.归并排序
归并排序(Merge Sort)是一种经典的排序算法,它使用分治法(Divide and Conquer)的思想。它将待排序的数组不断地分成两半,直到每个子数组都只有一个元素,然后将这些单个元素的子数组合并成一个有序的数组,最终得到排好序的结果。
归并排序的主要思想是将数组递归地分成两半,对每个子数组进行排序,然后再将两个有序的子数组合并成一个有序的数组。这个过程不断地重复,直到整个数组排序完成。具体步骤如下:
-
分割:将待排序的数组分成两个子数组,中间位置为分界点。可以采用递归的方式对子数组也进行分割,直到每个子数组只有一个元素。
-
合并:从单个元素的子数组开始,将相邻的两个子数组合并成一个有序的数组。合并过程中,比较两个子数组的第一个元素,将较小的元素放入新的数组中,并移动指针。重复这个过程,直到将所有元素合并到一个大的有序数组中。
-
重复以上两个步骤,直到整个数组排序完成。
1 #归并排序 2 def merge_sort(arr): 3 # 递归结束条件:数组长度为1时,无需再分割 4 if len(arr) <= 1: 5 return arr 6 7 # 将数组一分为二 8 mid = len(arr) // 2 9 left_half = arr[:mid] 10 right_half = arr[mid:] 11 12 # 递归调用归并排序函数,对两个子数组进行排序 13 left_half = merge_sort(left_half) 14 right_half = merge_sort(right_half) 15 16 # 合并两个有序子数组 17 sorted_arr = merge(left_half, right_half) 18 return sorted_arr 19 20 21 def merge(left, right): 22 merged = [] 23 left_index, right_index = 0, 0 24 25 # 依次比较两个子数组的元素,将较小的元素放入新数组中 26 while left_index < len(left) and right_index < len(right): 27 if left[left_index] < right[right_index]: 28 merged.append(left[left_index]) 29 left_index += 1 30 else: 31 merged.append(right[right_index]) 32 right_index += 1 33 34 # 将剩余未加入新数组的元素加入 35 merged.extend(left[left_index:]) 36 merged.extend(right[right_index:]) 37 38 return merged 39 arr = [5, 2, 8, 1, 9, 3] 40 sorted_arr = merge_sort(arr) 41 print(sorted_arr) # 输出结果为 [1, 2, 3, 5, 8, 9]
5.快速排序
快速排序(Quick Sort)是一种常用且高效的排序算法,也属于分治法(Divide and Conquer)的一种应用。它通过选择一个基准元素,将数组分为两个子数组,一个子数组中的元素小于等于基准元素,另一个子数组中的元素大于基准元素,然后对这两个子数组进行递归排序,最终得到有序的结果。
快速排序的基本思想是选择一个基准元素,然后根据该元素将待排序数组划分为小于等于基准元素的部分和大于基准元素的部分。具体步骤如下:
-
选择基准元素:从待排序数组中选择一个元素作为基准元素(通常选择第一个或最后一个元素)。
-
划分:将数组中小于等于基准元素的元素放在基准元素的左边,大于基准元素的元素放在基准元素的右边。这个过程称为划分(Partitioning),可以使用多种方法实现,其中一种常见的方法是使用双指针(i 和 j)。
-
递归排序:对基准元素左右两边的子数组进行递归排序,即重复上述步骤,直到每个子数组只有一个元素。
-
合并:将左右两个子数组合并,即将左边的子数组、基准元素、右边的子数组按顺序连接起来,得到有序的数组。
1 #快速排序 2 def quick_sort(arr): 3 if len(arr) <= 1: 4 return arr 5 6 # 选择基准元素 7 pivot = arr[0] 8 9 # 将小于基准元素的放在左边,大于基准元素的放在右边 10 left = [x for x in arr[1:] if x <= pivot] 11 right = [x for x in arr[1:] if x > pivot] 12 13 # 递归调用快速排序函数,对左右两个子数组进行排序 14 left = quick_sort(left) 15 right = quick_sort(right) 16 17 # 合并左右两个子数组和基准元素 18 return left + [pivot] + right 19 arr = [5, 2, 8, 1, 9, 3] 20 sorted_arr = quick_sort(arr) 21 print(sorted_arr) # 输出结果为 [1, 2, 3, 5, 8, 9]
6.希尔排序
希尔排序(Shell Sort),也称为“缩小增量排序”,是一种改进的插入排序算法。它通过将待排序的数组按照一定的间隔进行分组,对每个分组使用插入排序算法进行排序,逐渐减小间隔,直到间隔为1,最后进行一次完整的插入排序,从而得到有序的结果。
希尔排序的主要思想是先将数组按照一定的间隔进行分组,对每个分组进行插入排序,然后逐渐缩小间隔,重复这个过程,直到间隔为1。具体步骤如下:
-
选择增量序列:选定一个增量序列,例如希尔增量序列(Shell's Gap Sequence),通常以3倍递减的方式选择。增量序列决定了分组的间隔。
-
分组排序:根据选定的增量序列,将待排序数组分成多个子数组,每个子数组包含同样间隔的元素。对每个子数组应用插入排序算法进行排序。
-
缩小间隔:逐渐缩小增量,再次将数组分成多个子数组,对每个子数组进行插入排序。重复这个过程,直到增量缩小到1。
-
最终排序:当增量缩小到1时,进行一次完整的插入排序,此时数组中的元素已经基本有序,插入排序的效率较高。
1 #希尔排序 2 def shell_sort(arr): 3 n = len(arr) 4 gap = n // 2 # 初始化增量值 5 6 while gap > 0: 7 # 对每个子序列进行插入排序 8 for i in range(gap, n): 9 temp = arr[i] 10 j = i 11 12 # 在当前子序列中进行插入排序 13 while j >= gap and arr[j - gap] > temp: 14 arr[j] = arr[j - gap] 15 j -= gap 16 17 arr[j] = temp 18 19 gap //= 2 # 缩小增量值 20 # 使用示例 21 arr = [9, 5, 8, 1, 2, 3] 22 shell_sort(arr) 23 print(arr) # 输出结果为 [1, 2, 3, 5, 8, 9]
7.堆排序
堆排序(Heap Sort)是一种基于完全二叉堆的排序算法,它利用堆的特性进行排序操作。堆是一种完全二叉树,可以分为最大堆和最小堆两种形式。在堆排序中,我们通常使用最大堆。
堆排序主要思想是将待排序的数组构建成一个最大堆,然后将堆顶元素与堆尾元素交换,再对剩余的堆进行调整,重复这个过程,直到整个数组有序。
具体步骤如下:
-
构建最大堆:将待排序的数组看作一个完全二叉树,并通过一系列的比较与交换操作,将其转换为一个最大堆。构建最大堆的过程可以采用自底向上的方式,从最后一个非叶子节点开始向上调整。
-
堆排序:将堆顶元素与堆尾元素交换,将最大元素放到数组末尾;然后对剩余的堆进行调整,使其满足最大堆的性质。重复这个过程,直到整个数组有序。
1 #堆排序 2 # 对堆中的某个节点进行调整,使其满足最大堆的性质 3 def heapify(arr, n, i): 4 largest = i # 最大值的索引 5 left = 2 * i + 1 # 左子节点的索引 6 right = 2 * i + 2 # 右子节点的索引 7 8 # 比较左子节点和根节点的值,更新最大值索引 9 if left < n and arr[left] > arr[largest]: 10 largest = left 11 12 # 比较右子节点和当前最大值的值,更新最大值索引 13 if right < n and arr[right] > arr[largest]: 14 largest = right 15 16 # 如果最大值的索引不是当前节点的索引,交换节点的值,并递归调整它所在的子树 17 if largest != i: 18 arr[i], arr[largest] = arr[largest], arr[i] 19 heapify(arr, n, largest) 20 21 # 堆排序算法 22 def heap_sort(arr): 23 n = len(arr) # 序列的长度 24 25 # 构建最大堆,从最后一个非叶子节点开始,逐个向前调整节点 26 for i in range(n // 2 - 1, -1, -1): 27 heapify(arr, n, i) 28 29 # 逐个将堆顶元素(最大值)与末尾元素交换,并重新调整堆 30 for i in range(n - 1, 0, -1): 31 arr[0], arr[i] = arr[i], arr[0] # 将最大值放到序列的末尾 32 heapify(arr, i, 0) # 调整剩余元素为最大堆 33 34 return arr 35 # 使用示例 36 arr = [5, 2, 8, 1, 9, 3] 37 sorted_arr = heap_sort(arr) 38 print(sorted_arr) # 输出结果为 [1, 2, 3, 5, 8, 9]
8.计数排序
计数排序(Counting Sort)是一种线性时间复杂度的非比较排序算法。它通过统计每个元素在待排序序列中出现的次数,然后根据计数信息将元素放回正确的位置上,从而实现排序。
计数排序的基本思想是假设待排序的数组中元素都属于一个确定的范围,并且范围内的元素个数是已知的。根据这个假设,我们可以使用额外的计数数组来统计每个元素出现的次数,然后再根据计数数组重新构造有序的结果。
具体步骤如下:
-
初始化计数数组:根据待排序数组的范围确定计数数组的长度,将计数数组中的所有元素置为0。
-
统计元素出现次数:遍历待排序数组,统计每个元素出现的次数,并将次数保存到计数数组中。例如,如果待排序数组中的元素为arr[i],则计数数组的下标为arr[i],对应的计数数组值加1。
-
累加计数数组:对计数数组进行累加操作,使得每个位置上的值等于前面所有位置上值的总和。
-
构造有序结果:倒序遍历待排序数组,根据计数数组将元素放回正确的位置上,并更新计数数组的值。每次放置一个元素后,相应的计数数组值减1。
1 def countingSort(arr): 2 n = len(arr) 3 if n <= 1: 4 return arr 5 6 # 获取待排序数组的最大值和最小值 7 min_val, max_val = min(arr), max(arr) 8 9 # 计算计数数组的长度,并初始化为0 10 count_length = max_val - min_val + 1 11 count = [0] * count_length 12 13 # 统计每个元素出现的次数 14 for num in arr: 15 count[num - min_val] += 1 16 17 # 对计数数组进行累加操作 18 for i in range(1, count_length): 19 count[i] += count[i - 1] 20 21 # 构造有序结果数组 22 result = [0] * n 23 for num in reversed(arr): 24 count[num - min_val] -= 1 25 index = count[num - min_val] 26 result[index] = num 27 28 return result 29 30 31 # 测试 32 arr = [4, 2, 2, 8, 3, 3, 1] 33 sorted_arr = countingSort(arr) 34 print("排序后的数组:", sorted_arr
9.基数排序
基数排序(Radix Sort)是一种非比较型的排序算法,它根据元素的每个位上的值进行排序。基数排序的核心思想是从最低有效位(个位)开始,依次对所有元素进行稳定排序,直到最高有效位完成排序。
具体步骤如下:
-
初始化桶:根据待排序数组的最大值确定需要的桶个数,并初始化桶。
-
按位排序:从最低有效位开始遍历待排序数组,将每个元素根据当前位的值放入相应的桶中。
-
收集元素:按顺序将各个桶中的元素收集起来,得到一个部分排序的数组。
-
重复步骤2和3:依次处理下一位,直到最高有效位完成排序得到最终结果。
1 def countingSort(arr, exp): 2 n = len(arr) 3 count = [0] * 10 # 初始化计数数组 4 5 # 统计每个位上的元素个数 6 for i in range(n): 7 index = arr[i] // exp 8 count[index % 10] += 1 9 10 # 对计数数组进行累加操作 11 for i in range(1, 10): 12 count[i] += count[i - 1] 13 14 # 根据当前位的值,将元素放入相应的桶中 15 result = [0] * n 16 for i in range(n - 1, -1, -1): 17 index = arr[i] // exp 18 count[index % 10] -= 1 19 result[count[index % 10]] = arr[i] 20 21 return result 22 23 24 def radixSort(arr): 25 max_val = max(arr) # 获取待排序数组的最大值 26 27 exp = 1 28 while max_val // exp > 0: 29 arr = countingSort(arr, exp) 30 exp *= 10 31 32 return arr 33 34 35 # 测试 36 arr = [170, 45, 75, 90, 802, 24, 2, 66] 37 sorted_arr = radixSort(arr) 38 print("排序后的数组:", sorted_arr
10.桶排序
桶排序(Bucket Sort)是一种排序算法,它将待排序元素划分为不同的区间(桶),对每个桶中的元素进行排序,最后将所有桶中的元素按顺序合并成有序数组。
具体步骤如下:
-
确定桶的个数:根据待排序数组的特性和范围,确定需要的桶的个数。
-
划分元素到桶中:遍历待排序数组,将每个元素划分到相应的桶中。
-
对每个桶中的元素进行排序:可以使用其他排序算法(如插入排序、快速排序等)对每个桶中的元素进行排序。
-
合并桶中的元素:按照桶的顺序依次将各个桶中的元素合并成一个有序数组。
1 def insertionSort(bucket): 2 for i in range(1, len(bucket)): 3 key = bucket[i] 4 j = i - 1 5 while j >= 0 and bucket[j] > key: 6 bucket[j + 1] = bucket[j] 7 j -= 1 8 bucket[j + 1] = key 9 10 11 def bucketSort(arr): 12 n = len(arr) 13 if n <= 1: 14 return arr 15 16 # 确定桶的个数 17 bucket_size = 5 18 min_val, max_val = min(arr), max(arr) 19 bucket_count = (max_val - min_val) // bucket_size + 1 20 21 # 初始化桶 22 buckets = [[] for _ in range(bucket_count)] 23 24 # 将元素划分到桶中 25 for num in arr: 26 index = (num - min_val) // bucket_size 27 buckets[index].append(num) 28 29 # 对每个桶中的元素进行排序 30 for bucket in buckets: 31 insertionSort(bucket) 32 33 # 合并桶中的元素 34 sorted_arr = [] 35 for bucket in buckets: 36 sorted_arr.extend(bucket) 37 38 return sorted_arr 39 40 41 # 测试 42 arr = [29, 15, 28, 4, 17, 19, 25, 37, 16, 43] 43 sorted_arr = bucketSort(arr) 44 print("排序后的数组:", sorted_arr)
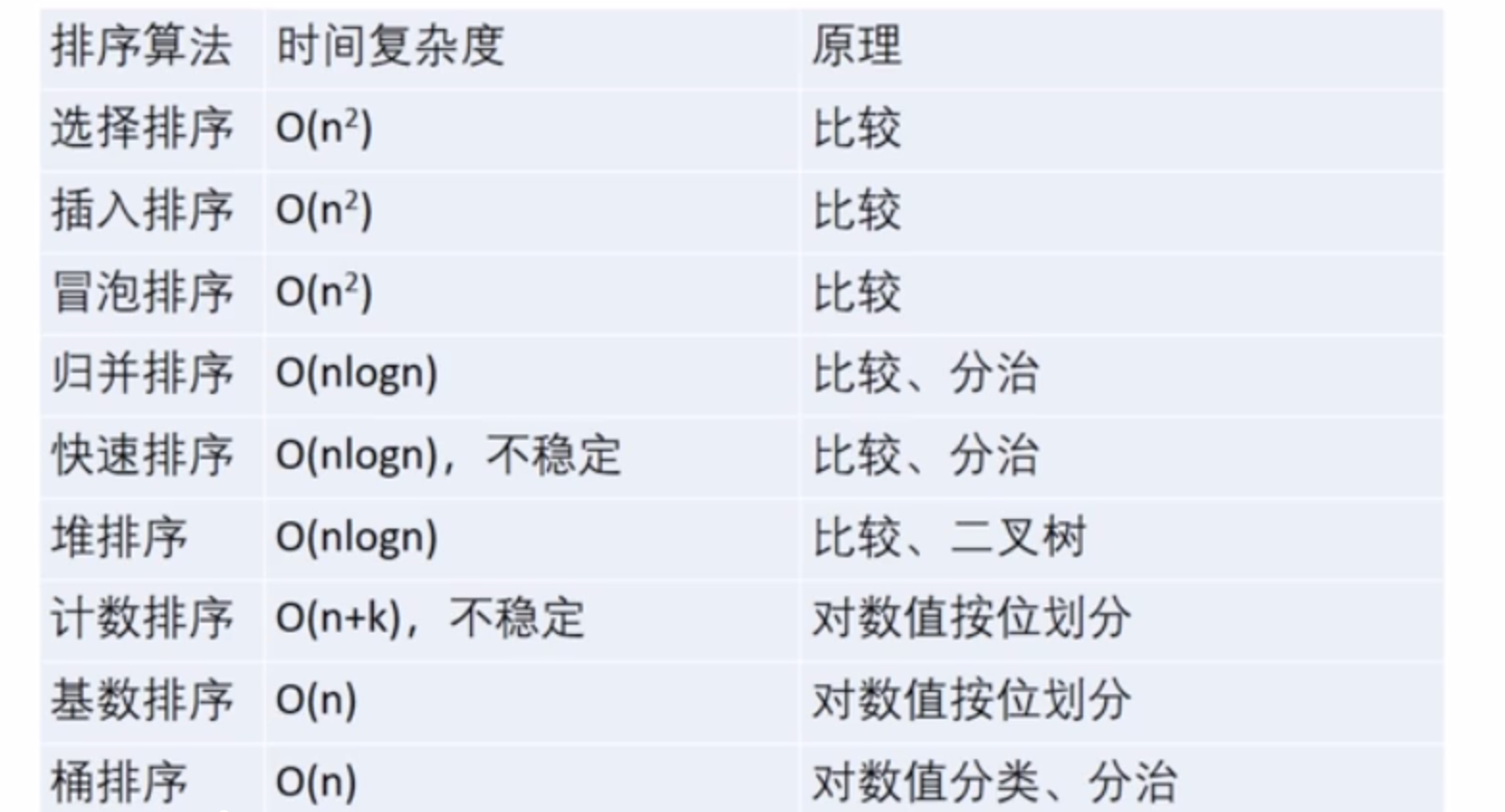
最后附上时间复杂度:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号