5. 动态规划(I)
5.1 背包问题
5.1.1 01 背包问题
题目:有 \(n\) 个物品和一个容量为 \(m\) 的背包,每件物品只能使用一次。第 \(i\) 件物品的体积是 \(v_i\),价值是 \(w_i\)。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大,输出最大价值。\(0<n,m\le 1000,0<v_i,w_i\le 1000\)。
思路:
定义 \(f_{i,j}\) 表示选到前 \(i\) 个物品,背包体积为 \(j\) 时的最大价值。显然初始状态为 \(f_{0,j}=0\),目标状态为 \(f_{n,m}\)。
考虑状态转移:
- 选第 \(i\) 个物品(\(v_i\le j\)):此时的价值为 \(w_i+f_{i-1,j-v_i}\)。
- 不选第 \(i\) 个物品:此时的价值为 \(f_{i-1,j}\)。
所以状态转移方程即为:
注意到每一个状态只与前一个状态有关,所以第一维 \(i\) 可以去掉,\((5.1)\) 变为:
注意,此时需要倒序枚举 \(j\),否则会导致使用已经被更新过的 \(f\) 数组进行计算。
时间复杂度 \(O(nm)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int w[N], v[N];
int f[N];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; ++i) {
for (int j = m; j >= v[i]; --j)
f[j] = max(f[j], w[i]+f[j-v[i]]);
}
printf("%d\n", f[m]);
return 0;
}
5.1.2 完全背包问题
题目:有 \(n\) 个物品和一个容量为 \(m\) 的背包,每件物品可以使用无数次。第 \(i\) 件物品的体积是 \(v_i\),价值是 \(w_i\)。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大,输出最大价值。\(0<n,m\le 1000,0<v_i,w_i\le 1000\)。
思路:
定义 \(f_{i,j}\) 表示选到前 \(i\) 个物品,背包体积为 \(j\) 时的最大价值。显然初始状态为 \(f_{0,j}=0\),目标状态为 \(f_{n,m}\)。
考虑状态转移:
- 选 \(k\;(k>0)\) 件第 \(i\) 个物品(\(kv_i\le j\)):此时的价值为 \(kw_i+f_{i-1,j-kv_i}\)。
- 不选第 \(i\) 个物品:此时的价值为 \(f_{i-1,j}\)。
所以状态转移方程即为:
我们可以发现,对于 \(f_{i,j}\),其实可以用 \(f_{i,j-v_i}\) 来转移。这是因为 \(f_{i,j-v_i}\) 一定是局部最优解,其已经被 \(f_{i,j-2v_i}\) 更新过。\((5.3)\) 可以简化为:
与 01 背包类似,我们可以将第一维 \(i\) 去掉,并且正序枚举 \(j\),则最终的状态转移方程为:
时间复杂度 \(O(nm)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; ++i) {
for (int j = v[i]; j <= m; ++j)
f[j] = max(f[j], w[i]+f[j-v[i]]);
}
printf("%d\n", f[m]);
return 0;
}
5.1.3 多重背包问题
5.1.3.1 朴素多重背包
题目:有 \(n\) 个物品和一个容量为 \(m\) 的背包,每件物品只能使用 \(s_i\) 次。第 \(i\) 件物品的体积是 \(v_i\),价值是 \(w_i\)。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大,输出最大价值。\(0<n,m\le 100,0<v_i,w_i,s_i\le 100\)。
思路:
定义 \(f_{i,j}\) 表示选到前 \(i\) 个物品,背包体积为 \(j\) 时的最大价值。显然初始状态为 \(f_{0,j}=0\),目标状态为 \(f_{n,m}\)。
类似 01 背包和完全背包,其状态转移方程为:
时间复杂度 \(O(nm\sum s_i)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N], s[N], f[N][N];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d%d%d", &v[i], &w[i], &s[i]);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
f[i][j] = f[i-1][j];
for (int k = 1; k <= s[i] && k*v[i] <= j; ++k)
f[i][j] = max(f[i][j], k*w[i]+f[i-1][j-k*v[i]]);
}
}
printf("%d\n", f[n][m]);
return 0;
}
5.1.3.2 二进制优化多重背包
题目:有 \(n\) 个物品和一个容量为 \(m\) 的背包,每件物品只能使用 \(s_i\) 次。第 \(i\) 件物品的体积是 \(v_i\),价值是 \(w_i\)。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大,输出最大价值。\(0<n\le 1000,0<m\le 2000,0<v_i,w_i,s_i\le 2000\)。
思路:
我们可以采用二进制分组的方式。设 \(a_{i,j}\) 表示第 \(i\) 件物品拆成第 \(j\) 组的数量,则 \(a_{i,j}=2^j\)(\(0\le j\le \lfloor\log_2 (s_i+1)\rfloor-1\)),若最后还有余下的物品,则也要将其算作一组。
我们将所有物品拆分完后,再使用 01 背包的方式计算即可。
时间复杂度 \(O(m\sum\log s_i)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
typedef pair<int, int> pii;
const int N = 2010;
int n, m;
int f[N];
vector<pii> goods;
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) {
int v, w, s; scanf("%d%d%d", &v, &w, &s);
int num = 1;
while (s > num) {
goods.push_back({num*v, num*w});
s -= num, num *= 2;
}
if (s) goods.push_back({s*v, s*w});
}
for (auto g : goods) {
int v = g.first, w = g.second;
for (int i = m; i >= v; --i)
f[i] = max(f[i], w+f[i-v]);
}
printf("%d\n", f[m]);
return 0;
}
5.1.4 分组背包问题
题目:有 \(n\) 组物品和一个容量为 \(m\) 的背包,第 \(i\) 组物品有 \(s_i\) 个,其中第 \(j\) 个物品的体积是 \(v_{i,j}\),价值是 \(w_{i,j}\),同一组内的物品最多只能选一个。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大,输出最大价值。\(0<n,m\le 100,0<s_i,v_{i,j},w_{i,j}\le 100\)。
思路:由于每一组内的物品最多只能选一个,我们可以对每一组都做一次 01 背包。时间复杂度 \(O(nm\sum s_i)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N], f[N];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) {
int s; scanf("%d", &s);
for (int i = 1; i <= s; ++i) scanf("%d%d", &v[i], &w[i]);
for (int j = m; j >= 0; --j) { // 注意,由于每一组最多选一个,我们先枚举体积
for (int k = 1; k <= s; ++k)
if (j >= v[k])
f[j] = max(f[j], f[j-v[k]]+w[k]);
}
}
printf("%d\n", f[m]);
return 0;
}
5.2 线性 DP
题目:给定一个 \(n\) 层的数字三角形 \(a\),从顶部出发,在每一节点可以选择移动至其左下方的节点或右下方的节点,一直走到底层。计算出路径上的数之和的最大值。\(1\le n\le 500,-10000\le a_{i,j}\le 10000\)。
下面展示了一个 \(5\) 层的数字三角形:
8
2 3
1 6 7
2 3 4 2
1 1 4 5 1
思路:
从上往下不好考虑,我们不妨从下往上想。
定义 \(f_{i,j}\) 表示从下往上走到第 \(i\) 行第 \(j\) 个数的路径上的数之和最大值。初始状态 \(f_{n,j}=a_{n,j}\),目标状态为 \(f_{1,1}\)。
考虑状态转移:
- 移动至左下方:路径上的数之和为 \(f_{i+1,j}+a_{i,j}\);
- 移动至右下方:路径上的数之和为 \(f_{i+1,j+1}+a_{i,j}\)。
则状态转移方程为:
时间复杂度 \(O(n^2)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 510;
int n;
int a[N][N], f[N][N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= i; ++j)
scanf("%d", &a[i][j]);
}
for (int j = 1; j <= n; ++j) f[n][j] = a[n][j];
for (int i = n-1; i >= 1; --i) {
for (int j = 1; j <= i; ++j)
f[i][j] = a[i][j] + max(f[i+1][j], f[i+1][j+1]);
}
printf("%d\n", f[1][1]);
return 0;
}
题目:给定一个长度为 \(n\) 的序列 \(a\),求数值严格单调递增的子序列的长度最长是多少。\(1\le n\le 1000,-10^9\le a_i\le 10^9\)。
思路:
定义 \(f_i\) 表示以第 \(i\) 个数为结尾的最长上升子序列长度。初始状态 \(f_i=1\),答案为 \(\max_{i=1}^n f_i\)。
考虑状态转移:若 \(a_j<a_i\;(j<i)\),则以第 \(i\) 个数为结尾的上升子序列可以是以第 \(j\) 个数为结尾的最长上升子序列再加上第 \(i\) 个数,此时以 \(i\) 为结尾的最长上升子序列的长度为 \(f_j+1\)。所以状态转移方程为:
时间复杂度 \(O(n^2)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, ans = 1;
int a[N], f[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
f[1] = 1;
for (int i = 2; i <= n; ++i) {
f[i] = 1;
for (int j = 1; j < i; ++j) {
if (a[i] > a[j])
f[i] = max(f[i], f[j]+1);
}
ans = max(ans, f[i]);
}
printf("%d\n", ans);
return 0;
}
题目:给定一个长度为 \(n\) 的序列 \(a\),求数值严格单调递增的子序列的长度最长是多少。\(1\le n\le 10^5,-10^9\le a_i\le 10^9\)。
思路:
令 \(f_{i}\) 表示对于所有长度为 \(i\) 的单调上升子序列,其最后一项的大小的最小值。特别地,若不存在则 \(f_i=0\)。
接下来我们来证明:随 \(i\) 增大,\(f_i\) 单调不减。即 \(f_i\le f_{i+1}\)。
考虑使用反证法。设存在 \(u<v\) 使得 \(f_u>f_v\)。考虑长度为 \(v\) 的上升子序列,根据定义它以 \(f_v\) 结尾。显然我们可以从该序列中挑选出一个长度为 \(u\) 的上升子序列,它的结尾同样是 \(f_v\)。由于 \(f_u>f_v\),与 \(f_u\) 最小相矛盾。
因此 \(f_i\) 是单调不增的。
考虑以 \(i\) 结尾的单调递增子序列的长度的最大值 \(dp_i\)。由于我们需要计算所有满足 \(a_j<a_i\) 的 \(j\) 中,\(dp_j\) 的最大值,设 \(dp_j=x\),若 \(a_i<f_x\),又因为 \(f_x\le a_j\),就有 \(a_i<a_j\),矛盾。因此总有 \(a_i\ge f_x\)。又因为 \(f_i\) 单调不减,我们可以通过二分找到最小的 \(x\) 满足 \(a_i\ge f_x\)。
时间复杂度 \(O(n\log n)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 1e5+10;
int n;
int a[N];
vector<int> s;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i <= n; ++i) {
int pos = lower_bound(s.begin(), s.end(), a[i]) - s.begin();
if (pos == s.size()) s.push_back(a[i]);
else s[pos] = a[i];
}
printf("%d\n", s.size());
return 0;
}
题目:给定两个长度分别为 \(n,m\) 的字符串 \(A,B\),求出它们的最长公共子序列长度。\(1\le n,m\le 1000\),\(A,B\) 由小写字母构成。
题目:
定义 \(f_{i,j}\) 表示考虑到 \(A\) 中前 \(i\) 个字符,\(B\) 中前 \(j\) 个字符的最长公共子序列长度。初始状态为 \(f_{0,0}=0\),答案为 \(f_{n,m}\)。
考虑状态转移:
- \(a_i,b_j\) 都不选:\(f_{i,j}=f_{i-1,j-1}\);
- \(a_i,b_j\) 都选(\(a_i=b_j\)):\(f_{i,j}=f_{i-1,j-1}+1\);
- 选 \(a_i\),不选 \(b_j\):第一眼看起来,答案似乎是 \(f_{i,j-1}\),但 \(f_{i,j-1}\) 尽管满足了不包含 \(b_j\) 的要求,但却不能保证 \(a_i\) 在公共子序列中。可以证明,不存在一种状态能够准确无误地表示出这种情况。
注意到,第 3 种情况实际上是包含在 \(f_{i,j-1}\) 之中,但其中还包含了第 1 种情况。由于 \(\max\) 运算只要求不漏,并没有要求不重,所以 我们其实可以将第 3 种情况视作 \(f_{i.j-1}\),对答案并没有影响。
- 不选 \(a_i\),选 \(b_j\):同第 3 种情况,我们可以将其视作 \(f_{i-1,j}\)。
所以想要求出 \(f_{i,j}\),只需要求出第 2,3,4 种情况的最大值即可。
状态转移方程为:
时间复杂度 \(O(nm)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
char A[N], B[N];
int f[N][N];
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
cin >> A+1 >> B+1;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
f[i][j] = max(f[i-1][j], f[i][j-1]);
if (A[i] == B[j]) f[i][j] = max(f[i][j], f[i-1][j-1]+1);
}
}
cout << f[n][m] << endl;
return 0;
}
题目:给定两个长度分别为 \(n,m\) 的字符串 \(A,B\),现在要将 \(A\) 经过若干操作变为 \(B\),可进行的操作有:
- 删除:将 \(A\) 中的某个字符删除;
- 插入:在 \(A\) 的某个位置插入一个字符;
- 修改:将 \(A\) 中的某个字符修改为另一个字符。
求出将 \(A\) 变为 \(B\) 至少需要多少次操作(最短编辑距离)。\(1\le n,m\le 1000\),\(A,B\) 中只包含大写字母。
思路:
定义 \(f_{i,j}\) 表示将 \(A\) 中前 \(i\) 个字符修改为 \(B\) 中前 \(j\) 个字符的最短编辑距离。
先来讨论初始化:对于 \(f_{0,i}\;(0\le i\le m)\),其表示 \(A\) 中前 \(0\) 个字符变为 \(B\) 中前 \(i\) 个字符的最短编辑距离,显然每一次操作都是插入操作,所以 \(f_{0,i}=i\);对于 \(f_{i,0}\;(0\le i\le n)\),其表示 \(A\) 中前 \(i\) 个字符变为 \(B\) 中前 \(0\) 个字符的最短编辑距离,显然每一次操作都是删除操作,所以 \(f_{i,0}=i\)。
接下来考虑状态转移:
- 不操作(\(A_i=B_j\)):\(f_{i,j}=f_{i-1,j-1}\);
- 删除操作:删除 \(A_i\) 后,\(A\) 中前 \((i-1)\) 个字符与 \(B\) 中前 \(j\) 个字符相等,所以 \(f_{i,j}=f_{i-1,j}+1\);
- 插入操作:在\(A\) 中第 \(i\) 个字符后插入一个字符,使得 \(A_{i+1}=B_j\),可以视作 \(A\) 中前 \(i\) 个字符与 \(B\) 中前 \((j-1)\) 个字符相等,所以 \(f_{i,j}=f_{i,j-1}+1\)。
- 修改操作:将 \(A_i\) 修改为 \(B_j\),使得 \(A\) 中前 \(i\) 个字符与 \(B\) 中前 \(j\) 个字符相等,可以视作 \(A\) 中前 \((i-1)\) 个字符与 \(B\) 中前 \((j-1)\) 个字符相等,所以 \(f_{i,j}=f_{i-1,j-1}+1\)。
所以当 \(A_i=B_j\) 时,状态转移方程为:
当 \(A_i\ne B_j\) 时,状态转移方程为:
目标状态为 \(f_{n,m}\)。
时间复杂度 \(O(nm)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
char A[N], B[N];
int f[N][N];
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> A+1 >> m >> B+1;
for (int i = 0; i <= max(n, m); ++i) f[0][i] = f[i][0] = i;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
if (A[i] == B[j]) f[i][j] = min(f[i-1][j-1], min(f[i][j-1]+1, f[i-1][j]+1));
else f[i][j] = min(f[i-1][j-1], min(f[i][j-1], f[i-1][j])) + 1;
}
}
printf("%d\n", f[n][m]);
return 0;
}
题目:给定 \(n\) 个字符串 \(a_1\sim a_n\) 和 \(m\) 次询问,每次询问给出一个字符串 \(s\) 和一个操作上限 \(k\)。对于每次询问,求出 \(n\) 个字符串中有多少个字符串可以在 \(k\) 次操作(删除、插入、修改)内变为 \(s\)。\(1\le n,m\le 1000,1\le |a_i|,|s|\le 10\),字符串内只包含小写字母。
思路:直接按 AcWing 902. 最短编辑距离 中的转移方程计算即可。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010, M = 15;
int n, m, k, cnt;
int f[M][M];
char str[N][M], s[M];
int edit_distance(char A[], char B[]) {
int s1 = strlen(A+1), s2 = strlen(B+1);
for (int i = 0; i <= max(s1, s2); ++i) f[i][0] = f[0][i] = i;
for (int i = 1; i <= s1; ++i) {
for (int j = 1; j <= s2; ++j) {
if (A[i] == B[j]) f[i][j] = min(f[i-1][j-1], min(f[i-1][j]+1, f[i][j-1]+1));
else f[i][j] = min(f[i-1][j-1], min(f[i-1][j], f[i][j-1])) + 1;
}
}
return f[s1][s2];
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> str[i]+1;
while (m -- ) {
cnt = 0;
cin >> s+1 >> k;
for (int i = 1; i <= n; ++i) {
if (edit_distance(str[i], s) <= k)
cnt ++;
}
cout << cnt << '\n';
}
return 0;
}
5.3 区间 DP
题目:有编号为 \(1\sim n\) 的 \(n\) 堆石子,第 \(i\) 堆石子的质量为 \(a_i\)。现在要将这 \(n\) 堆石子合为一堆,合并相邻两堆的代价是这两堆的石子质量之和,合并前与这两堆石子相邻的石子会与新的堆相邻,求出合并的最小总代价。\(1\le n\le 300,1\le a_i\le 1000\)。
思路:
定义 \(f_{i,j}\) 表示合并区间 \([i,j]\) 中的石子的最小总代价。初始状态为 \(f_{i,i}=0\),目标状态为 \(f_{1,n}\)。
考虑状态转移(\(i<j\)):由于最终的石子堆一定是由相邻的两堆 \([i,k]\) 和 \([k+1,j]\) 合并而来的,所以合并成这两堆需要的代价为 \(f_{i,k}+f_{k+1,j}\)。另外还需要加上这两堆中的石子质量,显然是 \(\sum_{t=i}^k a_t+\sum_{t=k+1}^j a_t=\sum_{t=i}^j a_i\)。这个石子可以用前缀和优化,令 \(s_i=\sum_{t=1}^i a_t\),则两堆的石子质量之和为 \(s_j-s_{i-1}\)。
状态转移方程为:
在区间 DP 中,我们通常先枚举区间长度 \(len\),再枚举区间左端点 \(i\),则此时区间右端点 \(j=i+len-1\)。
时间复杂度 \(O(n^3)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 310;
int n;
int a[N], s[N];
int f[N][N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]), s[i] = s[i-1] + a[i];
memset(f, 0x3f, sizeof f);
for (int i = 1; i <= n; ++i) f[i][i] = 0;
for (int len = 1; len <= n; ++len) {
for (int i = 1; i <= n-len+1; ++i) {
int j = i + len - 1;
for (int k = i; k <= j; ++k)
f[i][j] = min(f[i][j], f[i][k]+f[k+1][j]+s[j]-s[i-1]);
}
}
printf("%d\n", f[1][n]);
return 0;
}
5.4 计数 DP
题目:一个正整数可以被表示为若干个正整数之和,形如 \(n=\sum_{i=1}^k n_i\),其中 \(n_k\le n_{k-1}\le\cdots\le n_1,k\ge 1\)。我们将这样的一种表示称为正整数 \(n\) 的一种划分。给定一个正整数 \(n\),计算 \(n\) 的划分数量对 \(10^9+7\) 取模后的结果。\(1\le n\le 1000\)。
思路:
我们将 \(1,2,\cdots,n\) 看作体积不同的各个物体,每个物体均有无限个。这样求 \(n\) 的划分数量就可以转换为完全背包问题进行计算。
定义 \(f_{i,j}\) 表示考虑前 \(i\) 个整数,能够拼成整数 \(j\) 的方案数。初始状态为 \(f_{0,j}=f_{i,0}=1\)(都不选也是一种方案),目标状态为 \(f_{n,n}\)。
考虑状态转移:
- 不选第 \(i\) 个整数:方案数为 \(f_{i-1,j}\);
- 选 \(k\) 个第 \(i\) 个整数(\(k>0\)):方案数为 \(f_{i-1,j-ki}\)。
与完全背包问题类似,第 2 种状态的方案数为 \(f_{i,j-i}\)。所以状态转移方程即为:
注意到第一维可以优化掉,时间复杂度 \(O(n^2)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1010, mod = 1e9+7;
int n;
int f[N];
int main() {
scanf("%d", &n);
f[0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = i; j <= n; ++j)
f[j] = (f[j]+f[j-i]) % mod;
}
printf("%d\n", f[n]);
return 0;
}
5.5 数位 DP
题目:给定多组测试数据,每组数据包含两个整数 \(a,b\),计算 \([a,b]\) 中所有整数中 \(0\sim 9\) 的出现次数。\(0< a,b< 10^8\)。
思路:
首先有一个想法:\([a,b]\) 中数字 \(i\) 出现的次数,等于 \([1,b]\) 中数字 \(i\) 出现的次数减去 \([1,a-1]\) 中数字 \(i\) 出现的次数。现在问题转化为求 \([1,b]\) 中数字 \(i\) 出现的个数。
假设当前考虑到 \(b\) 从右往左数第 \(j\) 位,令 \(l=n/10^j\)(即 \(l\) 是 \(b\) 中在第 \(j\) 位左边的部分),\(r=n\bmod 10^{j-1}\)(即 \(r\) 是 \(b\) 中在第 \(j\) 位右边的部分)。我们分情况讨论:
- 新数第 \(j\) 位左边的部分小于 \(l\):
- \(i\ne 0\):此时第 \(j\) 位右边的部分可以随便取,数量为 \(l\times 10^{j-1}\);
- \(i=0\) 且 \(l\ne 0\):此时第 \(j\) 位右边的部分不能全为 \(0\),数量为 \((l-1)\times 10^{j-1}\)。
- 新数第 \(j\) 位左边恰好等于 \(l\)(\(l\ne 0\) 或 \(i\ne 0\)):
- \(b\) 中第 \(j\) 位的数小于 \(i\):数量为 \(0\);
- \(b\) 中第 \(j\) 位的数恰好为 \(i\):数量为 \(r+1\);
- \(b\) 中第 \(j\) 位的数大于 \(i\):后面的部分可以随便取,数量为 \(10^{j-1}\)。
由此计算即可。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
int a, b;
int get_digit(int n) {
int s = 0;
while (n) n /= 10, s ++;
return s;
}
int count(int n, int i) {
int cnt = 0, d = get_digit(n);
for (int j = 1; j <= d; ++j) {
int p = pow(10, j-1), l = n / (p*10), r = n % p;
// 第j位左边小于l
if (i) cnt += l * p;
else if (l) cnt += (l-1) * p;
// 第j位左边等于l
int t = n / p % 10;
if (t == i && (i || l)) cnt += r+1;
else if (t > i && (i || l)) cnt += p;
}
return cnt;
}
int main() {
while (cin >> a >> b, a || b) {
if (a > b) swap(a, b);
for (int i = 0; i <= 9; ++i)
printf("%d ", count(b, i)-count(a-1, i));
puts("");
}
return 0;
}
5.6 状压 DP
题目:给定多组测试数据,每组数据给定两个整数 \(n,m\),计算用 \(1\times 2\) 的小长方形铺满 \(n\times m\) 的大长方形方式数量。\(1\le n,m\le 11\)。
思路:
这道题有一个突破口:由于竖着放的小长方形的位置是由横着放的小长方形决定的,所以横着放的小长方形的合法方案数即为答案。思考怎样的状态为合法状态:摆好所有横着的小长方形后,每一列连续空着的位置必须为偶数。
定义 \(f_{i,j}\) 表示前 \((i-1)\) 列已经摆好,当前为第 \(i\) 列,这一列的状态为 \(j\) 的方案数。对于编号为 \(j\) 的状态,我们用一个 \(n\) 位二进制整数表示小长方形的放置情况,其二进制表示的第 \(k\;(1\le k\le n)\) 位为 \(1\) 时,表示第 \((i-1)\) 列第 \(k\) 行伸出了一个横着的小长方形到第 \(i\) 行。那么初始状态为 \(f_{1,0}\)(因为第 \(0\) 列必定为空,所以伸到第 \(1\) 列的状态必然为 \(0\),即没有伸出来的小长方形),目标状态为 \(f_{m+1,0}\)(因为前 \(m\) 列都要摆好,且第 \(m\) 列的小长方形不能伸到大长方形外面,所以伸到第 \((m+1)\) 列的状态为 \(0\))。
接下来我们来考虑状态转移。我们考虑 \(f_{i-1,k}\) 如何转移至 \(f_{i,j}\),其表示从第 \((i-2)\) 列伸出到第 \((i-1)\) 列的状态为 \(k\) 的数量。由于 \((i-2)\) 列的小长方形若伸到第 \((i-1)\) 列,则其必然不能伸到第 \(i\) 列,否则会产生重叠,如下图:
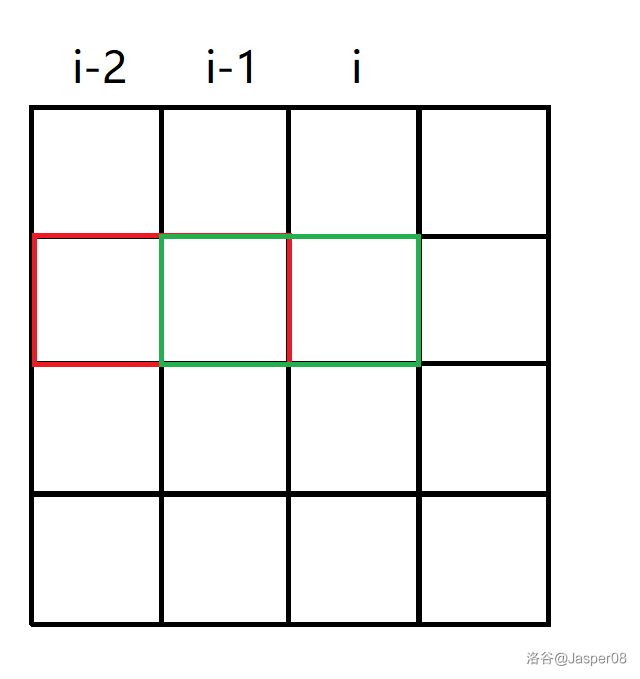
红色的小长方形和绿色的小长方形重叠了,这种状态不可能存在。所以当 \(j\;\&k\;=0\)(其中 \(\&\) 表示按位与)时,\(f_{i-1,k}\) 才能转移到 \(f_{i,j}\)。
状态转移方程是显而易见的:
其中 \(j,k\) 均为合法状态。
时间复杂度 \(O(m2^n)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
#define int long long
const int N = 13;
int n, m;
int f[N][1<<N];
bool st[1<<N]; // 存储每一个状态是否合法
vector<int> state[1<<N]; // 存储每一个状态可以由哪些状态转移而来
signed main() {
while (cin >> n >> m, n || m) {
// 预处理 st 数组
for (int s = 0; s < (1 << n); ++s) {
int cnt = 0; bool check = 1;
for (int j = 1; j <= n; ++j) {
if ((s >> j-1) & 1) {
if (cnt & 1) {check = 0; break;}
else cnt = 0;
}
else cnt ++;
}
if (cnt & 1) check = 0;
st[s] = check;
}
// 预处理 state 数组
for (int s = 0; s < (1 << n); ++s) {
state[s].clear();
for (int ss = 0; ss < (1 << n); ++ss) {
if (!(s & ss) && st[s|ss])
state[s].push_back(ss);
}
}
// 初始化
memset(f, 0, sizeof f);
f[1][0] = 1;
// dp
for (int i = 2; i <= m+1; ++i) {
for (int j = 0; j < (1 << n); ++j) {
for (auto k : state[j])
f[i][j] += f[i-1][k];
}
}
cout << f[m+1][0] << endl;
}
return 0;
}
题目:给定一张 \(n\) 个点的带权无向图,图中的点从 \(0\sim n-1\) 标号。求起点 \(0\) 到终点 \(n-1\) 的最短 Hamilton 路径。记 \(d(i,j)\) 表示 \(i\) 到 \(j\) 的距离,保证 \(d(i,i)=0,d(i,j)=d(j,i),d(i,j)+d(j,k)\ge d(i,k)\)。\(1\le n\le 20,1\le d(i,j)\le 10^7\)。
Hamilton 路径:从 \(0\) 到 \(n-1\) 的所有点都不重不漏地经过一次的路径。
思路:
注意到我们在计算从 \(0\rightarrow i\) 的最短路径时,其实并不关心经过了哪些点,而只关心走过的路径的最小值。因此我们可以用状压 DP 来解决这个问题。
定义 \(f_{i,j}\) 表示走到第 \(i\) 号点,经过的点集为 \(j\) 的最短路径,那么初始状态为 \(f_{0,1}=0\),目标状态为 \(f_{n-1,2^n-1}\)。
考虑状态转移:假设要从 \(k\) 号点走到 \(i\) 号点,那么根据 Hamilton 路径的定义,走到 \(k\) 的路径必然不能经过 \(i\)。那么状态转移方程为:
时间复杂度 \(O(n^22^n)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 20;
int n;
int g[N][N];
int f[N][1<<N];
int main() {
scanf("%d", &n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j)
scanf("%d", &g[i][j]);
}
memset(f, 0x3f, sizeof f);
f[0][1] = 0;
for (int s = 1; s < (1 << n); ++s) {
if (!(s & 1)) continue;
for (int i = 0; i < n; ++i) {
if (!(s >> i & 1)) continue;
for (int j = 0; j < n; ++j)
if ((s ^ (1<<i)) >> j & 1)
f[i][s] = min(f[i][s], f[j][s^(1<<i)]+g[j][i]);
}
}
printf("%d\n", f[n-1][(1<<n)-1]);
return 0;
}
5.7 树形 DP
题目:Ural 大学中有 \(n\) 个职员,编号为 \(1\sim n\)。除了校长之外,所有人都有一位直接上司。第 \(i\) 个职员都有一个快乐程度 \(h_i\),现在要举办一场宴会,每个职员不能和自己的直接上司一起参会,求出可以得到的最大快乐程度之和。\(1\le n\le 6000,-128\le h_i\le 127\)。
思路:
我们可以将职员之间的关系视作一棵树,每个人的直接上司和他之间有一条有向边,显然校长为根节点。
定义 \(f_{i,0/1}\) 表示以 \(i\) 为根节点的子树,选/不选 \(i\) 号节点的最大价值。对于所有的叶子结点,有 \(f_{i,0}=0,f_{i,1}=h_i\)。答案为 \(\max(f_{root,0},f_{root,1})\)。
考虑状态转移:
- \(f_{i,0}\):不选 \(i\) 号节点,那么其儿子节点就可以选,也可以不选。所以有 \(f_{i,0}=\sum_{(i,j)\in E} \max(f_{j,1},f_{j,0})\);
- \(f_{i,1}\):选 \(i\) 号节点,那么其儿子节点就必然不能选。所以有 \(f_{i,1}=\sum_{(i,j)\in E} f_{j,0}\)。
综上,状态转移方程为:
树形 DP 可以用建图和 DFS 实现,时间复杂度 \(O(n)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 6010;
int n, root;
int h[N], e[N], ne[N], idx;
int H[N], f[N][2];
bool R[N];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u) {
f[u][1] = H[u];
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
dfs(j);
f[u][1] += f[j][0], f[u][0] += max(f[j][0], f[j][1]);
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &H[i]);
memset(h, -1, sizeof h);
for (int i = 1; i < n; ++i) {
int l, k; scanf("%d%d", &l, &k);
add(k, l), R[l] = 1;
}
for (int i = 1; i <= n; ++i) {
if (!R[i]) {root = i; break;}
}
dfs(root);
printf("%d\n", max(f[root][0], f[root][1]));
return 0;
}
5.8 记忆化搜索
题目:有一个 \(r\) 行 \(c\) 列的滑雪场,每个点 \((i,j)\) 都有一个高度 \(h_{i,j}\)。一个人从滑雪场的任意一点出发,每一次可以沿从点 \((x,y)\) 上下左右任意一个方向移动一个单位到达点 \((x',y')\),满足 \(h_{x,y}>h_{x',y'}\)。计算出这个人所能滑动的最长距离。\(1\le r,c\le 300,1\le h_{i,j}\le 10000\)。
思路:
我们可以使用记忆化搜索,即每次搜索完一个格子后存下这个格子所能滑动的最长距离 \(f_{i,j}\),下次再搜到这个点时,直接将距离加上 \(f_{i,j}\) 即可,不用再进行重复搜索。
需要注意,由于我们到达点 \((x,y)\) 时,\(h_{x,y}\) 一定小于我们前面经过的所有点的高度,所以不会产生重复的路线。
时间复杂度 \(O(n^2)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 310;
const int dx[] = {-1, 0, 1, 0}, dy[] = {0, -1, 0, 1};
int r, c, ans;
int f[N][N], h[N][N];
int dfs(int x, int y) {
if (f[x][y]) return f[x][y]; // 记忆化
f[x][y] = 1;
for (int i = 0; i < 4; ++i) {
int x_ = x + dx[i], y_ = y + dy[i];
if (x_ > 0 && x_ <= r && y_ > 0 && y_ <= c && h[x][y] > h[x_][y_])
f[x][y] = max(f[x][y], 1+dfs(x_, y_));
}
return f[x][y];
}
int main() {
scanf("%d%d", &r, &c);
for (int i = 1; i <= r; ++i) {
for (int j = 1; j <= c; ++j)
scanf("%d", &h[i][j]);
}
for (int i = 1; i <= r; ++i) {
for (int j = 1; j <= c; ++j)
ans = max(ans, dfs(i, j));
}
printf("%d\n", ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号