DirectedGraph

有向图

有向图就是边是有方向的图，例如：

 

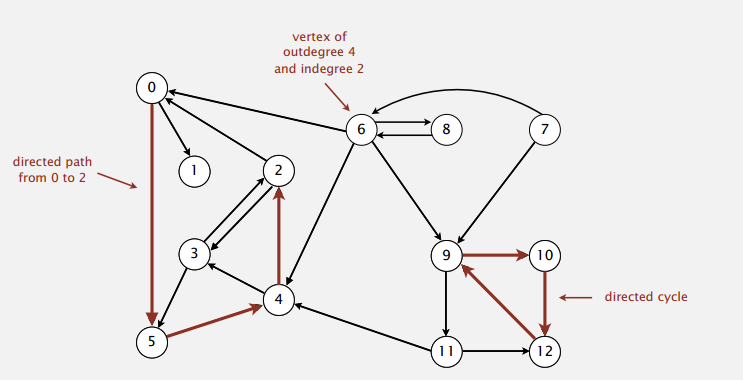
Digraph API

 

java implementation 只是修改了 addEdge方法 addEdge(v,w) 增加了一条从v指向w 的边

public class Digraph {
    private final int V;
    private int E;
    private Bag<Integer>[] adj;
    public Digraph(int V){
        this.V = V;
        this.E = 0;
        adj = (Bag<Integer>[]) new Bag[V];
        for (int i = 0; i < V; i++) {
            adj[i] = new Bag<Integer>();
        }
    }
    public int V(){
        return V;
    }
    public int E(){
        return E;
    }
    public void addEdge(int v , int w){
        adj[v].add(w);
        E++;
    }
    public Iterable<Integer> adj(int v){
        return adj[v];
    }
    public Digraph reverse(){
        Digraph R = new Digraph(V);
        for (int i = 0; i < V; i++) {
            for (Integer w : adj[i]) {
                R.addEdge(w,i);
            }
        }
        return R;
    }

    public static void main(String[] args) {

    }
}

对于Digraph 的搜索仍然可以用 dfs 和 bfs 。、

拓扑排序

 

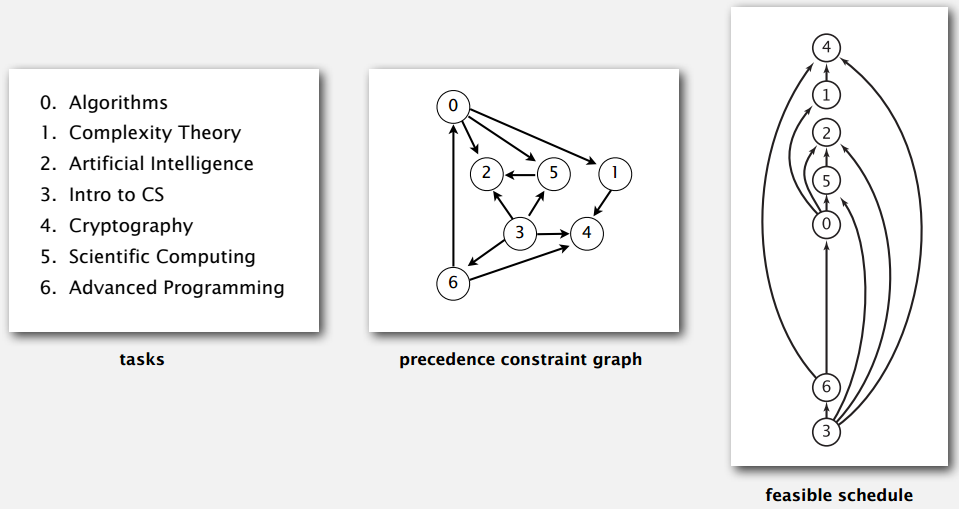
拓扑排序就是将有向图的排列方式改为箭头只朝一个方向的形式，比如大学里面前置课程的排列。拓扑排序适用于无环图（DAG, directed acyclic graph）

只需要把dfs做一点改动就可以实现拓扑排序。

先来看三种访问的顺序：

• 前序（Preorder）：在递归调用之前将点加入队列。
• 后序（Postorder）：在递归调用之后将点加入队列。
• 逆后序（Reverse postorder）：在递归调用之后将点压入栈。

三种访问方式的java implementation

public class DepthFirstOrder {
    private boolean[] marked;
    private Queue<Integer> pre;
    private Queue<Integer> post;
    private Stack<Integer> reversePost;
    public DepthFirstOrder(Digraph G){
        marked = new boolean[G.V()];
        pre = new Queue<>();
        post = new Queue<>();
        reversePost = new Stack<>();
        for (int i = 0; i < G.V(); i++) {
            if (!marked[i]){
                dfs(G, i);
            }
        }
    }
    private void dfs(Digraph G , int v){
        pre.enqueue(v);
        marked[v] = true;
        for (Integer w : G.adj(v)) {
            if (!marked[w]){
                dfs(G,w);
            }
        }
        post.enqueue(v);
        reversePost.push(v);
    }
    public Iterable<Integer> pre(){
        return pre;
    }
    public Iterable<Integer> post(){
        return post;
    }
    public Iterable<Integer> reversePost(){
        return reversePost;
    }
}

Directed Cycle Detetion

拓扑排序的重要环节就是判断有向图是不是DAG,这时候只用维护一个OnStack的boolean数组就可以判断这条路径上曾经有没有访问过这个元素。

在进行dfs之后要把Onstack 的元素值恢复成默认值。以便下一个component 判断 Directed Cycle

public class DirectedCycle {
    private boolean[] marked;
    private int[] edgeTo;
    private Stack<Integer> cycle;
    private boolean[] onStack;
    public DirectedCycle(Digraph G){
        marked = new boolean[G.V()];
        edgeTo = new int[G.V()];
        onStack = new boolean[G.V()];
        for (int i = 0; i < G.V(); i++) {
            if (!marked[i]){
                dfs(G,i);
            }
        }
    }
    private void dfs(Digraph G , int v ){
        onStack[v] = true;
        marked[v] = true;
        for (Integer w : G.adj(v)) {
            if (hasCycle()){
                return;
            }else if (!marked[w]){
                edgeTo[w] = v;
                dfs(G,w);
            }else if (onStack[w]){
                cycle = new Stack<Integer>();
                for (int i = v; i !=v;i = edgeTo[i]){
                    cycle.push(i);
                }
                cycle.push(w);
                cycle.push(v);
            }
        }
        onStack[v] = false;
    }
    public boolean hasCycle(){
        return cycle !=null;
    }
    public Iterable<Integer> cycle(){
        return cycle;
    }
}

Strong Components

强连通。在有向图中，若同时存在路径 v->w 和 w->v，则称点 v 和 w 是强连通的。类似的，这显然也是一个等价关系，满足：

1. symmetric: 自反性， v 和 v 自身是强连通的。
2. reflexive: 对称性， v 和 w 强连通，则 w 和 v 强连通。
3. transitive: 传递性，如果 v 和 w 强连通，又有 w 和 x 强连通，那么 v 和 x 强连通。

强连通分量也很好理解，就是区域里面的点之间都是强连通的。

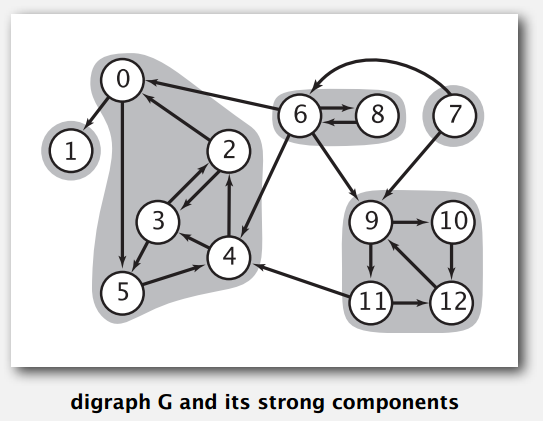
计算强连通分量的算法叫kosaraju-sharir 算法

主要思想是算核心 DAG （把强连通分量当成一个点）的拓扑排序，再按逆拓扑序列对点跑 DFS。

主要有两个步骤：

Step 1 ： 先用DepthFirstOrder得到 Graph的反转图的逆后序序列。

Step 2：再用这个逆后序序列对 Graph 进行 dfs 操作;

public class KosarajuSCC {
    private boolean[] marked;
    private int count;
    private int[] id;
    public KosarajuSCC(Digraph G){
        marked = new boolean[G.V()];
        id = new int[G.V()];
        DepthFirstOrder order = new DepthFirstOrder(G.reverse());
        for (Integer s : order.reversePost()) {
            if (!marked[s]){
                dfs(G,s);
                count++;
            }
        }
    }
    private void dfs(Digraph G , int v){
        marked[v] = true;
        id[v] = count;
        for (Integer w : G.adj(v)) {
            if (!marked[w]){
                dfs(G,w);
            }
        }
    }
    public boolean stronglyConnected(int v , int w){
        return id[v] == id[w];
    }
    public int id(int w){
        return id[w];
    }
    public int count(){
        return count;
    }
}