C++-蓝桥杯-斐波拉契[2014真题][数学推导][数论][矩阵快速幂][大数取模][快速防爆乘]
首先一秒钟想到的斐波拉契模板,矩阵快速幂加速
之前有过类似博客,这里不赘述原理。
1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 using namespace std; 5 typedef long long ll; 6 struct Matrix{ 7 ll a[3][3]; 8 }; 9 Matrix P(int type){ 10 Matrix A; 11 for(int i=1;i<=2;i++)for(int j=1;j<=2;j++)A.a[i][j]=type?(i==j):0; 12 return A; 13 } 14 Matrix Mul(Matrix A,Matrix B,ll MOD){ 15 Matrix C=P(0); 16 for(int i=1;i<=2;i++) 17 for(int j=1;j<=2;j++) 18 for(int k=1;k<=2;k++) 19 C.a[i][j]=(C.a[i][j]+A.a[i][k]*B.a[k][j])%MOD; 20 return C; 21 } 22 Matrix Pow(Matrix A,ll b,ll MOD){ 23 Matrix B=P(1); 24 for(;b;b>>=1,A=Mul(A,A,MOD))if(b&1)B=Mul(B,A,MOD); 25 return B; 26 } 27 ll F(ll n,ll MOD){ 28 Matrix A; 29 A.a[1][1]=1,A.a[1][2]=1; 30 A.a[2][1]=1,A.a[2][2]=0; 31 Matrix B=P(0); 32 B.a[1][2]=1; 33 B=Mul(B,Pow(A,n,MOD),MOD); 34 return B.a[1][1]; 35 } 36 int main(){ 37 for(int i=1;i<=30;i++)cout<<F(i,1e9)<<endl; 38 return 0; 39 }
然后是一辈子想不到的,数学推导
来源=>这是个巨佬https://blog.csdn.net/acdreamers/article/details/21822165
第一步:

第二步:
引用一:
![]()
证明,数学归纳法,过程略,这个比较简单
引用二:
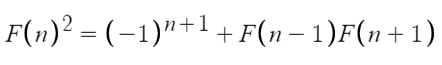
证明(依然是数学归纳法,但是要点技巧):
上式等价于:

当n=1,2时,等式显然成立(F[0]=0)
假设n=k成立,则有:
![]()

![]()
证毕。
引用三:
![]()
这个证明,博主表示不会
对上式换元,令
![]()
则有:
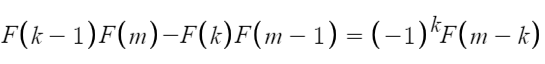
经过恒等变形:

第三步:
考虑:
![]()
![]()
![]()
对于F(n-m)递归下去,可以得到:
![]()
这里直接令k=n%m
第四步:
由引用二可得:
![]()
![]()
然后对于m,n/m,n/(2m),n%m的奇偶性,展开分类讨论
设a=n/m,b=n/(2m),k=n%m
①当m为奇数时:
![]()
1.a为偶数b为偶数 F(n)modF(m) = F(n%m) =F(k)
2.a为偶数b为奇数 F(n)modF(m) = [-F(n%m)]modF(m) = F(m)-F(k)
3.a为奇数b为偶数 F(n)modF(m) = F(m-1)F(n%m)modF(m) = F(m-1)F(k)modF(m)
4.a为奇数b为奇数 F(n)modF(m) = [-F(m-1)F(n%m)]modF(m) =F(m)-F(m-1)F(k)modF(m)
②当m为偶数时:
![]()
1.a为偶数 F(n)modF(m) = F(n%m) = F(k)
2.a为奇数 F(n)modF(m) = F(m-1)F(n%m)modF(m) = F(m-1)F(k)modF(m)
对于橙色部分:
有引用三,k=n%m,所以有
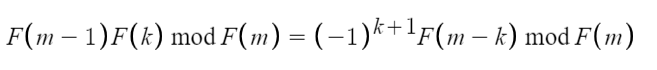
![]()
化简到此时,我们可以注意到,斐波拉契数的下标都已经小于了m,也就是说对于%F(m)操作,我们可以忽略了
1.当k为奇数时:F(m-1)F(k)modF(m) = F(m-k)
2.当k为偶数时:F(m-1)F(k)modF(m) = F(m)-F(m-k)
于是我们得到了一个满分算法
第五步:
虽然是满分算法,但是如果不注意细节可能就60分,倒大霉了!
在进行ll类型的乘法时,由于模数是接近ll极限的,所以我们需要写快速防爆乘,思路和快速幂类似,也是倍增写法
第六步:
上代码,A掉它!!!
PS:由于蓝桥杯数据太少,虽然可以做到0msAC,但是不能保证代码完全正确,可能有小错误,毕竟分类讨论这么多,比测试数据还多
1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 using namespace std; 5 typedef long long ll; 6 struct Matrix{ll a[3][3];}; 7 ll Mul(ll a,ll b,ll MOD){ 8 ll ans=0; 9 for(;b;b>>=1,a=(a+a)%MOD)if(b&1)ans=(ans+a)%MOD; 10 return ans; 11 } 12 Matrix P(int type){ 13 Matrix A; 14 for(int i=1;i<=2;i++)for(int j=1;j<=2;j++)A.a[i][j]=type?(i==j):0; 15 return A; 16 } 17 Matrix Mul(Matrix A,Matrix B,ll MOD){ 18 Matrix C=P(0); 19 for(int i=1;i<=2;i++) 20 for(int j=1;j<=2;j++) 21 for(int k=1;k<=2;k++) 22 C.a[i][j]=(C.a[i][j]+Mul(A.a[i][k],B.a[k][j],MOD))%MOD; 23 return C; 24 } 25 Matrix Pow(Matrix A,ll b,ll MOD){ 26 Matrix B=P(1); 27 for(;b;b>>=1,A=Mul(A,A,MOD))if(b&1)B=Mul(B,A,MOD); 28 return B; 29 } 30 ll F(ll n,ll MOD){ 31 Matrix A; 32 A.a[1][1]=1,A.a[1][2]=1; 33 A.a[2][1]=1,A.a[2][2]=0; 34 Matrix B=P(0); 35 B.a[1][2]=1; 36 B=Mul(B,Pow(A,n,MOD),MOD); 37 return B.a[1][1]; 38 } 39 ll calc(ll n,ll m,ll MOD){ 40 ll a=n/m,b=n/(2*m),k=n%m; 41 if(m&1){ 42 if((a&1)&&(b&1)){ 43 if(k&1)return (F(m,MOD)-F(m-k,MOD)+MOD)%MOD; 44 return F(m-k,MOD); 45 } 46 if((a&1)&&(b%2==0)){ 47 if(k&1)return F(m-k,MOD); 48 return (F(m,MOD)-F(m-k,MOD)+MOD)%MOD; 49 } 50 if((a%2==0)&&(b&1))return (F(m,MOD)-F(k,MOD)+MOD)%MOD; 51 return F(k,MOD); 52 } 53 if(a&1){ 54 if(k&1)return F(m-k,MOD); 55 return (F(m,MOD)-F(m-k,MOD)+MOD)%MOD; 56 } 57 return F(k,MOD); 58 } 59 int main(){ 60 ll n,m,k; 61 cin>>n>>m>>k; 62 cout<<(calc(n+2,m,k)-1+k)%k<<endl; 63 return 0; 64 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号