动态规划--多边形游戏

　　

《算法分析与设计》 王晓东

问题描述：

　多边形游戏是一个单人玩的游戏，开始时有一个由n个顶点构成的多边形。每个顶点被赋予一个整数值，每条边被赋予一个运算符“+”或“*”。所有边依次用整数从1到n编号。

　　游戏第1步，将一条边删除。

　　随后n-1步按以下方式操作：

　　(1)选择一条边E以及由E连接着的2个顶点V1和V2；

　　(2)用一个新的顶点取代边E以及由E连接着的2个顶点V1和V2。将由顶点V1和V2的整数值通过边E上的运算得到的结果赋予新顶点。

　　最后，所有边都被删除，游戏结束。游戏的得分就是所剩顶点上的整数值。

　　问题:对于给定的多边形，计算最高得分。

如下图：

　　

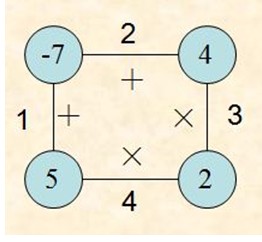
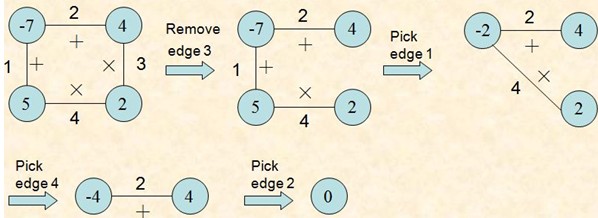
数据输入：

 第一行是一个整数N

第二行按照

边     顶点      边     顶点     ….     边     顶点

的顺序以此存放了N个顶点和N条边的标注信息。

 

问题求解：

　　

 　　当把一条边去除除后，再把它拉直，那么这个问题就可以变成一条链。那么就和以前写的矩阵连乘有几分的相似，其实我们最后要求的是这个链的表达式算式结果的最大值。于是我们就可以想到可以用数组p[i][j]来表示从点i开始，链长为j的算术表达式的最大值，用v[i]存储操作数，op[i]存储操作符。如果这条链的最后一次合并运算在op[i+s]处发生(1≤s≤j-1)，则可在op[i+s]处将链分割为2个子链p[i][s]和p[i+s][j-s]。似乎这样再按照以前解决动态规划题目时的思路，就可以解决问题了。   但是，我们再来考虑一下，由于有两种运算符+和x，并且操作数可能存在负数，那么我们也必须考虑两个负数相乘的结果可能比两个正数要打，所以我们同时还需要记录每个链的最大和最小值，然后判断，如果操作符为+的话，只需要两个链的最大值相加即可，如果操作符是x的话，那么必须把各种情况考虑进来，然后再求出最大值。分析如下：

　　设m1是对子链p[i][s]的任意一种合并方式得到的值，而a和b分别是在所有可能的合并中得到的最小值和最大值。m2是p[i+s][j-s]的任意一种合并方式得到的值，而c和d分别是在所有可能的合并中得到的最小值和最大值。依此定义有a≤m1≤b，c≤m2≤d

　　(1)当op[i+s]='+'时，显然有a+c≤m≤b+d

　　(2)当op[i+s]='*'时，有min{ac，ad，bc，bd}≤m≤max{ac，ad，bc，bd}

　　换句话说，主链的最大值和最小值可由子链的最大值和最小值得到。

于是我就用数组chain_value[i][j][2]来存储链的节点， chain_value[i][j][0]表示链的最大值，chain_value[i][j][1]表示链的最小值。

 

代码实现：

#include <stdio.h>
#include <stdlib.h>

#define MAX_POINT 20
int chain_value[MAX_POINT][MAX_POINT][2];  //chain[i][j][0]表示从v[i]节点开始，边长为j的链的最大值
                                           //chain[i][j][1]表示从v[i]节点开始，边长为j的链的最小值
int n,*v;
char *op;

int get_max_sum();
void chain_max(int start, int len, int k);
void get_max_min(int a, int b, int c, int d, int start, int index, int len);

int main()
{
    int i;
    char ch;

    scanf("%d",&n);
    v = (int *)malloc(n*sizeof(int));
    op = (char *)malloc(n*sizeof(char));

    ch = getchar();                    //数据输入
    for (i = 0; i < n; i++)
    {
        scanf("%c",&op[i]);
        ch = getchar();
        scanf("%d",&v[i]);
        ch = getchar();
    }

    printf("MAX:%d\n",get_max_sum());

    return 0;
}//main


int get_max_sum()
{
    int i,k,start,max,tmp,len;

    for (i = 0; i < n; i++)
    {
        chain_value[i][0][0] = v[i];        //链长为0，即单个点的值
        chain_value[i][0][1] = v[i];
    }
    
    for (len = 1; len < n; len++)  //控制链的长度，
    {
        for (start = 0; start < n ; start++)        //起点start配合链长，就可以得出除去某条边的效果
        {
            chain_value[start][len][0] = -9999;  
            chain_value[start][len][1] = 9999;
            for (k = 0; k < len; k++)
            {
                chain_max(start,len,k);
            }
        }
    }

    max = chain_value[0][n-1][0];            //最终的最大值
    for (start = 1; start < n; start++)
    {
        tmp =  chain_value[start][n-1][0];
        max = max > tmp ? max : tmp;
    }
    return max;
}

void chain_max( int start, int len, int k)
{
    int index,a,b,c,d;  //a<= m1 <= b  c<= m2 <=d

    index = (start+k+1)%n;  //表示符号(op)或者符号后面的操作数的下标
    
    a = chain_value[start][k][1];
    b = chain_value[start][k][0];
    c = chain_value[index][len-k-1][1];
    d = chain_value[index][len-k-1][0];
    
    get_max_min(a,b,c,d,start,index,len);

}

void get_max_min(int a, int b, int c, int d, int start, int index, int len)
{    
    int max_max,min_min,max_min,min_max;
    int max,min;

    max = chain_value[start][len][0];
    min = chain_value[start][len][1];

    if ('+' == op[index])
    { 
        max = max > (b + d) ? max : (b + d);
        min = min < (a + c) ? min : (a + c);
    }
    else if ('x' == op[index])
    {
        max_max = b * d;
        min_min = a * c;
        max_min = b * c;
        min_max = a * d;
                
        max = max > max_max ? max :max_max;
        max = max > min_min ? max : min_min;
        max = max > max_min ? max : max_min;
        max = max > min_max ? max : min_max;

        min = min < max_max ? min :max_max;
        min = min < min_min ? min : min_min;
        min = min < max_min ? min : max_min;
        min = min < min_max ? min : min_max;
    }

    chain_value[start][len][0] = max;  
    chain_value[start][len][1] = min;
}

//2013/9/14 10:13