欧拉函数

在1~N当中，与N互质的数的个数被叫做欧拉函数，简写成Φ(N)；

在算数基本定理中我们可以把一个数N分解成所有质因子的乘积的形式，记作

N = p1^a1 * p2^a2 *.... *pn^an;

所以欧拉函数的计算公式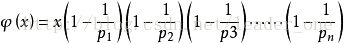 

 

1 欧拉函数定义

在数论中，对正整数n，欧拉函数φ(n)是小于或等于n的正整数中与n互质的数的数目。此函数以其首名研究者欧拉命名，它又称为φ函数（由高斯所命名）或是欧拉总计函数（totient function，由西尔维斯特所命名）。

例如φ(8) = 4，因为1,3,5,7均和8互质。

也可以从简化剩余系的角度来解释，简化剩余系(reduced residue system)也称既约剩余系或缩系，是m的完全剩余系中与m互素的数构成的子集，如果模m的一个剩余类里所有数都与m互素，就把它叫做与模m互素的剩余类。在与模m互素的全体剩余类中，从每一个类中各任取一个数作为代表组成的集合，叫做模m的一个简化剩余系。

（1，3，5，7）就构成了8的一个简化剩余系。

2 标准分解式

标准分解式：将质因数分解的结果，按照质因数大小，由小到大排列，并将相同质因数的连乘积，以指数形式表示，此种表示法称为标准分解式。

如2020的标准分解式是

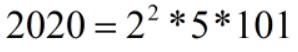
3 欧拉函数计算方法

（1）先化为标准分解式形式

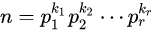
（2）再依照下式规则计算

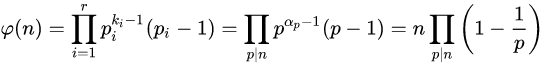
例如：