最小斯坦纳树学习笔记

本人非常菜如有错误请私信我指出

参考文献:

• \(《程序员的数学4——图论入门》\)

• $\ \([\)各类大佬写的笔记$](https://zzk.cnblogs.com/s?w=最小斯坦纳树问题)

---

建议先学习最小生成树和最短路算法

最小斯坦纳树(\(Minimum\ Steiner\ Tree\ Problem\))可以理解为升级版的最小生成树。

首先给定图 \(G=(V,E)\) ,以及 \(V\) 的子集 \(U\) ,\(U\) 中的点为终端节点。最小斯坦纳树即求包含所有终端节点的 \(G\) 的子树中用到边权总和最小的。

• 在最小斯坦纳树中，若所有顶点都为终端节点，这个问题就是最小生成树问题。

• 最小斯坦纳树已经被证明是 \(NP-Hard\) 问题，所以可能不存在高效算法

• 我很菜所以建议看看这篇$\Rightarrow $ Link

---

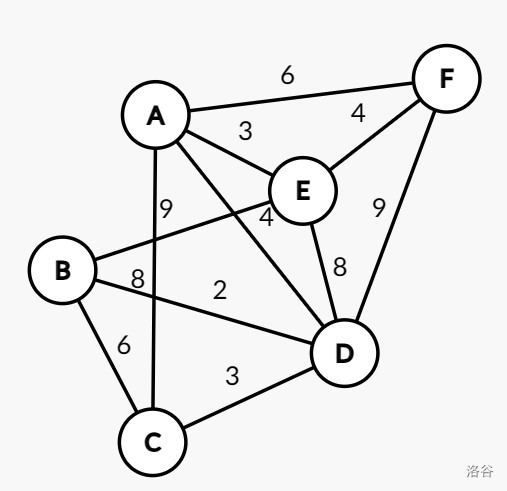
如上图 $\Uparrow $，已知其终端节点为 \(A,B,C,F\) ，则其最小斯坦纳树如下:

---

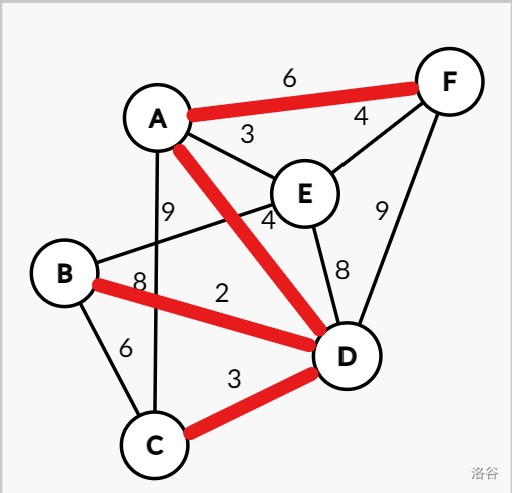
例题：P6192 【模板】最小斯坦纳树

题意：给定一个带权无向图和\(k\)
个定点，要求一个权值和最小的子图使得给定的所有点都在这个子图上并让这个子图权值最小。\(k≤10,n≤100,m≤500\)
。

思路:由于 \(k \leq 10\) ,所以可以考虑状压DP

可以将 \(dp_{i,s}\) 看作

考虑以下两种转移方式:

• \(dp_{i,S}=dp_{i,T}+dp_{i,S-T} \quad \quad (T\subseteq S )\)

• \(dp_{i,S}=dp_{i,s}+w(i,j)\)

显然只需枚举 \(S\) 的子集 \(T\) 即可,然后发现可以用最短路跑一边，于是故状压DP + dij/SPFA