【数学建模入门】TOPSIS法

TOPSIS法

背景知识

TOPSIS法（Technique for Order Preference by Similarity to Ideal Solution） 可翻译为逼近理想解排序法，国内常简称为优劣解距离法

与层次分析法相比，topsis的先决条件是有初始的数据，所以我们更应该通过这些数据进行分析

第一步：将原始矩阵正向化

最常见的四种指标：

指标名称	指标特点	例子
极大型（效益型）	越大越好	成绩、GDP
极小型（成本型）	越小越好	费用、污染程度
中间型	越接近某个值越好	水质量评估时的PH值
区间型	落在某个区间最好	体温、人体的血压

所谓正向化就是将所有指标转化为极大型指标

类型1：极小型-->极大型

姓名	成绩	处分次数	正向化后的处分次数
小王	78	0	4
小杨	89	2	2
小张	78	1	3
小吴	90	4	0
小曾	87	3	1

此时我们可以取正向化函数为：

\[f(x)=max-x \]

此时正向化完成，正向化函数可以不一致的

类型2：中间值型-->极大型

水样标本名称	PH	正向化后的指标
恒河水	10	0
泰晤士河水	8	0.6667
长江河水	7	1
密西西比河水	6	0.6667

（水样的PH值肯定越接近7越好）

\[假设{x_i}是一组中间值指标序列，且最佳的数值为x_{b}，那么正向化的公式如下： \]

\[M=max{|x_i-x_b|},x_i=1-|x_i-x_b|/M \]

类型3：区间型指标-->极大型指标

姓名	体温	正向化后的体温
张三	36.5	1
李四	37.9	0.4705
王五	35.1	0.4705
杨六	35.2	0.5294
曾七	38.7	0

一般人体的体温都是在36~37为正常，所以范围是[36,37]

公式化就是：

\[[x_i]是一组区间型指标，且最佳区间是[a,b],那么正向化公式是： \]

​ M=max{a-min(x),max(x)-b}

\[x_{i正向化后} = \begin{cases} 1-|x_i-a|/M,&x_i<a\\ 1,&a<=x_i<=b\\ 1-|x_i-b|/M,&x_i>b \end{cases} \]

此题中，M=1.7，最佳区间是[a,b]=[36,37].

第二步：正向化矩阵标准化

目的是消除不同指标量纲的影响。

假设有n个评价对象，m个评价指标（均已正向化）构成的正向化矩阵如下：

\[X= \left[ \begin{matrix} x_{11}& x_{12} & x_{13}&x_{14}&...&x_{1m} \\ x_{21}& x_{22} & x_{23}&x_{24}&...&x_{2m} \\ x_{31}& x_{32} & x_{33}&x_{34}&...&x_{3m} \\ ...&...&...&...&...&...\\ x_{n1}& x_{n2} & x_{n3}&x_{n4}&...&x_{nm} \end{matrix} \right] \]

那么就对，对其每一个元素标准化后的矩阵为Z，其中Z中的每个元素为：

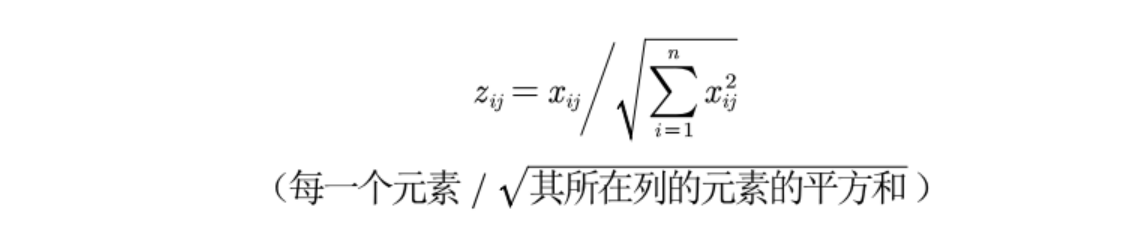
第三步：计算得分并归一化

有以下标准化矩阵：

\[Z= \left[ \begin{matrix} z_{11}& z_{12} & z_{13}&z_{14}&...&z_{1m} \\ z_{21}& z_{22} & z_{23}&z_{24}&...&z_{2m} \\ z_{31}& z_{32} & z_{33}&z_{34}&...&z_{3m} \\ ...&...&...&...&...&...\\ z_{n1}& z_{n2} & z_{n3}&z_{n4}&...&z_{nm} \end{matrix} \right] \]

计算得分公式的公式为：

这里的距离可以理解为向量之间的距离

定义最大值：

\[Z_{max}=(Z_{1max},Z_{2max},...,Z_{mmax})\\=(max\{z_{11},z_{21},z_{31},...,z_{n1}\},max\{z_{12},z_{22},z_{32},...,z_{n2}\},...,\\max\{z_{1m},z_{2m},z_{3m},...,z_{nm}\}) \]

定义最小值：

\[Z_{min}=(Z_{1min},Z_{2min},...,Z_{mmin})\\=(min\{z_{11},z_{21},z_{31},...,z_{n1}\},min\{z_{12},z_{22},z_{32},...,z_{n2}\},...,\\min\{z_{1m},z_{2m},z_{3m},...,z_{nm}\}) \]

定义第i个对象与最大值的距离（就是向量之间的距离的求法）：

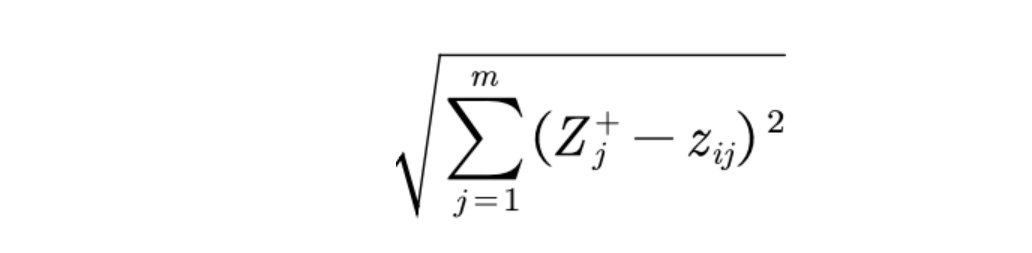
定义第i个对象与最大值的距离（就是向量之间的距离的求法）：

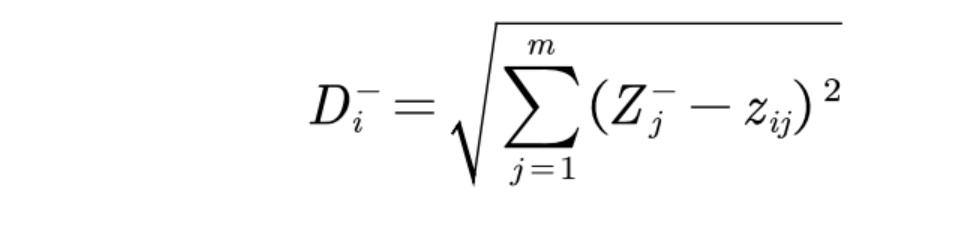
具体例子

姓名	成绩	处分次数	正向化后的处分次数
小王	78	0	4
小杨	89	2	2
小张	78	1	3
小吴	90	4	0
小曾	87	3	1

以此为例：

step1：正向化

易得已正向化

step2:标准化

由公式得以下矩阵：

姓名	成绩	正向化处分次数
小王	0.412	0.730
小杨	0.471	0.365
小张	0.412	0.548
小吴	0.476	0
小曾	0.460	0.183

step3:计算得分

最大的向量为[0.476,0.730]

最小的向量为[0.412,0]

有公式可以得

姓名	成绩	正向化处分次数	最小距离	最大距离	评分
小王	0.412	0.730	0.73	0.064	0.919
小杨	0.471	0.365	0.370	0.365	0.503
小张	0.412	0.548	0.548	0.193	0.740
小吴	0.476	0	0.064	0.73	0.081
小曾	0.460	0.183	0.189	0.547	0.257

归一化评分

0.368

0.201

0.296

0.032

0.103

由此可以得出小王的评分最高

带有权值topsis算法

有上题，成绩和处分次数真得一样重要吗？其实在现实生活中许多指标它们的权值是不一样的。

所以将权值引入topsis只需要改变第三步的公式，改变如下：

\[w_j代表第j个指标的权值， \]

将如下公式改为

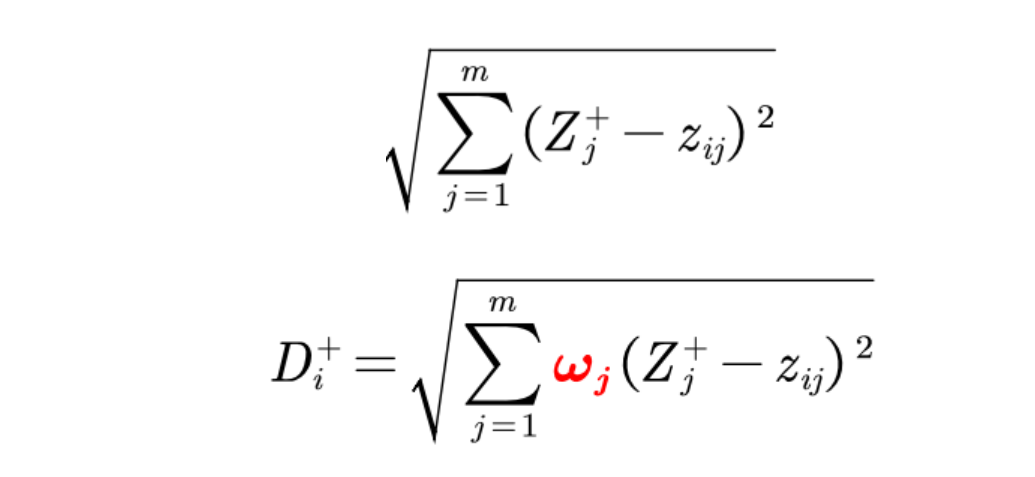
最小距离同上

而权值可以根据层次分析法