图论
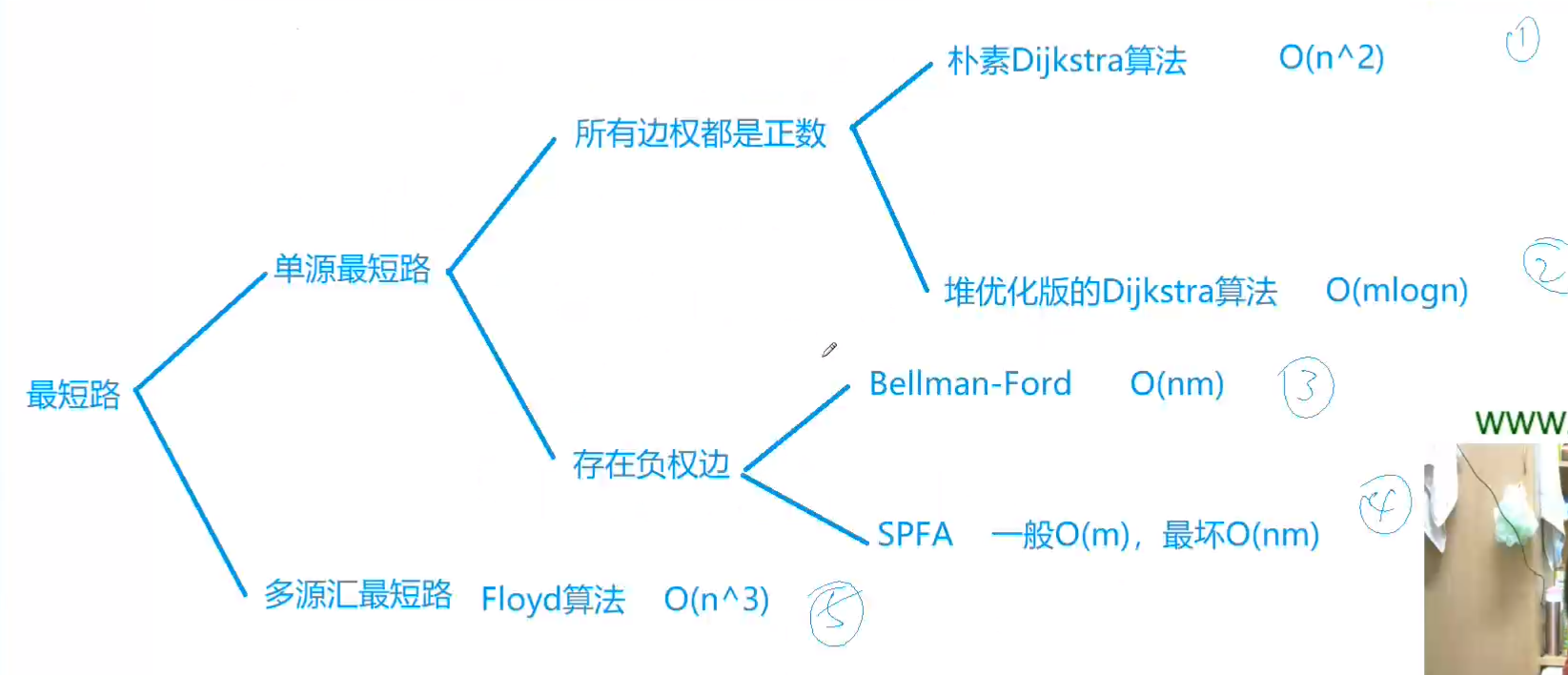
![最短路.png]()
链式前向星
//邻接表,稀疏图
const int N = 100010, M = N * 2;
int h[N], e[M], ne[M], idx;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
Dijkstra
朴素版(找节点)
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510;
int n, m;
int g[N][N];
int dist[N];
bool st[N];
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n - 1; i ++ )
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], dist[t] + g[t][j]);
st[t] = true;
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main()
{
scanf("%d%d", &n, &m);
memset(g, 0x3f, sizeof g);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
g[a][b] = min(g[a][b], c);
}
printf("%d\n", dijkstra());
return 0;
}
堆版(找边)
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 100010; // 把N改为150010就能ac
// 稀疏图用邻接表来存
int h[N], e[N], ne[N], idx;
int w[N]; // 用来存权重
int dist[N];
bool st[N]; // 如果为true说明这个点的最短路径已经确定
int n, m;
void add(int x, int y, int c)
{
// 有重边也不要紧,假设1->2有权重为2和3的边,再遍历到点1的时候2号点的距离会更新两次放入堆中
// 这样堆中会有很多冗余的点,但是在弹出的时候还是会弹出最小值2+x(x为之前确定的最短路径),
// 并标记st为true,所以下一次弹出3+x会continue不会向下执行。
w[idx] = c;
e[idx] = y;
ne[idx] = h[x];
h[x] = idx++;
}
int dijkstra()
{
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap; // 定义一个小根堆
// 这里heap中为什么要存pair呢,首先小根堆是根据距离来排的,所以有一个变量要是距离,
// 其次在从堆中拿出来的时候要知道知道这个点是哪个点,不然怎么更新邻接点呢?所以第二个变量要存点。
heap.push({ 0, 1 }); // 这个顺序不能倒,pair排序时是先根据first,再根据second,
// 这里显然要根据距离排序
while(heap.size())
{
PII k = heap.top(); // 取不在集合S中距离最短的点
heap.pop();
int ver = k.second, distance = k.first;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i]; // i只是个下标,e中在存的是i这个下标对应的点。
if(dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({ dist[j], j });
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
int main()
{
memset(h, -1, sizeof(h));
scanf("%d%d", &n, &m);
while (m--)
{
int x, y, c;
scanf("%d%d%d", &x, &y, &c);
add(x, y, c);
}
cout << dijkstra() << endl;
return 0;
}
bellman-ford(边数限制最多经过 k 条边)
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510, M = 10010;
struct Edge {
int a;
int b;
int w;
} e[M];//把每个边保存下来即可
int dist[N];
int back[N];//备份数组防止串联
int n, m, k;//k代表最短路径最多包涵k条边
int bellman_ford() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < k; i++) {//k次循环
memcpy(back, dist, sizeof dist);
for (int j = 0; j < m; j++) {//遍历所有边
int a = e[j].a, b = e[j].b, w = e[j].w;
dist[b] = min(dist[b], back[a] + w);
//使用backup:避免给a更新后立马更新b, 这样b一次性最短路径就多了两条边出来
}
}
if (dist[n] > 0x3f3f3f3f / 2) return -1;
else return dist[n];
}
int main() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 0; i < m; i++) {
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
e[i] = {a, b, w};
}
int res = bellman_ford();
if (res == -1) puts("impossible");
else cout << res;
return 0;
}
Floyd
#include <iostream>
using namespace std;
const int N = 210, M = 2e+10, INF = 1e9;
int n, m, k, x, y, z;
int d[N][N];
void floyd() {
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
int main() {
cin >> n >> m >> k;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if(i == j) d[i][j] = 0;
else d[i][j] = INF;
while(m--) {
cin >> x >> y >> z;
d[x][y] = min(d[x][y], z);
//注意保存最小的边
}
floyd();
while(k--) {
cin >> x >> y;
if(d[x][y] > INF/2) puts("impossible");
//由于有负权边存在所以约大过INF/2也很合理
else cout << d[x][y] << endl;
}
return 0;
}
spfa
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 100010;
int h[N], e[N], w[N], ne[N], idx;//邻接表,存储图
int st[N];//标记顶点是不是在队列中
int dist[N];//保存最短路径的值
int q[N], hh, tt = -1;//队列
void add(int a, int b, int c){//图中添加边和边的端点
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void spfa(){
q[++tt] = 1;//从1号顶点开始松弛,1号顶点入队
dist[1] = 0;//1号到1号的距离为 0
st[1] = 1;//1号顶点在队列中
while(tt >= hh){//不断进行松弛
int a = q[hh++];//取对头记作a,进行松弛
st[a] = 0;//取完队头后,a不在队列中了
for(int i = h[a]; i != -1; i = ne[i])//遍历所有和a相连的点
{
int b = e[i], c = w[i];//获得和a相连的点和边
if(dist[b] > dist[a] + c){//如果可以距离变得更短,则更新距离
dist[b] = dist[a] + c;//更新距离
if(!st[b]){//如果没在队列中
q[++tt] = b;//入队
st[b] = 1;//打标记
}
}
}
}
}
int main(){
memset(h, -1, sizeof h);//初始化邻接表
memset(dist, 0x3f, sizeof dist);//初始化距离
int n, m;//保存点的数量和边的数量
cin >> n >> m;
for(int i = 0; i < m; i++){//读入每条边和边的端点
int a, b, w;
cin >> a >> b >> w;
add(a, b, w);//加入到邻接表
}
spfa();
if(dist[n] == 0x3f3f3f3f )//如果到n点的距离是无穷,则不能到达
cout << "impossible";
else cout << dist[n];//否则能到达,输出距离
return 0;
}
最小生成树
Prim
#include <iostream>
#include <cstring>
using namespace std;
const int N = 505, INF = 0x3f3f3f3f;
int n, m;
int g[N][N];
int dist[N];
bool st[N];
int prim()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0; // 第一个点一定在最小生成树中
int res = 0; // 用来存放权值之和
for(int i = 0; i < n; i ++)
{
int t = -1;
for(int j = 1; j <= n; j ++)
if(!st[j] && (t == -1 || dist[j] < dist[t]))
t = j;
if(dist[t] == INF) return INF; // 尽早跳出循环防止TLE,如果不加则需要在输出的地方更改
res += dist[t];
st[t] = true;
for(int j = 1; j <= n; j ++)
dist[j] = min(dist[j], g[t][j]); // 注意和dijkstra的区别
// prim的dist是到已经生成的树的最短距离
}
return res;
}
int main()
{
cin >> n >> m;
memset(g, 0x3f, sizeof g);
while(m --)
{
int a, b, c;
cin >> a >> b >> c;
g[a][b] = g[b][a] = min(g[a][b], c);
}
int t = prim();
if(t == INF) cout << "impossible" << endl; // 如果上面不及时跳出循环则在这里改为(t >= INF / 2)
else cout << t << endl;
return 0;
}
Kruskal
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, M = 200010, INF = 0x3f3f3f3f;
int n, m;
int p[N];
struct Edge
{
int a, b, w;
bool operator< (const Edge &W)const
{
return w < W.w;
}
}edges[M];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal()
{
sort(edges, edges + m);
for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集
int res = 0, cnt = 0;
for (int i = 0; i < m; i ++ )
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if (a != b)
{
p[a] = b;
res += w;
cnt ++ ;
}
}
if (cnt < n - 1) return INF;
return res;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < m; i ++ )
{
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
edges[i] = {a, b, w};
}
int t = kruskal();
if (t == INF) puts("impossible");
else printf("%d\n", t);
return 0;
}
二分图
染色法
/*
开始对任意一未染色的顶点染色。
判断其相邻的顶点中,若未染色则将其染上和相邻顶点不同的颜色。
若已经染色且颜色和相邻顶点的颜色相同则说明不是二分图,若颜色不同则继续判断。
bfs和dfs可以搞定!
*/
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010 * 2;
int e[N], ne[N], idx;//邻接表存储图
int h[N];
int color[N];//保存各个点的颜色,0 未染色,1 是红色,2 是黑色
int n, m;//点和边
void add(int a, int b)//邻接表插入点和边
{
e[idx] = b, ne[idx]= h[a], h[a] = idx++;
}
bool dfs(int u, int c)//深度优先遍历
{
color[u] = c;//u的点成 c 染色
//遍历和 u 相邻的点
for(int i = h[u]; i!= -1; i = ne[i])
{
int b = e[i];
if(!color[b])//相邻的点没有颜色,则递归处理这个相邻点
{
if(!dfs(b, 3 - c)) return false;//(3 - 1 = 2, 如果 u 的颜色是2,则和 u 相邻的染成 1)
//(3 - 2 = 1, 如果 u 的颜色是1,则和 u 相邻的染成 2)
}
else if(color[b] && color[b] != 3 - c)//如果已经染色,判断颜色是否为 3 - c
{
return false;//如果不是,说明冲突,返回
}
}
return true;
}
int main()
{
memset(h, -1, sizeof h);//初始化邻接表
cin >> n >> m;
for(int i = 1; i <= m; i++)//读入边
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
for(int i = 1; i <= n; i++)//遍历点
{
if(!color[i])//如果没染色
{
if(!dfs(i, 1))//染色该点,并递归处理和它相邻的点
{
cout << "No" << endl;//出现矛盾,输出NO
return 0;
}
}
}
cout << "Yes" << endl;//全部染色完成,没有矛盾,输出YES
return 0;
}
匈牙利算法
#include<iostream>
#include <cstring>
#include<algorithm>
using namespace std;
// 邻接表存储图
int n1, n2, m;
int h[500], e[100010],ne[100010], idx = 0;
//st 标记是否递归找过, match[x]:和 x 编号的男生的编号
int st[510], match[510];
//存图函数
void add(int a, int b){
e[idx] = b, ne[idx] = h[a]; h[a] = idx++;
}
//递归找可以匹配的点
bool find(int x){
// 和各个点尝试能否匹配
for(int i = h[x]; i != -1; i = ne[i]){
int b = e[i];
if(!st[b]){//打标记
st[b] = 1;
// 当前尝试点没有被匹配或者和当前尝试点匹配的那个点可以换另一个匹配
if(match[b] == 0 || find(match[b])){
// 和当前尝试点匹配在一起
match[b] = x;
return true;
}
}
}
return false;
}
int main(){
memset(h, -1, sizeof h);
cin >> n1 >> n2 >> m;
// 保存图,因为只从一遍找另一边,所以该无向图只需要存储一个方向
for(int i = 0; i < m; i++){
int a, b;
cin >> a >> b;
add(a, b);
}
int res = 0;
//为各个点找匹配
for(int i = 1; i <= n1; i++){
memset(st, 0, sizeof st);
//找到匹配
if(find(i)) res++;
}
cout << res;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号