【图论·树】HDU 4340 Capturing a country（树形DP）

一开始想的状态是dp[i][0/1][0/1]表示i点被A还是被B走到，该点有没有折扣，其实第三维定义是冗余的，有折扣肯定比没折扣好。
由于A和B的路径中必须得有一个无折扣点，所以可以定义一下一个维度表示这个无折扣点在i的上面还是下面还是它本身。

每个节点为根的子树，有可能是：
A从根的【上面】攻击下来，
A从【根或下面】攻击到根上面，
B从根的【上面】攻击下来，
B从【根或下面】攻击到根上面。
于是设计状态
dp[i][0..1][0..1]分别对应i为根的子树上面四种状态下攻击整个子树的最小代价。
转移思路见下图

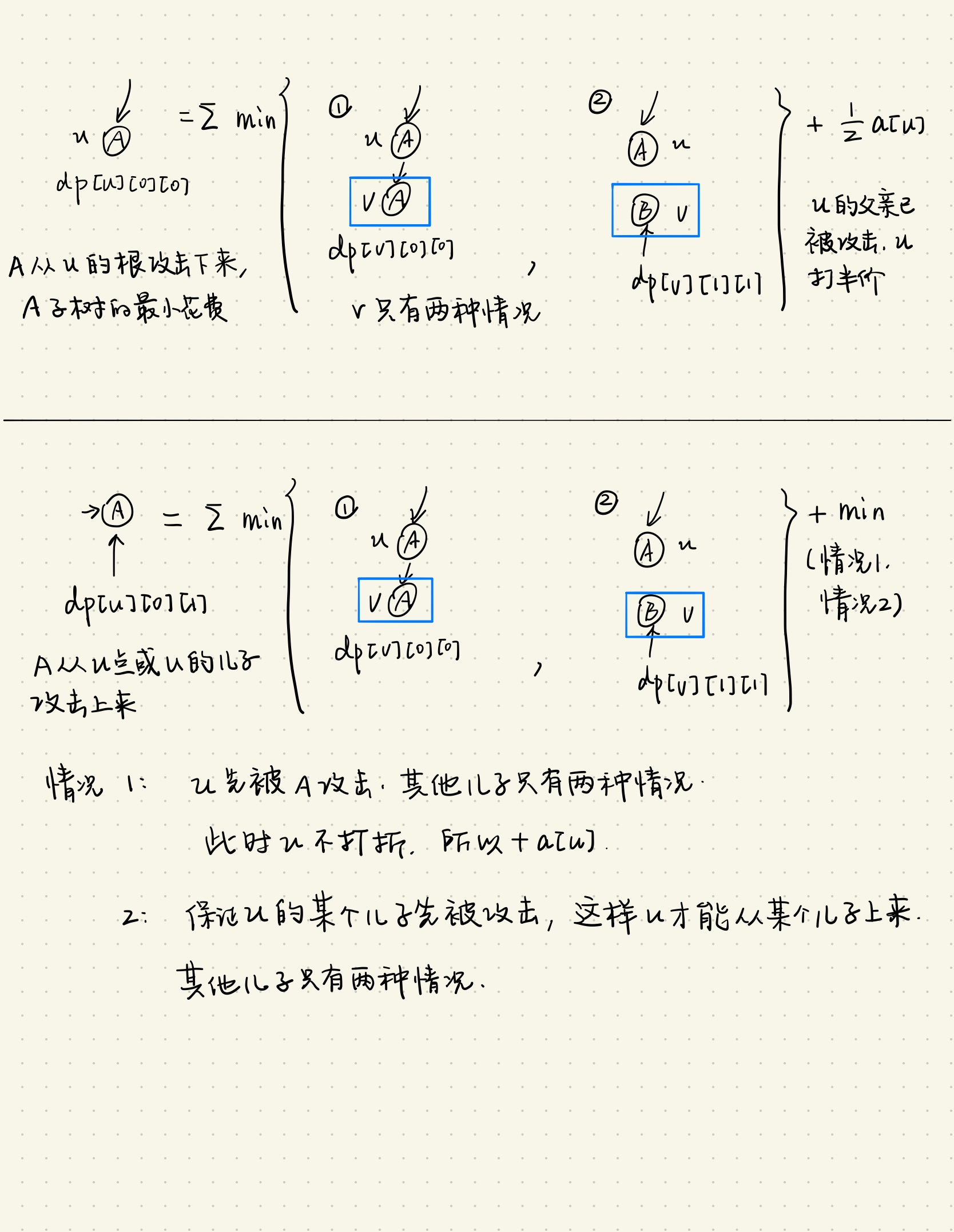
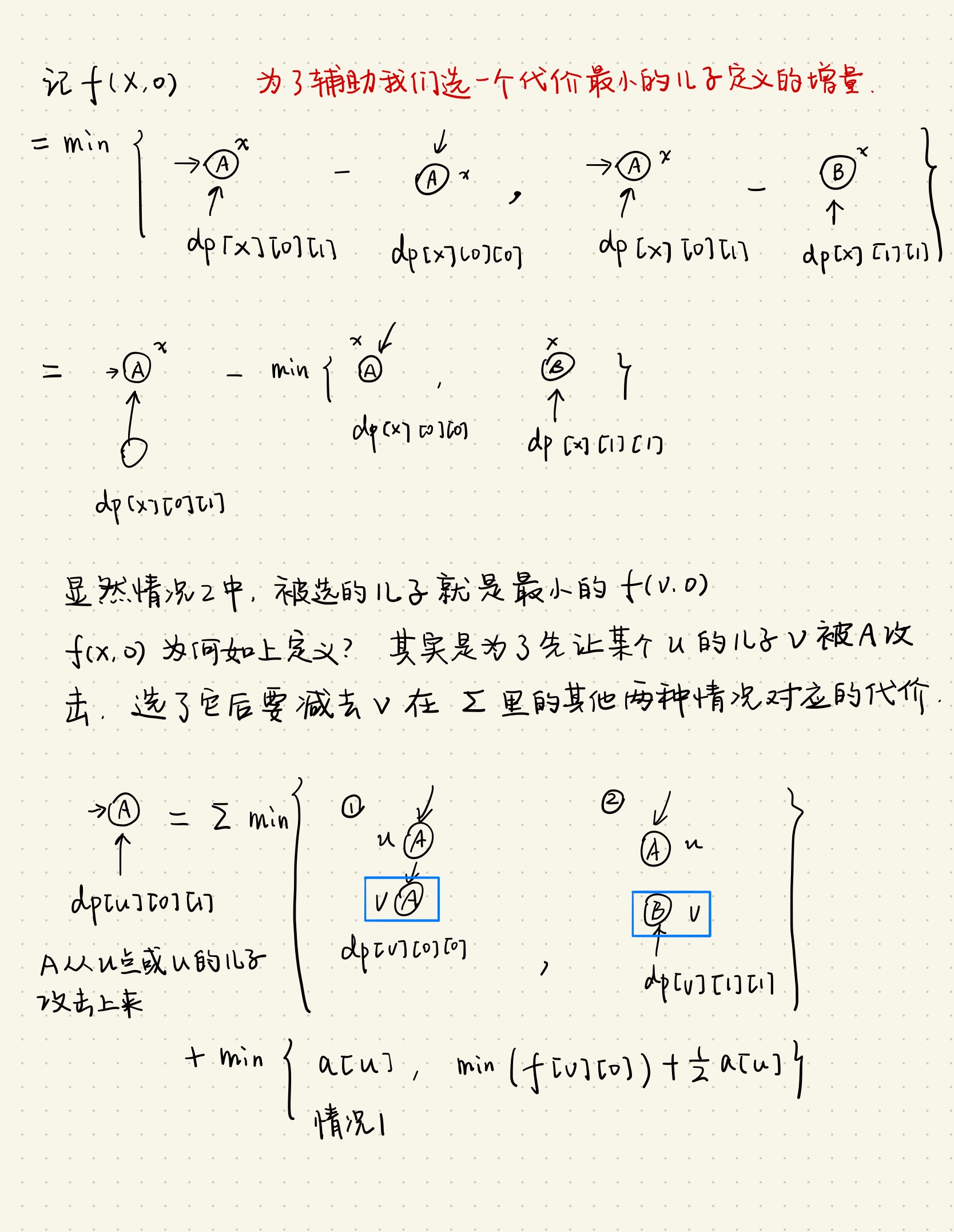
代码和思路参考了：https://www.cnblogs.com/flipped/p/HDU4340.html

#include<bits/stdc++.h>
using namespace std;
const int N=101;
const int INF=0x3f3f3f3f;
int n,a[N],b[N],dp[N][2][2],f[N][2];
vector<int> e[N];

void dfs(int u,int fa)
{
	int sa=0,sb=0;
	for(int i=0;i<e[u].size();i++)
	{
		int v=e[u][i];
		if(v==fa)continue;
		dfs(v,u);
		f[u][0]=min(f[u][0],f[v][0]);
		f[u][1]=min(f[u][1],f[v][1]);
		sa+=min(dp[v][0][0],dp[v][1][1]);
		sb+=min(dp[v][1][0],dp[v][0][1]);
	}
	dp[u][0][0]=sa+a[u]/2;
	dp[u][1][0]=sb+b[u]/2;
	
	dp[u][0][1]=sa+min(a[u],f[u][0]+a[u]/2);
	dp[u][1][1]=sb+min(b[u],f[u][1]+b[u]/2);
	
	f[u][0]=dp[u][0][1]-min(dp[u][0][0],dp[u][1][1]);
	f[u][1]=dp[u][1][1]-min(dp[u][1][0],dp[u][0][1]);
}

void init()
{
	memset(dp,0,sizeof(dp));
	memset(f,INF,sizeof(f));
	for(int i=1;i<=n;i++)e[i].clear();
}
int main()
{
	while(~scanf("%d",&n))
	{
		init();
		for(int i=1;i<=n;i++)scanf("%d",&a[i]);
		for(int i=1;i<=n;i++)scanf("%d",&b[i]);
		for(int i=1;i<n;i++)
		{
			int x,y;scanf("%d%d",&x,&y);
			e[x].push_back(y);
			e[y].push_back(x);
		}
		dfs(1,0);
		printf("%d\n",min(dp[1][0][1],dp[1][1][1]));
	}
	
	return 0;
}