数据结构基础第6讲
数据结构基础第6讲 图及其应用
1-2个选择

考点一:图的基本概念
1.图基本概念
-
连通图:
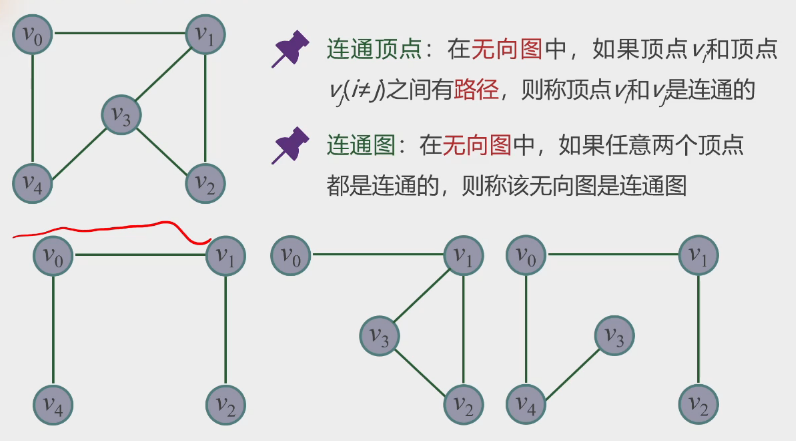
-
极大连通子图-连通分量:
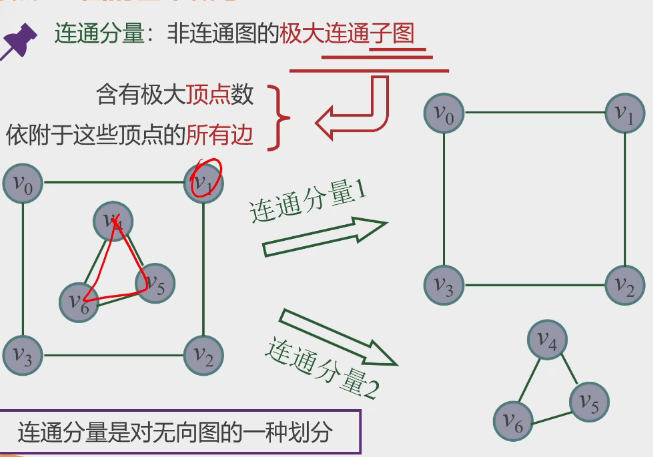
-
极小连通子图-生成树:
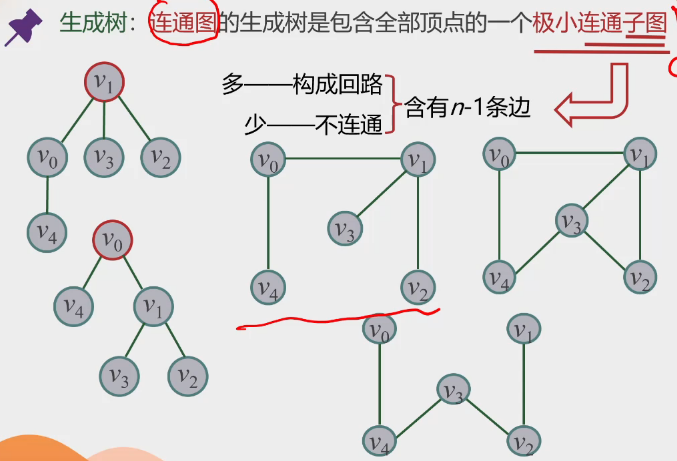
-
强连通顶点
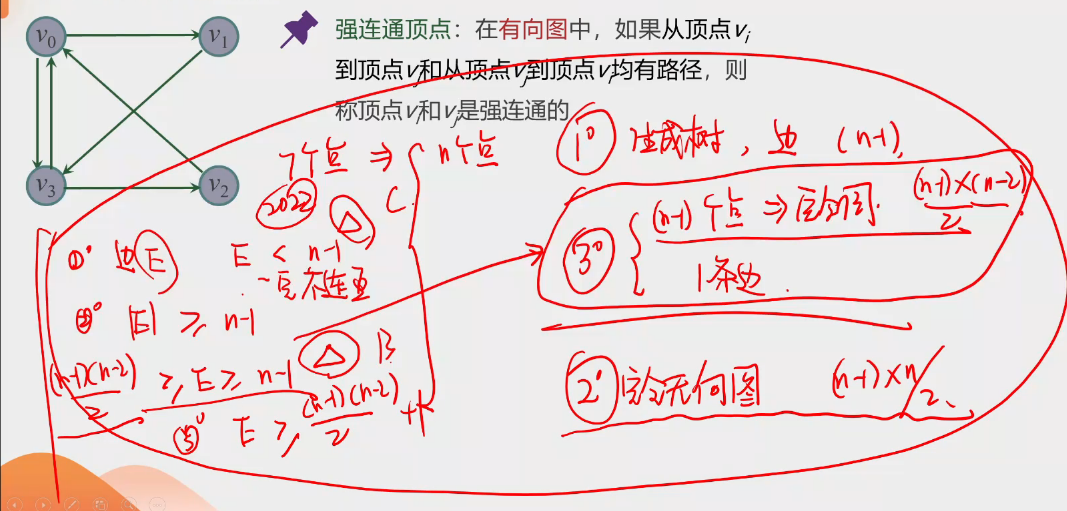
给定n个顶点,要保证图在任何情况下连通需要最小边数:
- 1.生成树,边(n-1)
- 2.完全无向图\(\frac{(n-1)\times n}{2}\)
- 3.\(\left \{ \begin{matrix} (n-1)个点 \Rightarrow 完全图 \frac{(n-1)\times (n-2)}{2} \\ 1条边 \end{matrix} \right .\)
边设为E,\(E < n-1\) 一定不连通
\(|E|\geqslant(n-1)不一定\\ \frac{(n-1) \times(n-2)}{2}\geqslant E \geqslant n-1\)
\(E\geqslant\frac{(n-1)(n-2)}{2}+1\)一定连通
考点二:图的存储
1.邻接矩阵

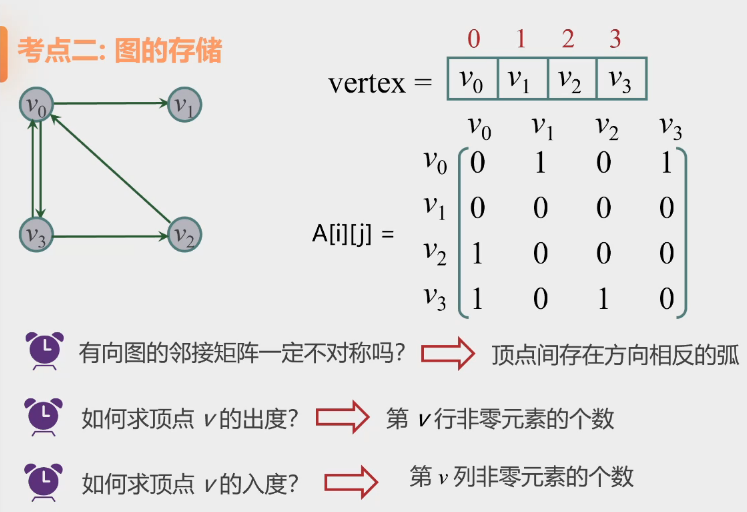
2.邻接矩阵的特性

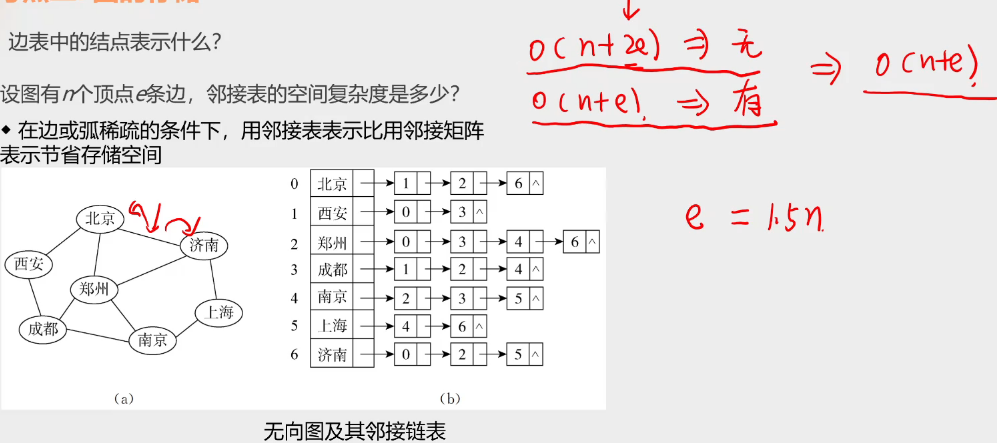
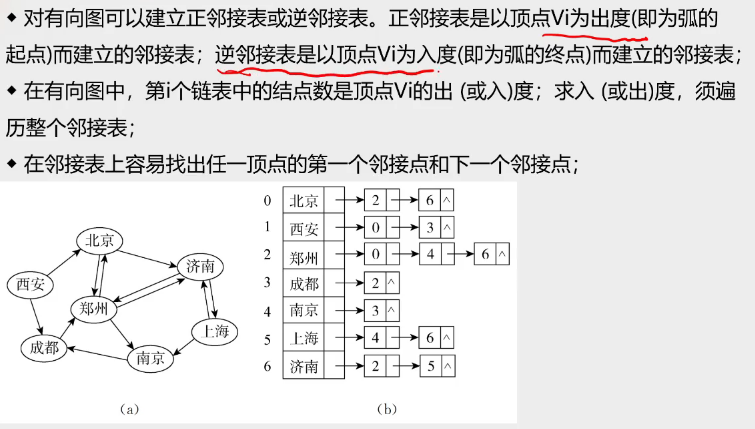
3.邻接表
-
邻接表概述
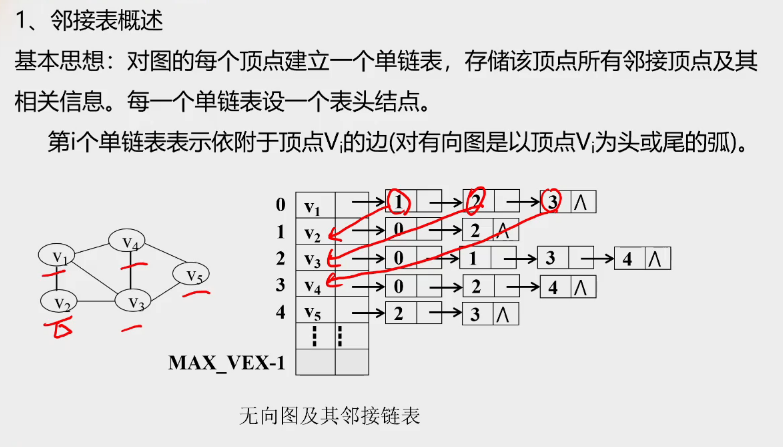
-
邻接表结点结构

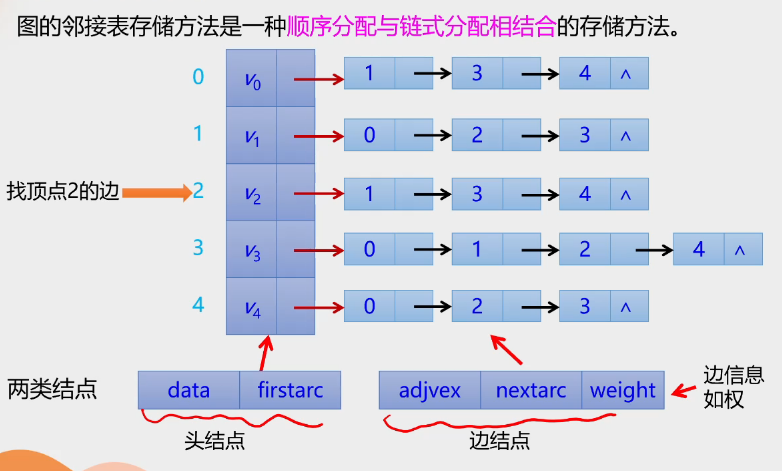
-
邻接表特点
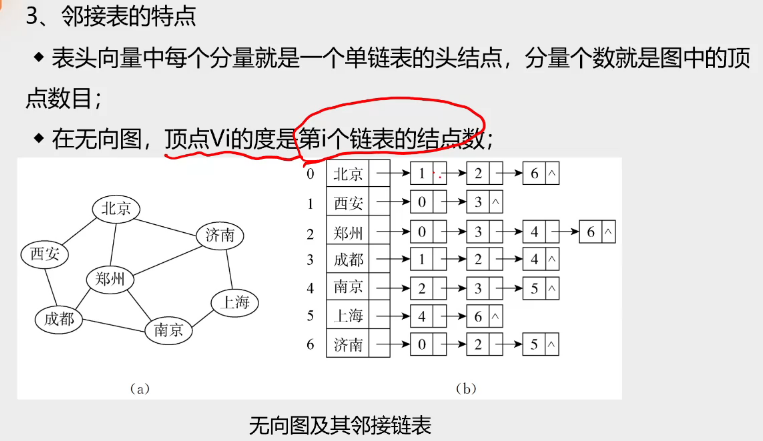
考点三:图的遍历
1.深度优先DFS

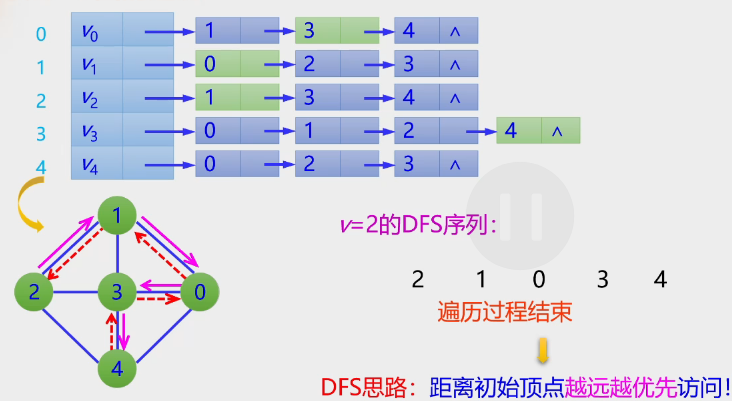
一些规律:
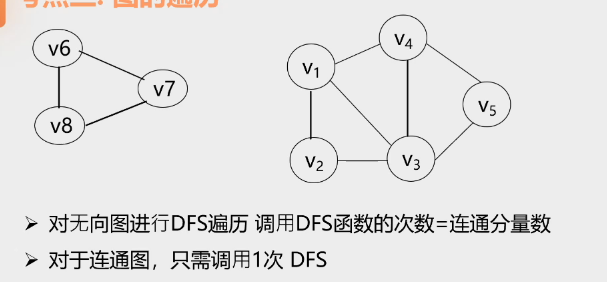
算法分析:

2.深度优先遍历生成树
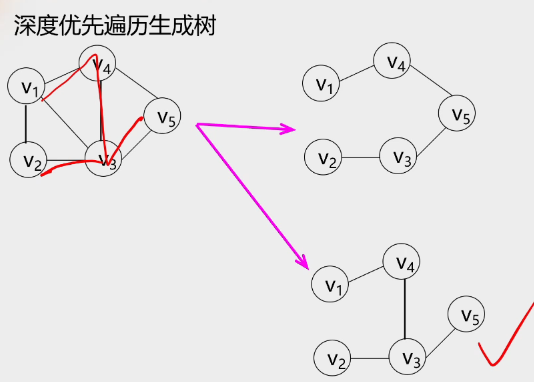
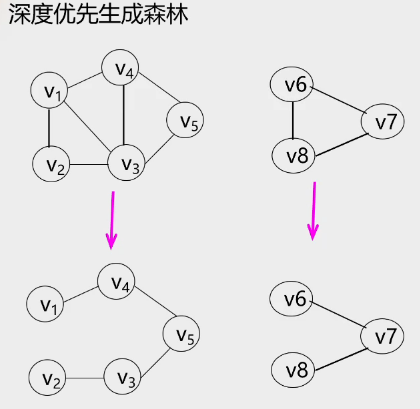
3.广度优先

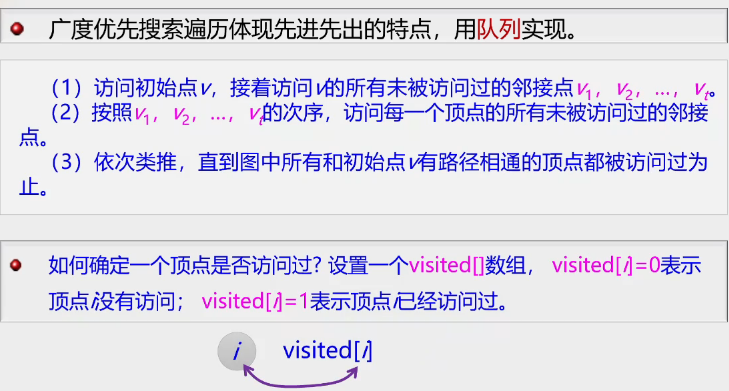
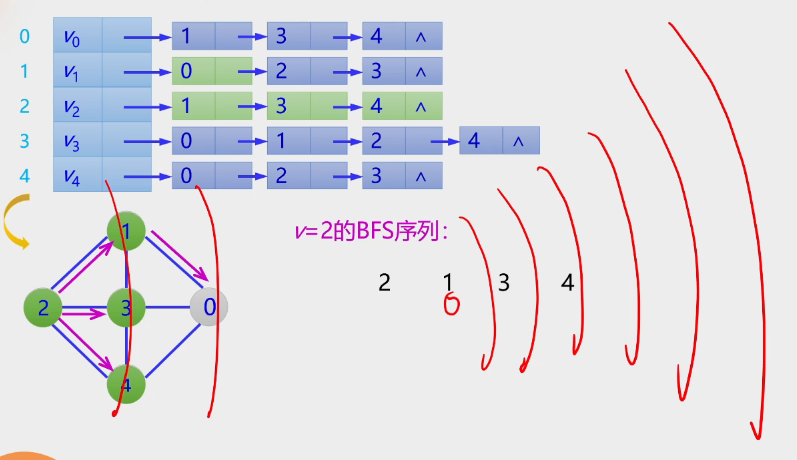
当一个点先遍历,下一层的点从它先出发
结论:

算法分析:

4.广度优先遍历生成树
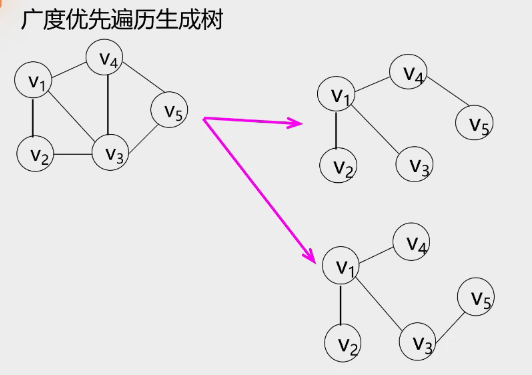
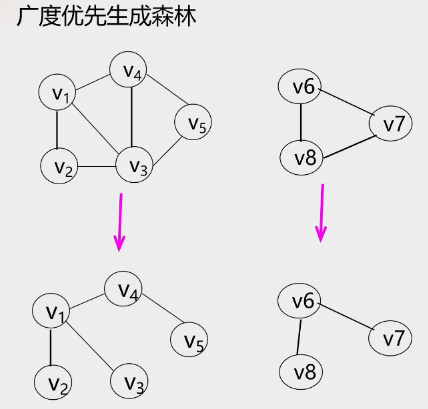
5.关于图遍历

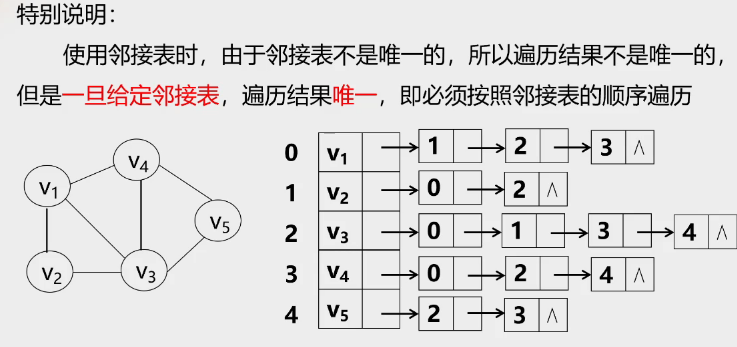
考点四:最小生成树
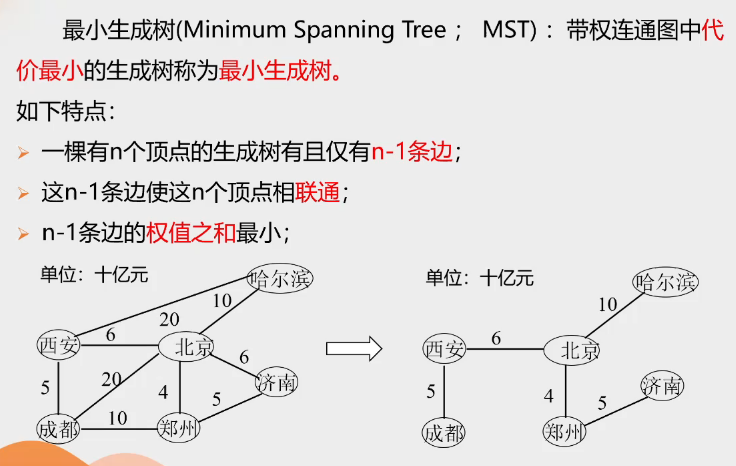
1.Prim算法(贪吃蛇)
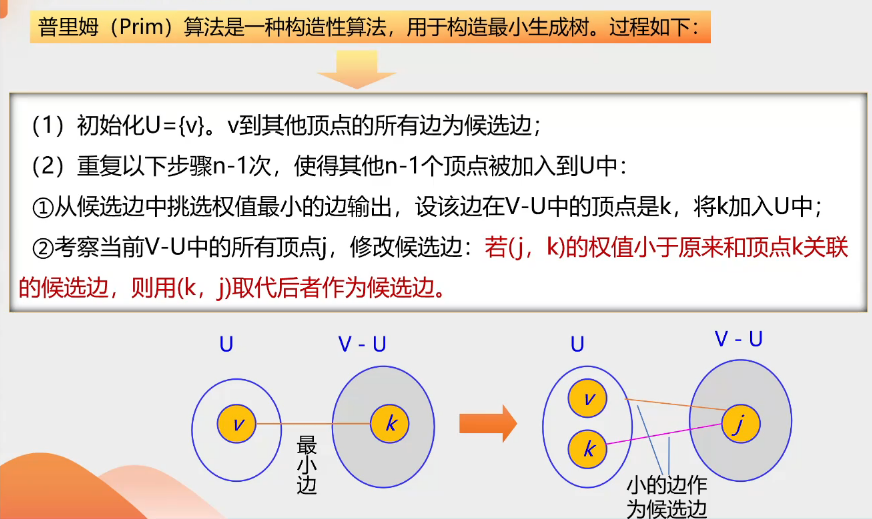
- 算法演示过程
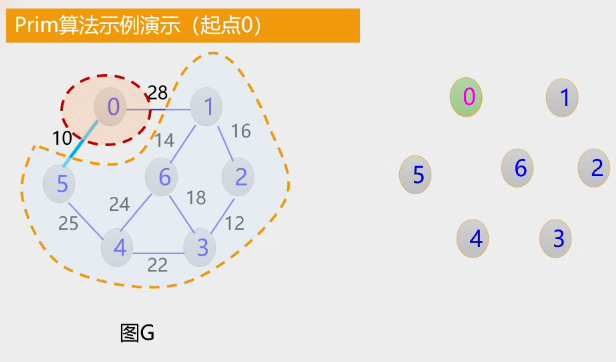
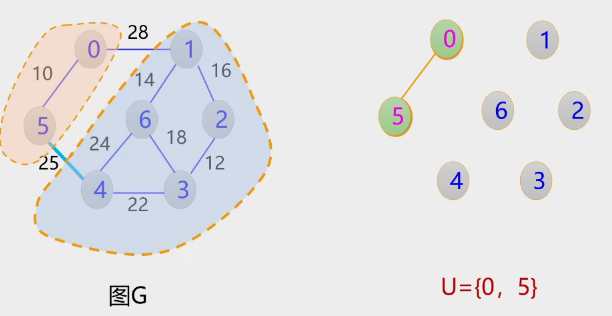
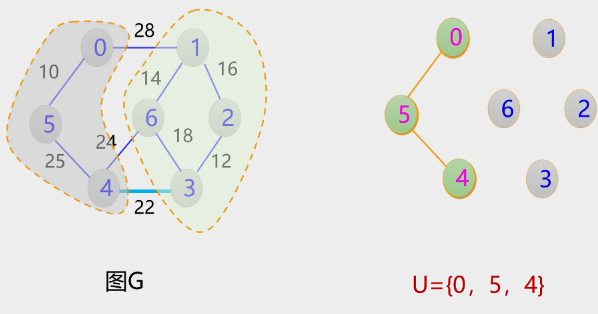
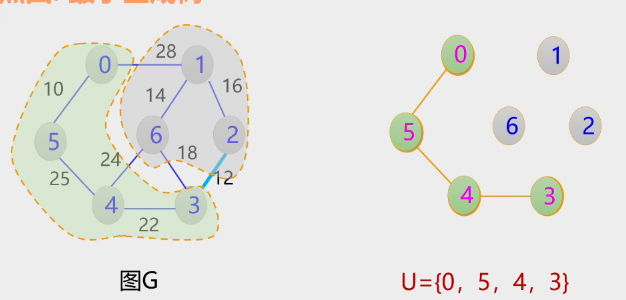
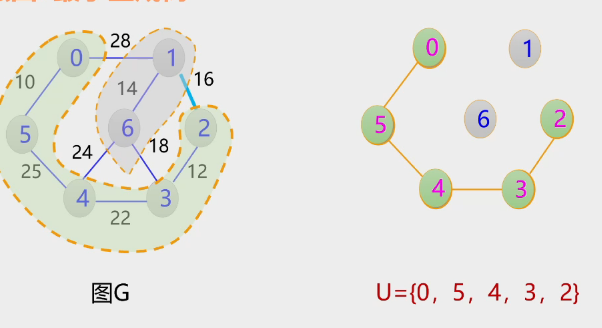
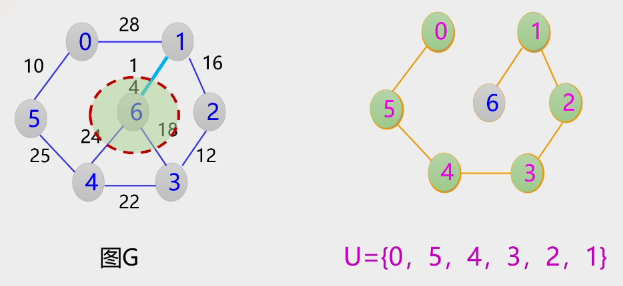

2.Kruskal算法

- 算法过程:
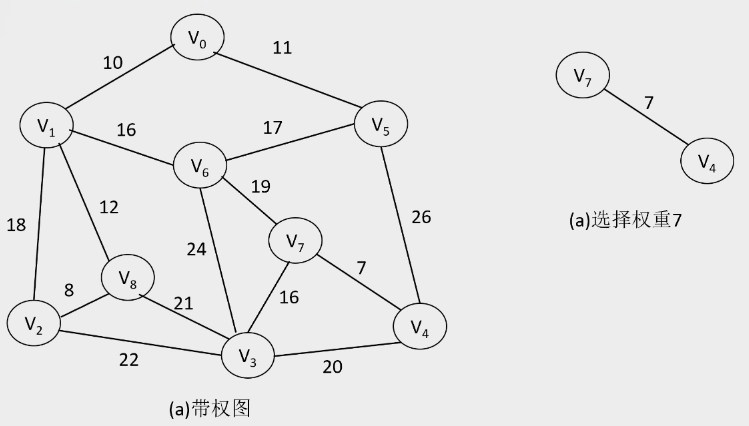
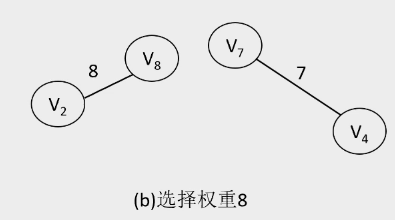
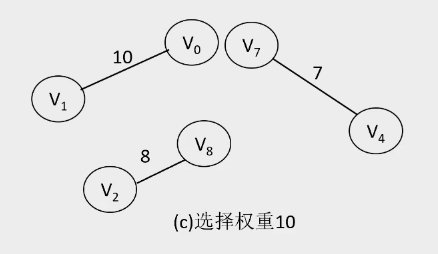
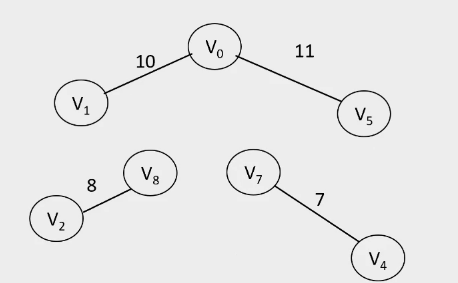
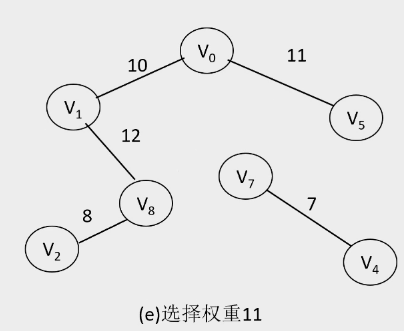
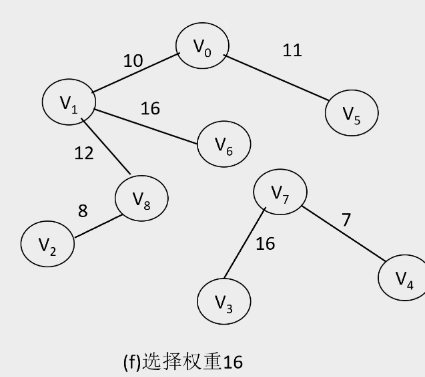
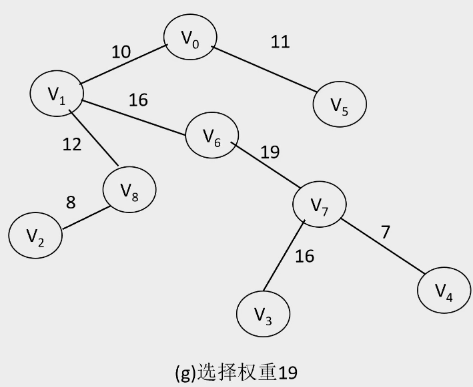
-
合并子树问题:
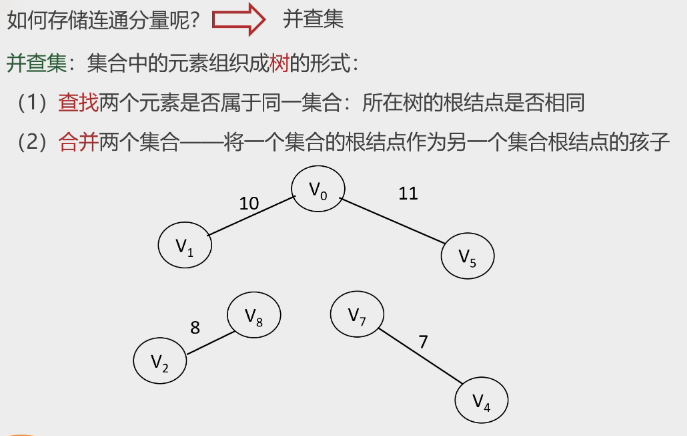
-
算法分析:

-
最小生成树唯一性:

在遇到相同权值时会有不同选法

考点五:最短路径
1.路径

2. Dijkstra算法:单源点最短路径问题 \(\bigstar\)
-
问题描述
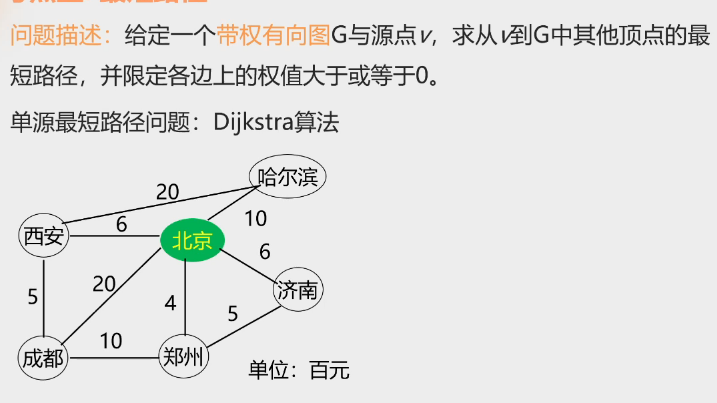
-
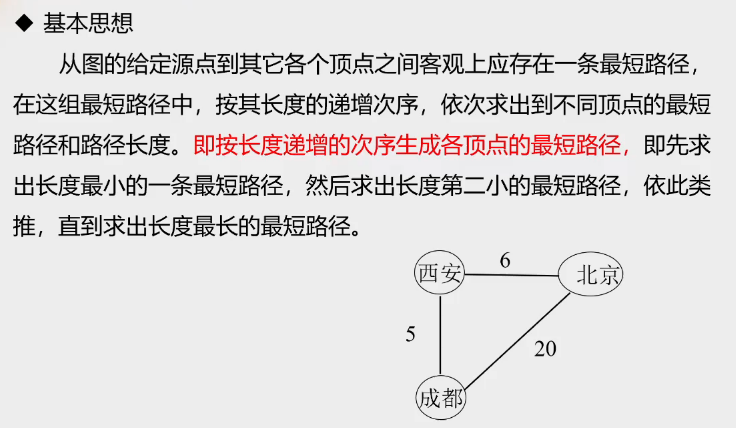
基本思想
按长度递增的次序生成各顶点的最短路径
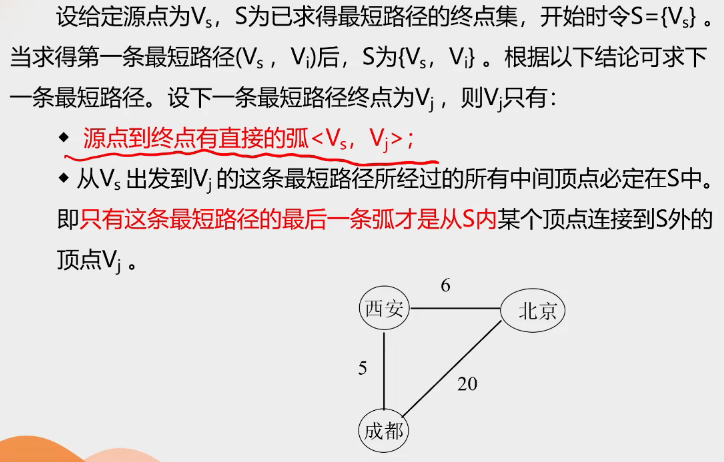
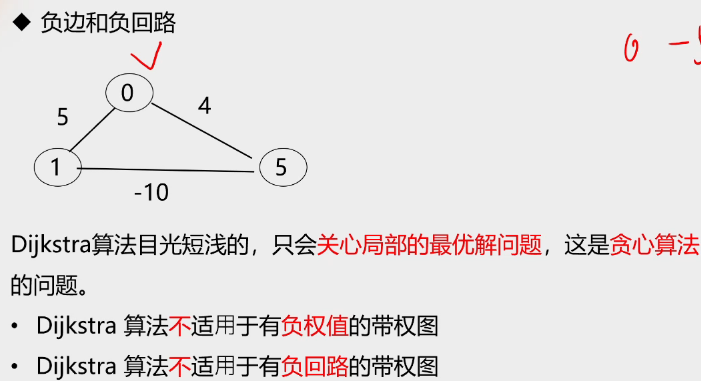
不适合有负权的边,也不适合有负回路
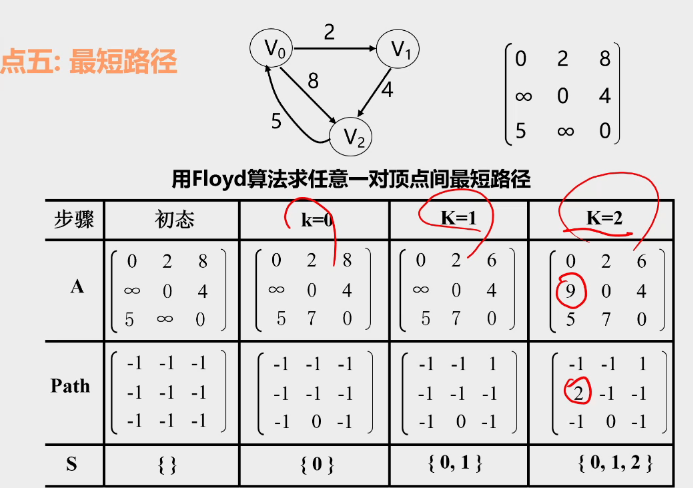
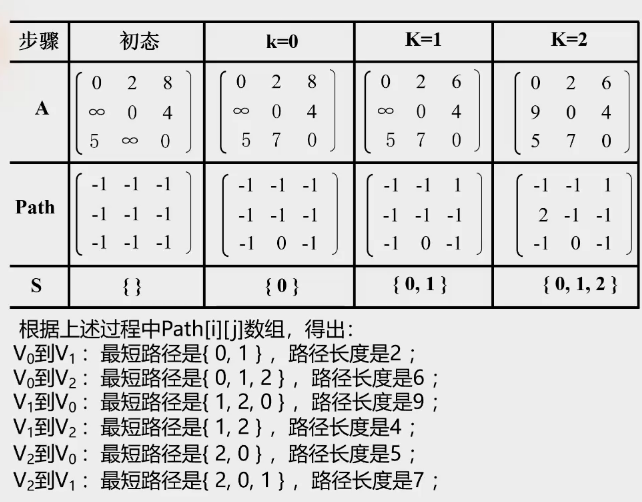
3.Floyd算法
-
算法实现:

当K=0表示经过\(v_0\),当K=1表示经过\(v_1\),当K=2表示经过\(v_2\)
-
算法分析

无法解决负权回路

考点六:AOV网和拓扑排序
1.用点表示活动的网,用边表示活动先后顺序,叫AOV网

2.拓扑排序
按其顶点的先后顺序将其整到一个序列中,且满足1,2

-
过程:
找到入度为0的结点去掉它及他的边;剩余点同理,由此得到的序列就是拓扑序列
-
拓扑序列唯一性问题
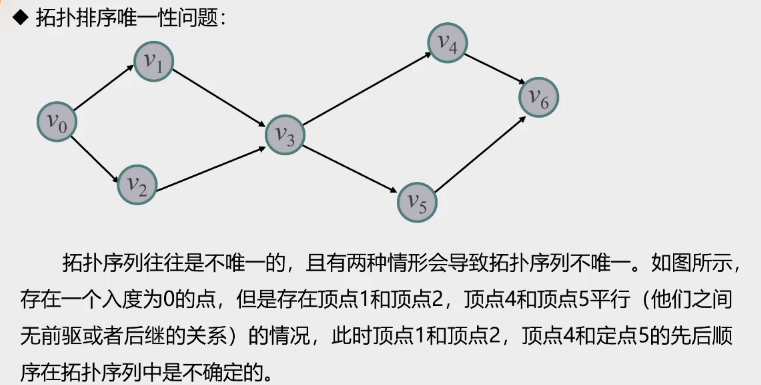
当存在平行边时一定不唯一
存在多个入度为0的点,也不唯一
有环一定没有拓扑序列
考点七:AOE网和关键路径
1.AOE网
用边表示活动
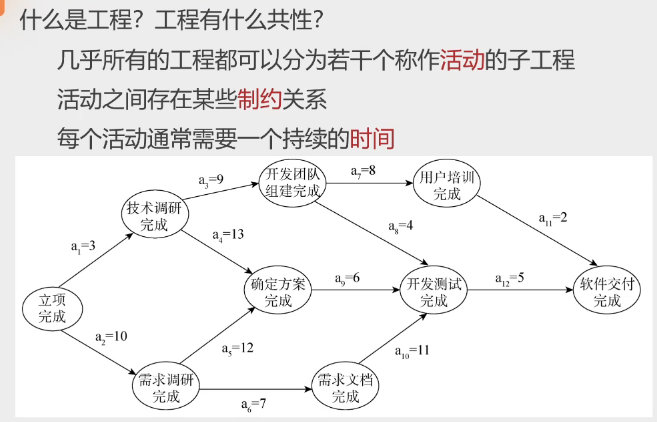

2.AOE网的性质

3.关键路径和关键活动
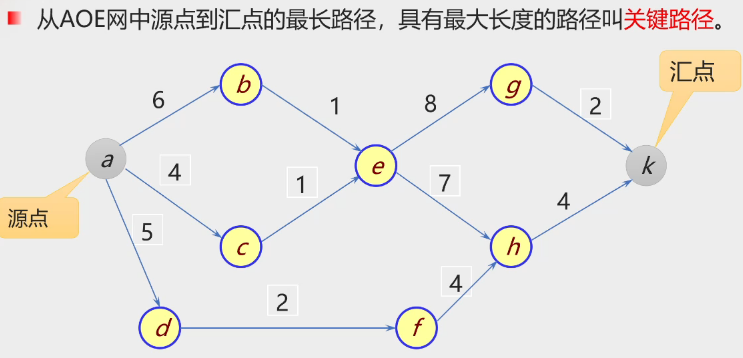

找关键路径:挨个数



 浙公网安备 33010602011771号
浙公网安备 33010602011771号