数据结构基础第5讲
数据结构基础第5讲 树和二叉树
本章内容:

考点一:基本术语
1.数的引入
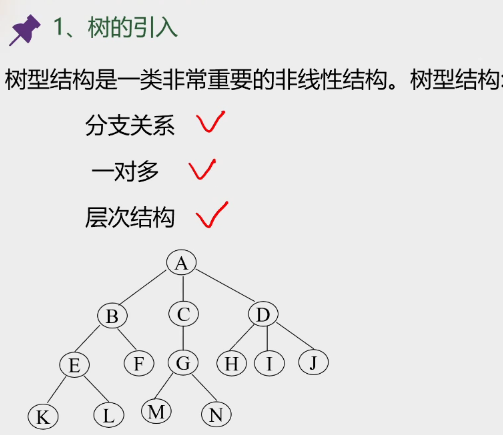
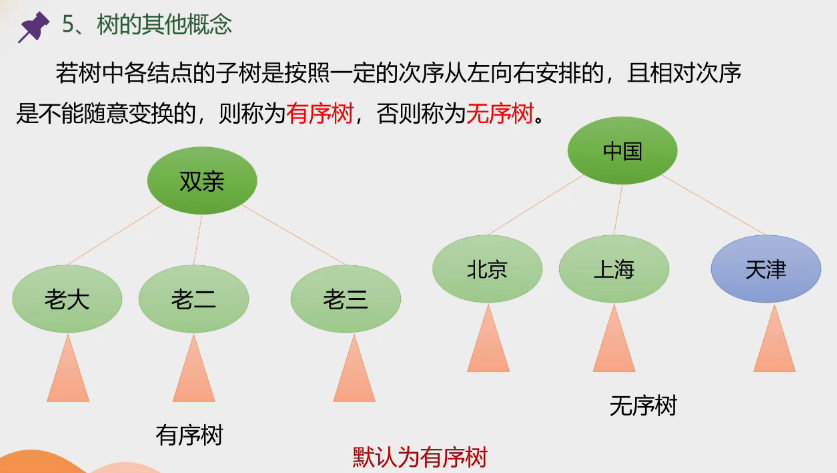
2.树的定义
层次,分支,一对多。
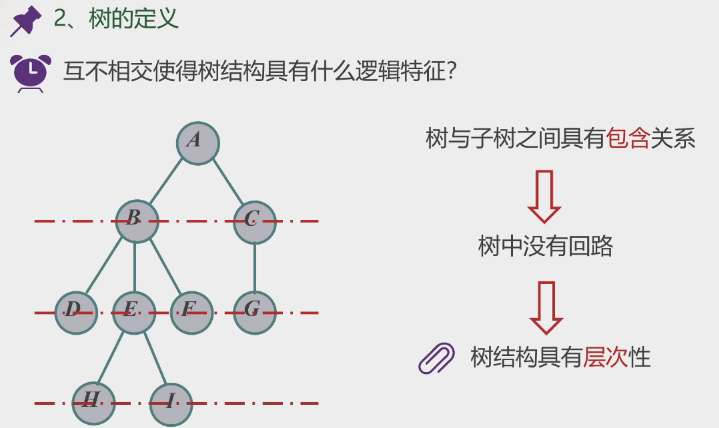
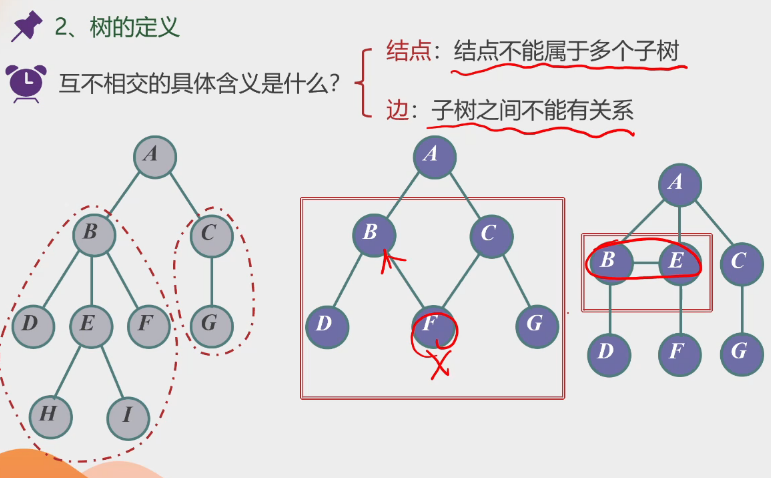
互不相交的含义:
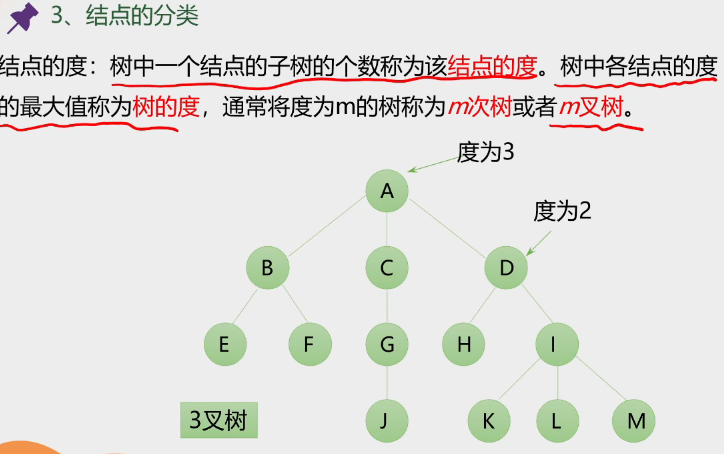
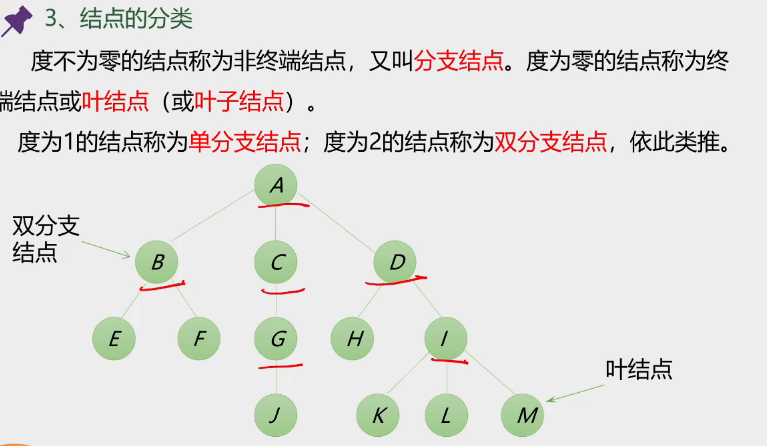
3.结点的分类

-
结点的度:
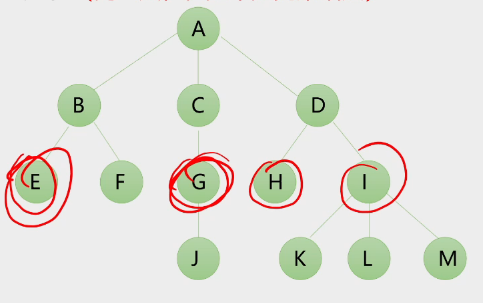
4.结点的关系

-
树的深度:树中结点最大高度称为树的高度(或树的深度)
-
行兄弟结点:在同一层但不是兄弟的结点
-
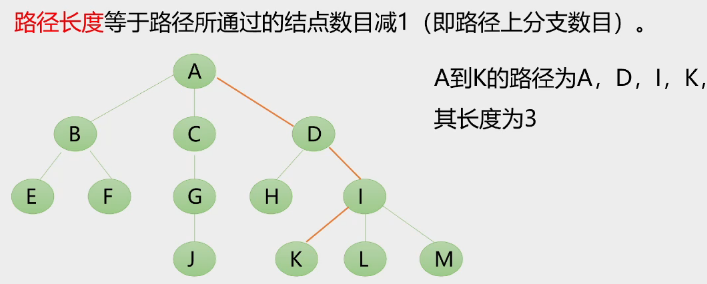
路径长度:等于路径所通过的结点数目减1(即路径上分支数目)
-
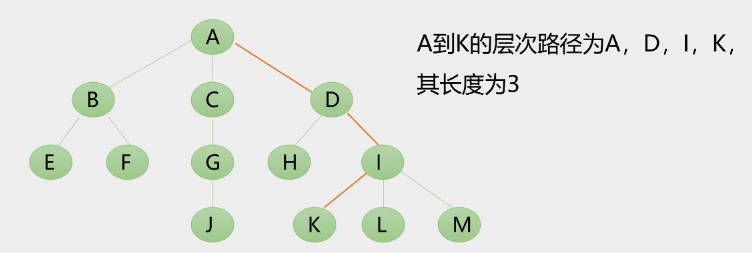
层次路径:从根节点开始,到达某节点p所经过的所有结点成为结点p的参差路径(有且只有一条)
-
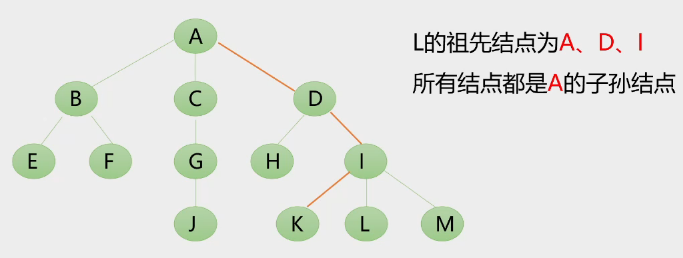
子孙结点:一个结点的所有子树中的结点
-
祖先结点:从根节点到达一个结点的路径上经过的所有结点
5.树的其他概念
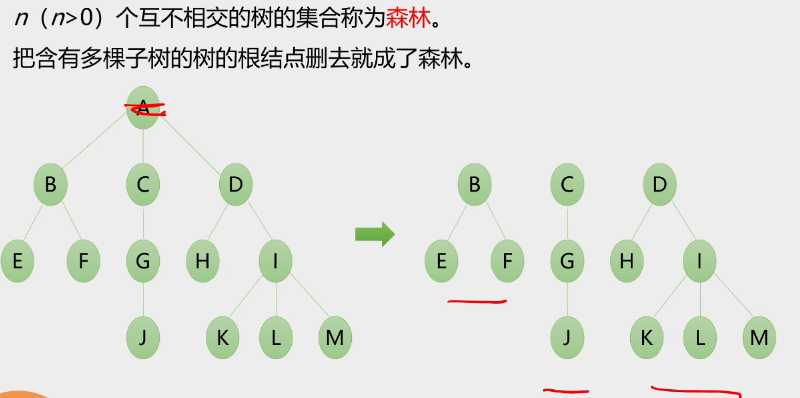
n个互不相交的树的集合叫做森林
考点二:树的性质和存储
1.树的性质
-
性质1:树中所有节点数等于所有结点度数之和+1

-
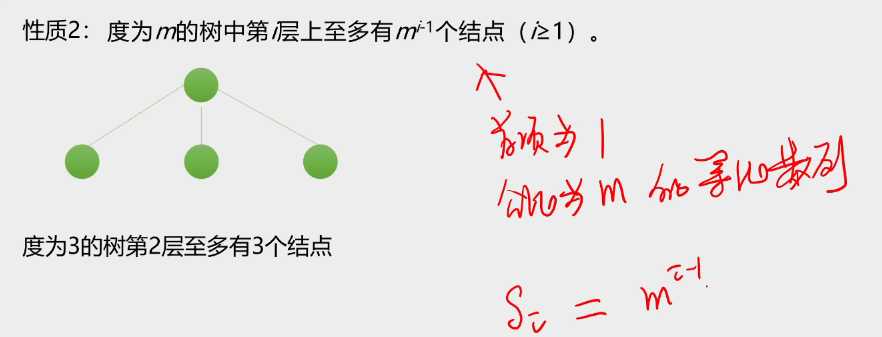
性质2:度为m的树中第i层上至多有\(m_{i-1}\)个结点(\(i \geqslant1\))
-
性质3:高度为h的m次树之多有\(\frac{m^h-1}{m-1}\)个结点。

-
性质4:具有n个结点的m次数的最小高度为\(\lceil \log_m(n(m-1)+1)\rceil\)

-
1.给定h
\[\left \{ \begin{matrix} 每层结点最多 \Rightarrow 总的结点就最多\\ 每层结点最少 \Rightarrow 总的结点最少 \end{matrix} \right . \] -
2.给定n
\[\left \{ \begin{matrix} 每层结点越多 \Rightarrow h越小\\ 每层结点越少 \Rightarrow 高度越少 \end{matrix} \right . \]
-
-
性质5:对于m度树,定义叶子结点个数为\(n_0\),度为1的结点个数为\(n_1 \cdots\),度为m的结点个数为\(n_m\),于是有\(n_0=n_2+2*n_3+3*n_4+\cdots+(m-1)*n_m+1\)

2.树的存储
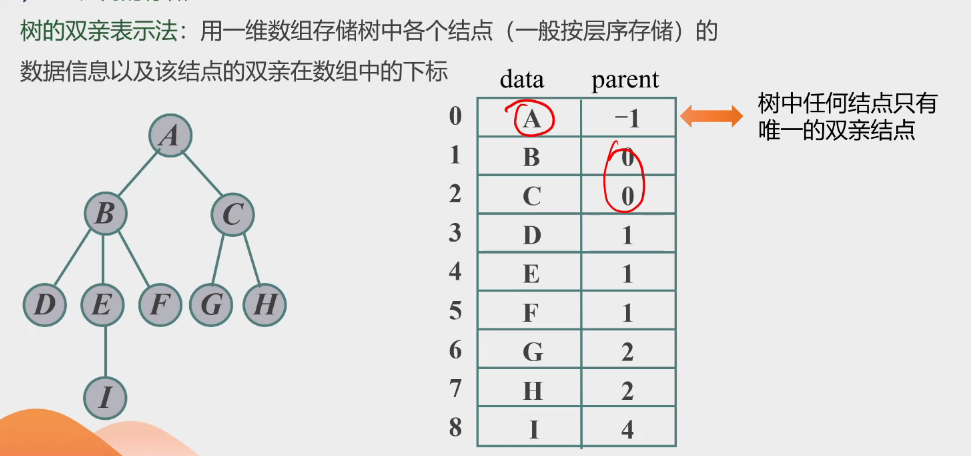
双亲表示法:
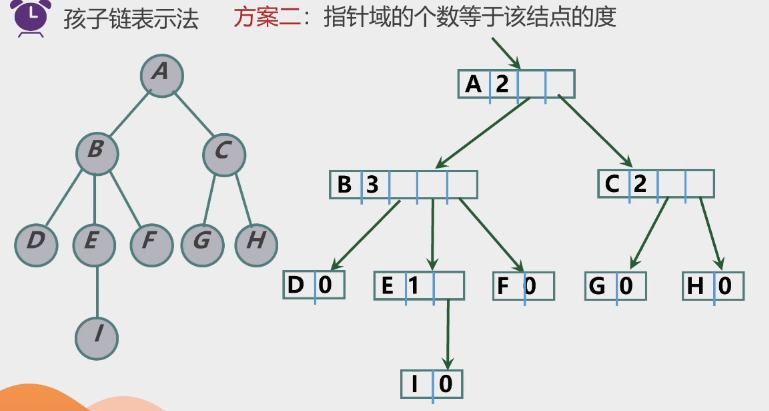
孩子链表示法:
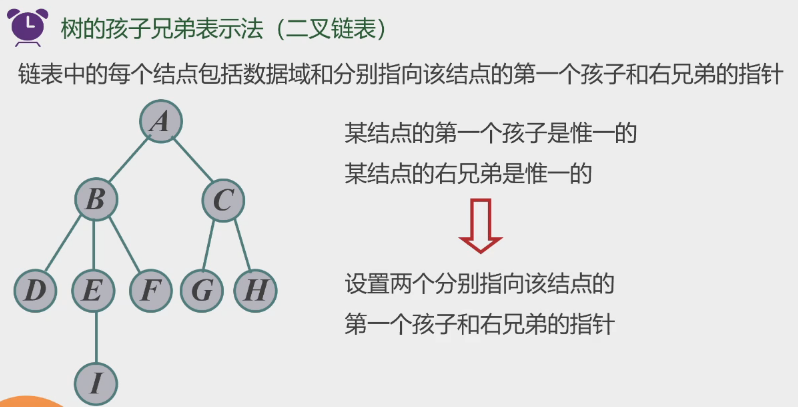
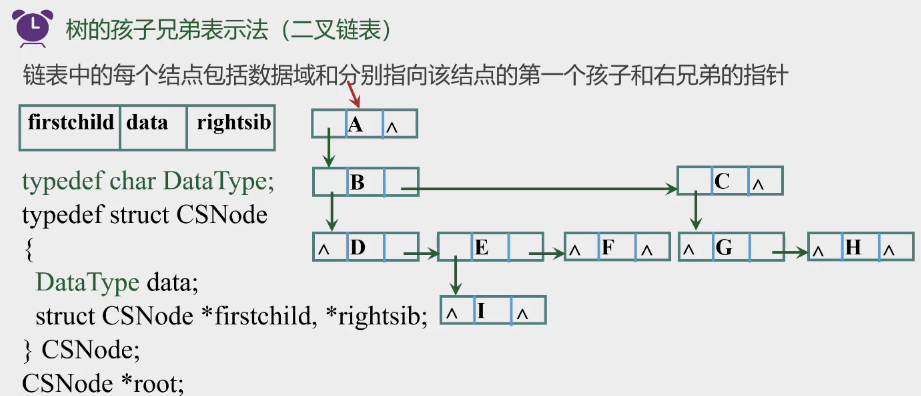
孩子兄弟链:
考点三:二叉树\(\bigstar \bigstar \bigstar \bigstar \bigstar\)
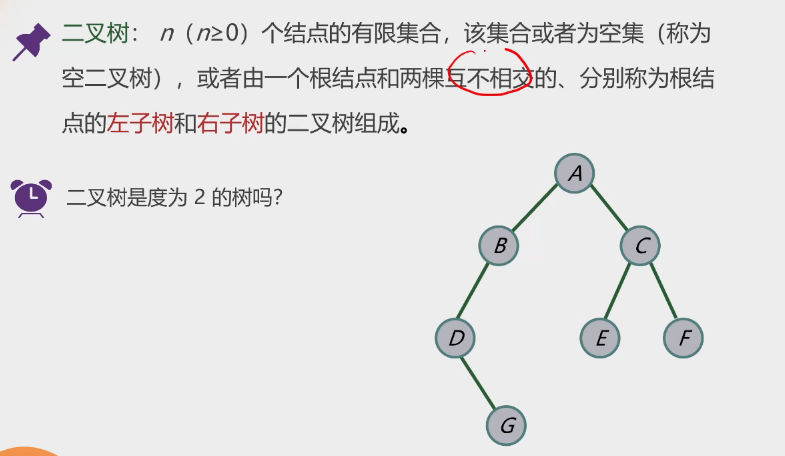
1.二叉树基本形态
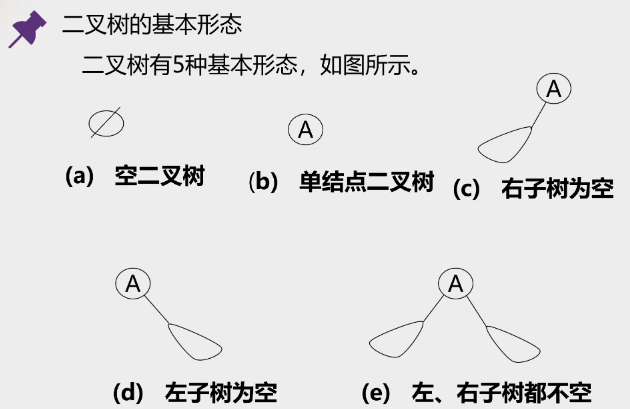
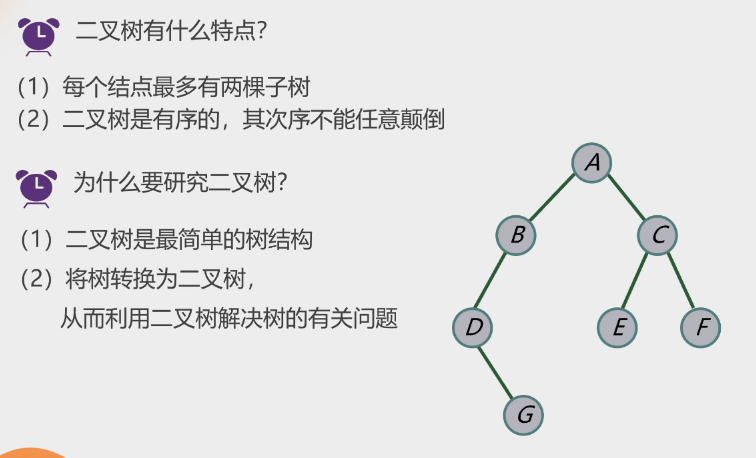
2.二叉树特点:
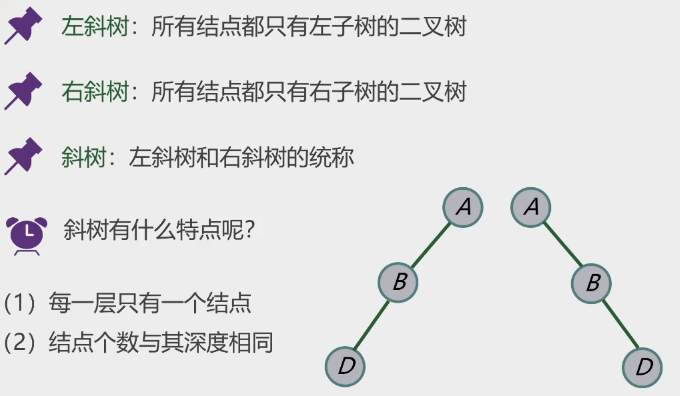
3.左右斜树:
4.性质
-
性质1:在非空二叉树中,第i层上至多有\(2^{i-1}个结点(i \geqq 1)\)

-
性质2:深度为k的二叉树至多有\(2^k-1个结点(k \geqq 1)\)

-
性质3:对任意一棵二叉树,若其叶子结点数为\(n_0\),度为2的结点数为\(n_2\),则\(n_0=n_2+1\)
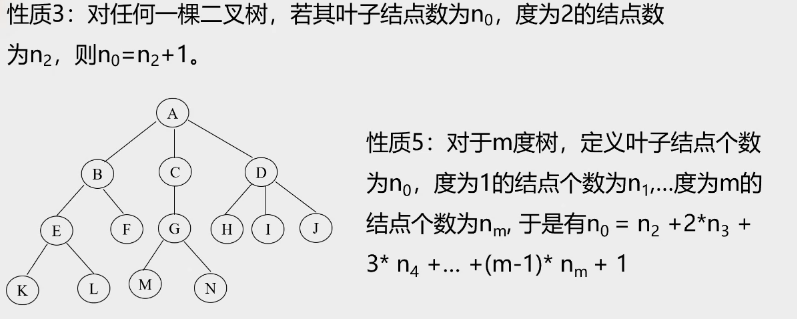
-
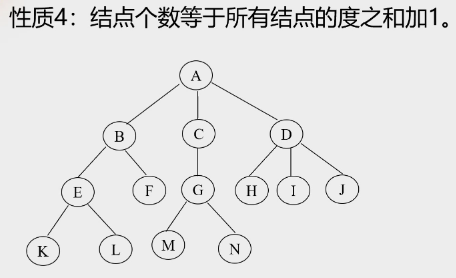
性质4:结点个数等于所有结点的度之和加1
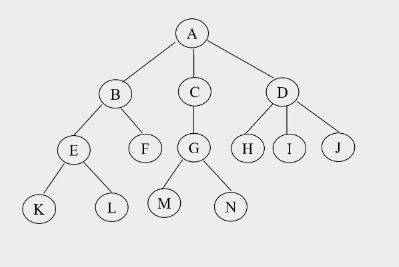
-
性质5:具有n个结点的二叉树的最小高度为\(\lceil \log_2(n+1)\rceil\)
回顾性质2:深度为k的二叉树至多有\(2^k-1\)个结点\(k \geqq 1\).
\(n \leqq 2_k-1;得出k=\lceil \log_2(n+1)\rceil\)
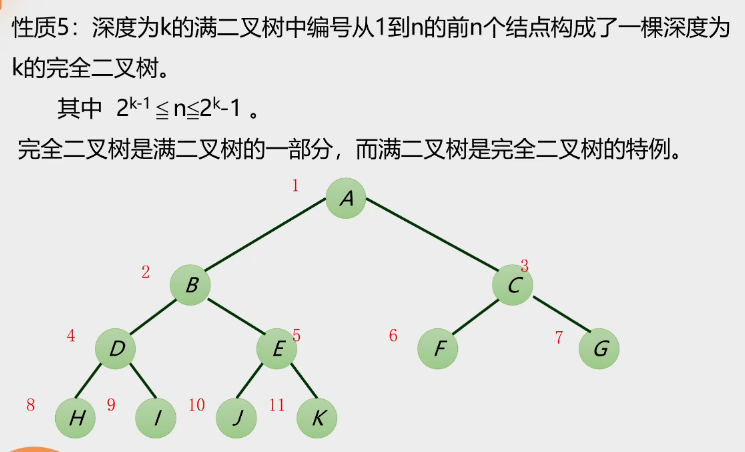
5.完全二叉树和满二叉树
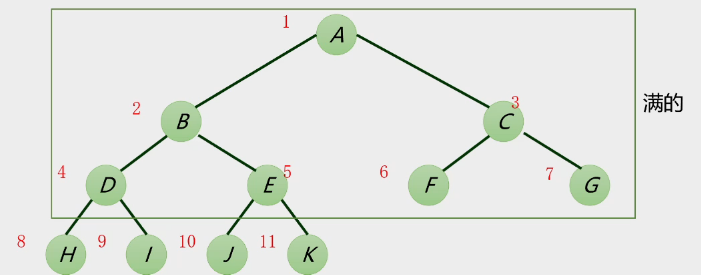
1.满二叉树
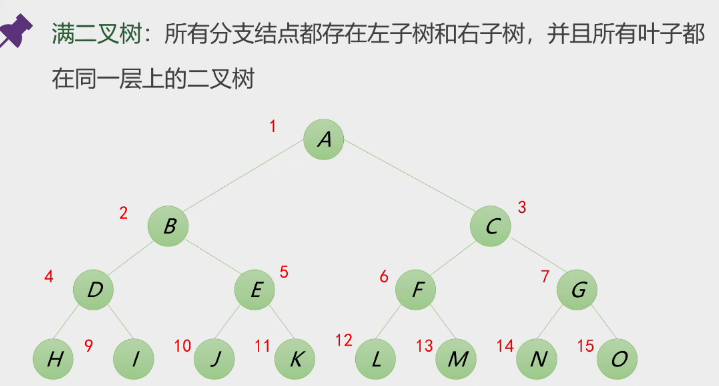
- 特点:
- 叶子只能出现在最下一层
- 只有度为0和度为2的结点
- 在同样深度的二叉树中结点个数最多
- 在同样深度的二叉树中叶子结点个数最多
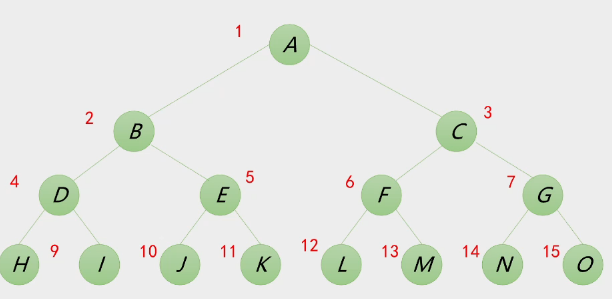
2.完全二叉树
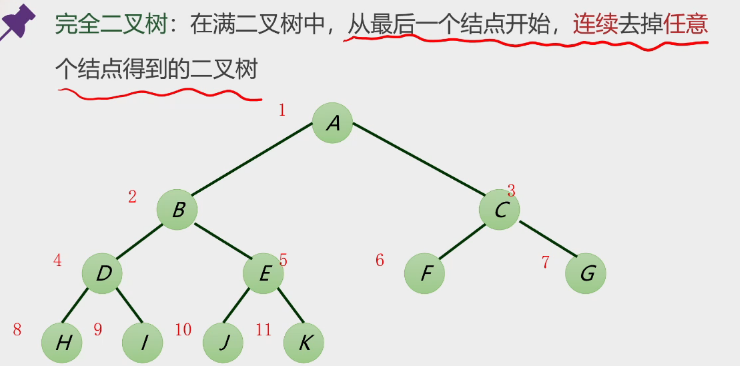
-
特点
-
叶子结点只能出现在最下两层且最下层的叶子结点都要集中在二叉树左面
-
完全二叉树中如果有度为1的结点,只可能有一个,且该节点只有左孩子
-
深度为k的完全二叉树在\(k-1\)层上一定是满二叉树
-
-
完全二叉树性质
-
性质1:在非空二叉树中,第i层上至多有\(2^{i-1}\)个结点\((i \geqq1)\)。

-
性质2:

-
性质3:
\(n_1\)的存在并不改变叶子总数,但改变结点总数

-
性质4:
-
性质5:
-
性质6:

-
性质7:
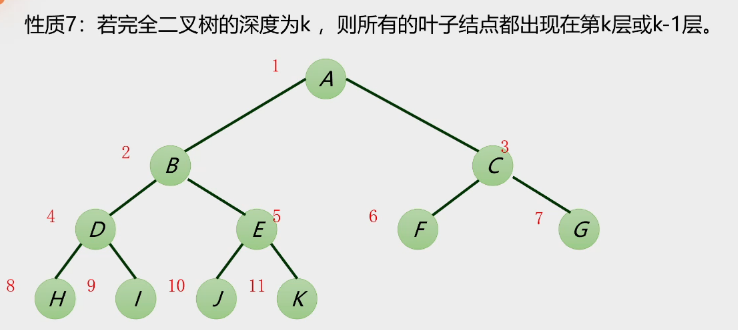
-
性质8:
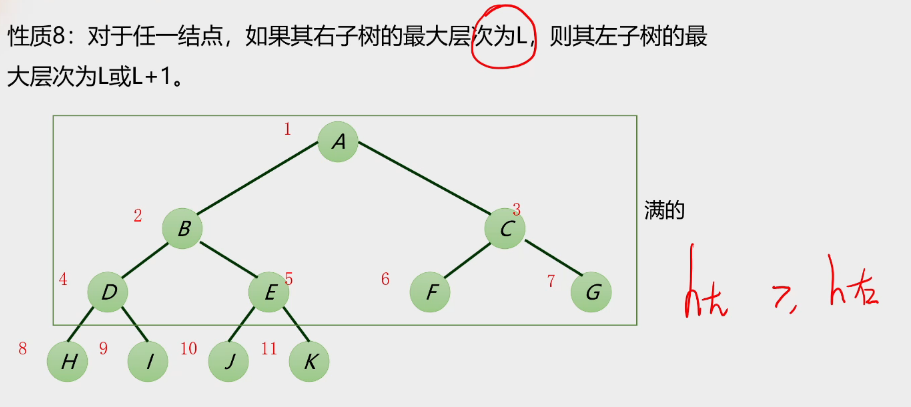
-
性质9:
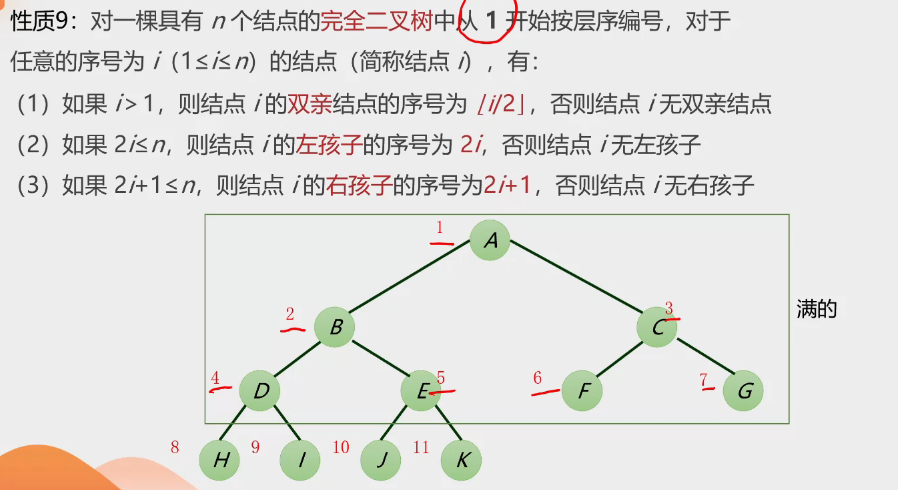
-
性质10:
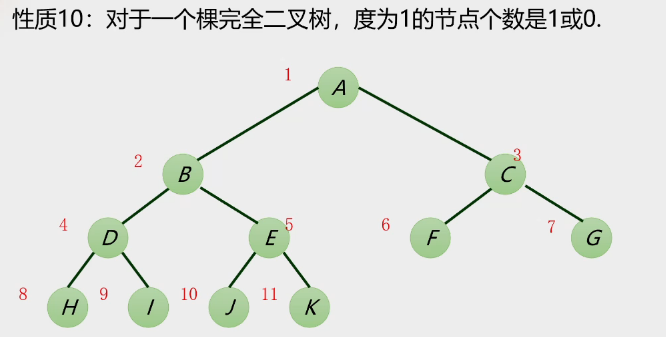
-
点拨
-
完全二叉树叶子结点个数
完全二叉树按顺序排列的,所以最后一个结点的父亲结点是最后一个父结点,后面就全是叶子了。

3.二叉树的存储
-
非完全二叉树的顺序存储结构:
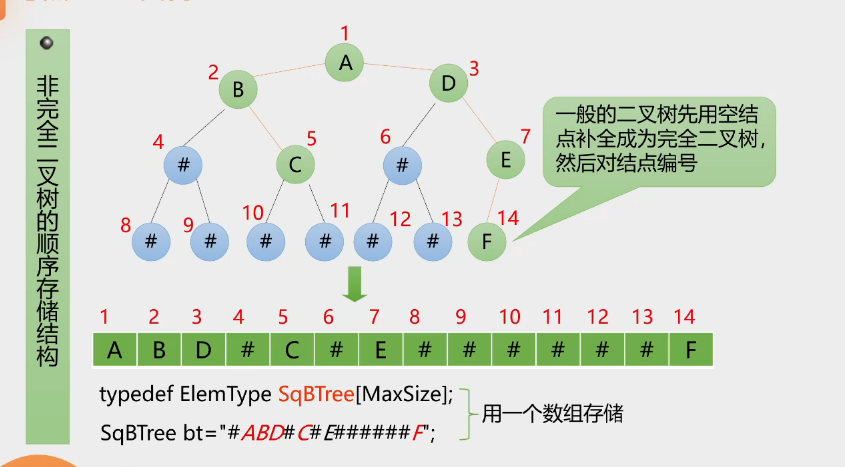
-
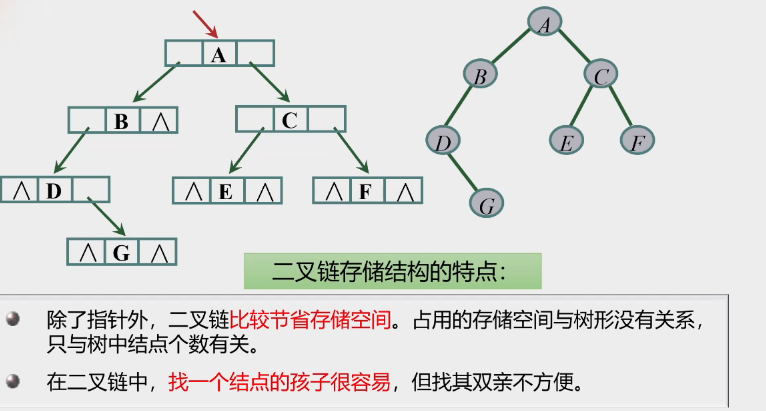
二叉树的存储结构特点:
考点四:二叉树的遍历
1.遍历
-
先序遍历
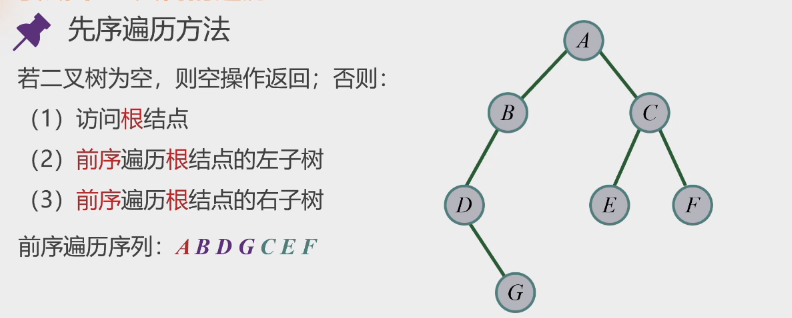
-
中序遍历
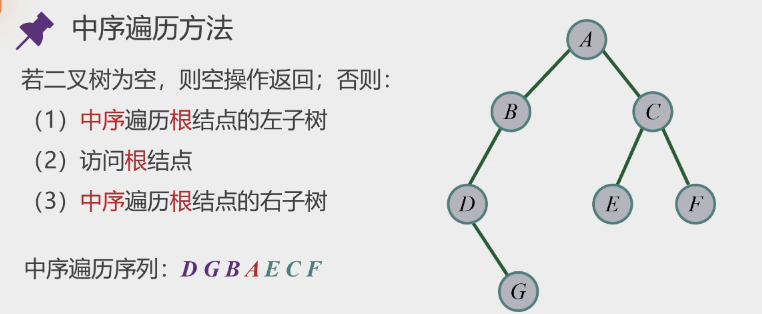
-
后续遍历
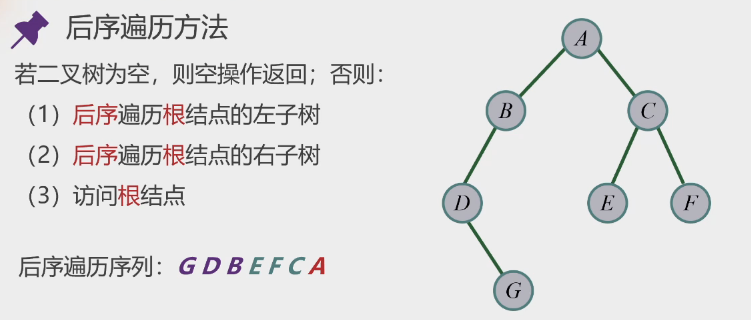
-
层次遍历
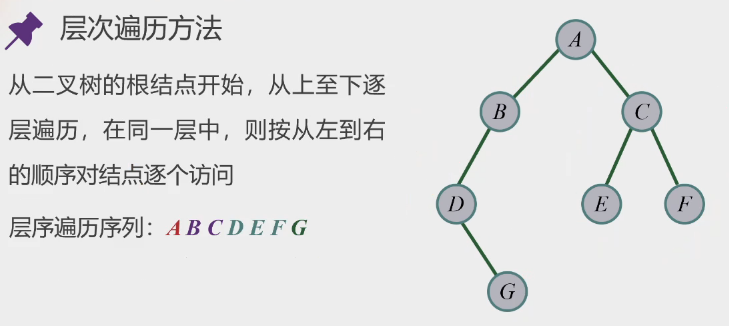
-
遍历题型
- 中序
- BST
- 求语法树找中缀
- 题目规定
- 先序
- 总分结构
- 自顶向下
- 后序
- 分总
- 自底向下
2.二叉树遍历性质

3.二叉树的生成
-
确定根结点及左右子树

-
左子树BC确定
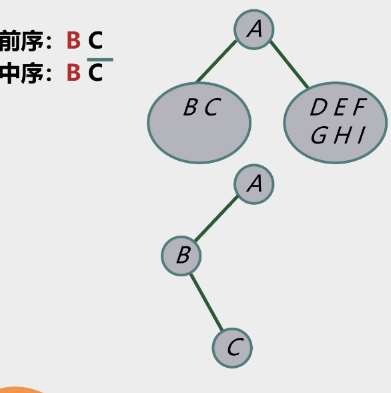
-
右子树确定根结点及其左右子树
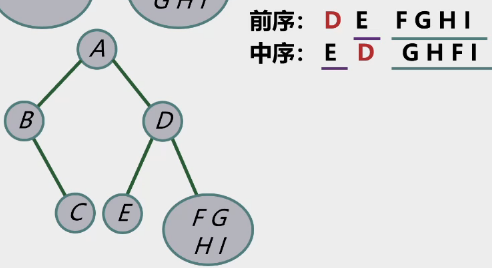
-
在其右子树同
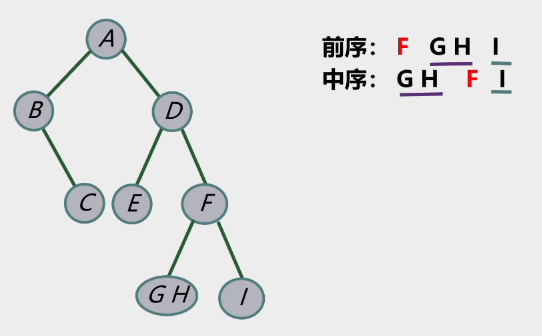
-
最后完成左子树
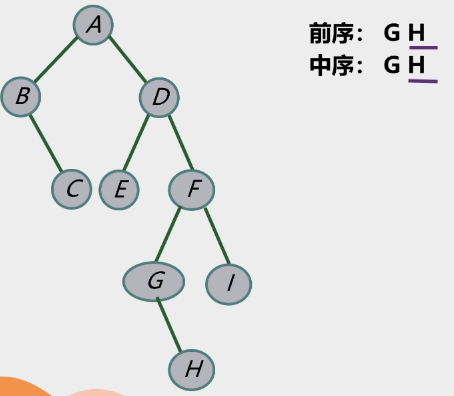
中序作用:确定左子树
先序作用:找到根节点
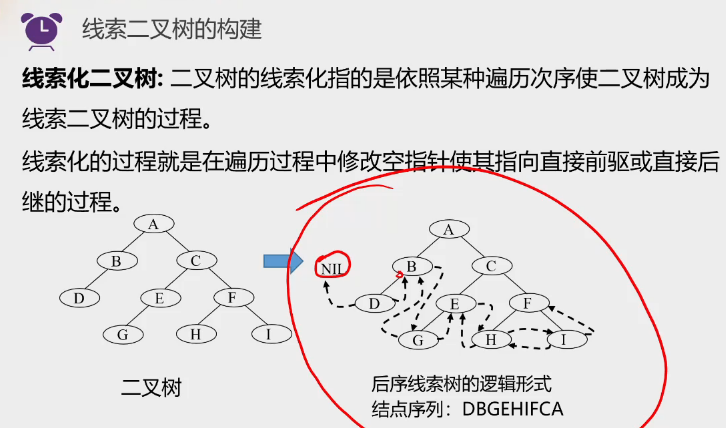
考点五:线索二叉树
1.线索二叉树


2.建立过程
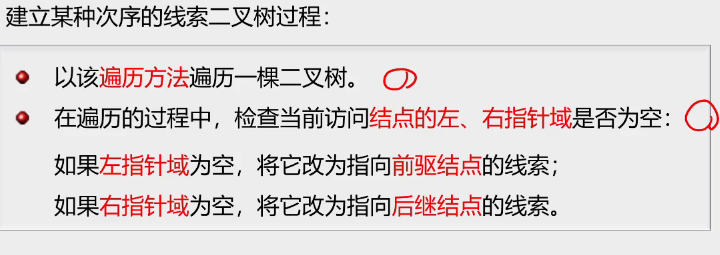
3.线索化过程
考点六:树、森林和二叉树的关系
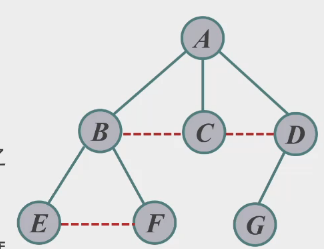
1.树转二叉树

左孩右兄弟
-
兄弟之间连根线
-
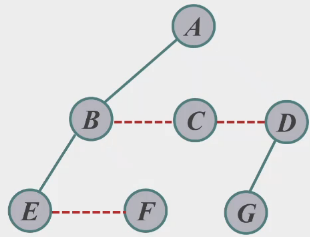
除第一个孩子节点之间的连线,删去其他连线
-
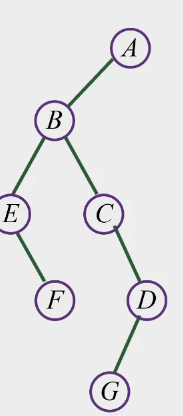
旋转为二叉树
-
先先后中

2.二叉树转树

-
从左孩子右链走,每遇到结点加连线。
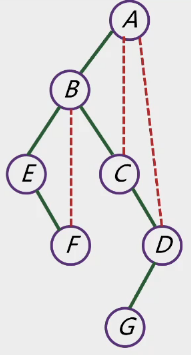
-
删去所有双亲结点与右孩子结点的连线。
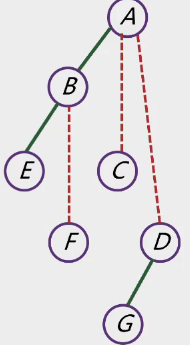
-
层次调整
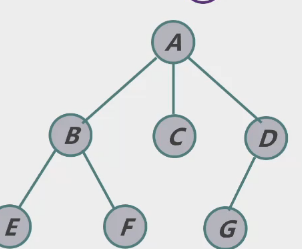
3.森林转二叉树
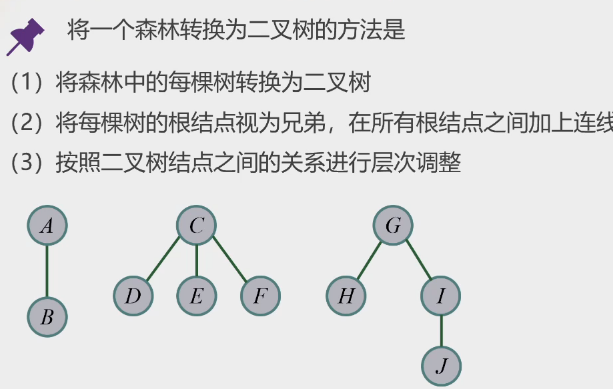
-
把每棵树转换成二叉树
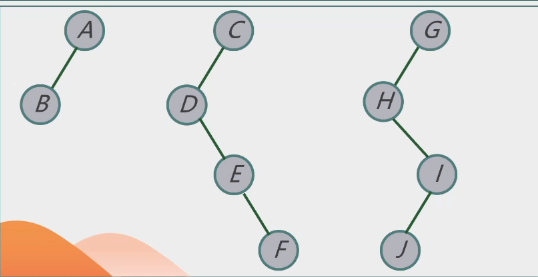
-
根节点视为兄弟,接线
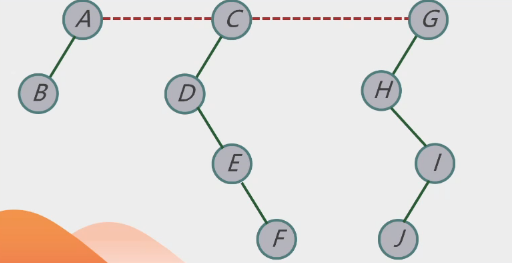
-
层次调整
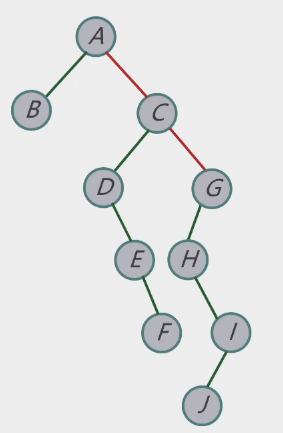
考点七:哈夫曼树
1.基本概念

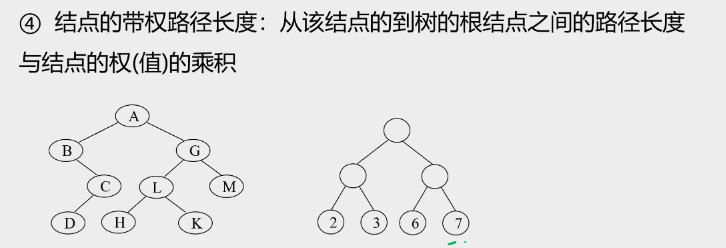


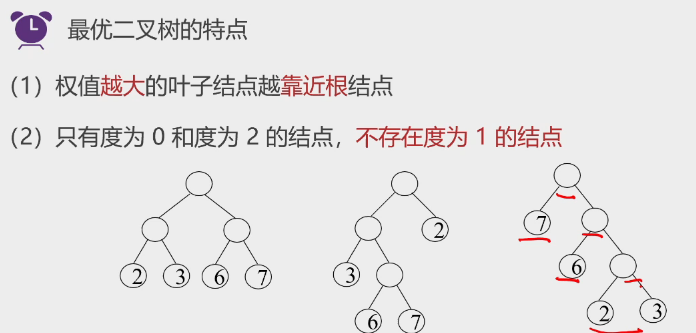
2.最优二叉树的特点
3.构造哈夫曼树的原则

4.构建哈夫曼树过程

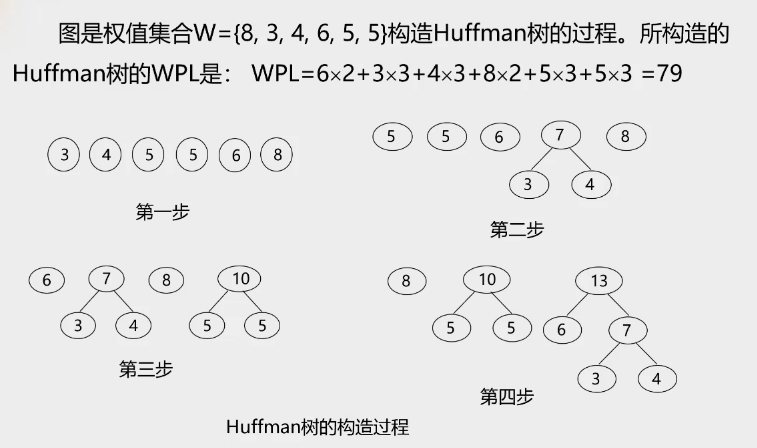
左小右大,左低右高

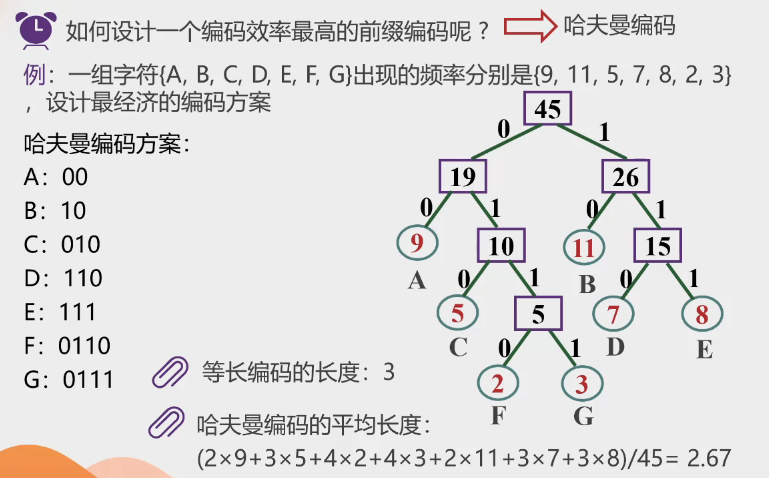
5.哈夫曼编码
-
相互互斥,没有前缀,实现长短不一
-
特点:

考点八:并查集
-
定义

-
操作




 浙公网安备 33010602011771号
浙公网安备 33010602011771号