数据结构基础第3讲
数据结构基础第3讲 栈及其应用
内容

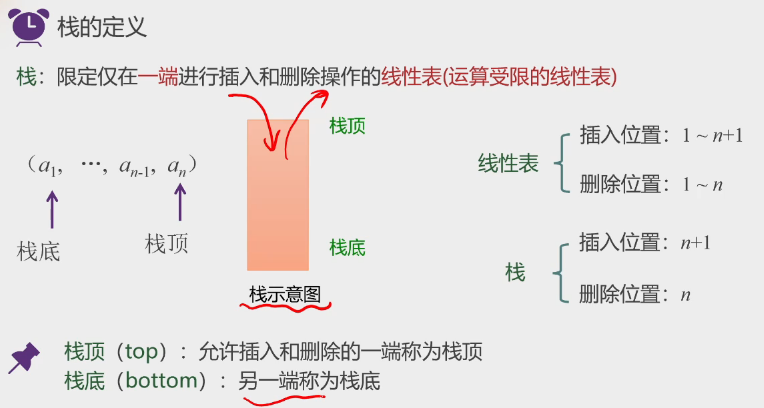
考点一:栈的概念
1.顺序栈的定义:
-
出栈顺序情况计算
给定n个元素,出栈顺序的情形满足卡特兰数,计算公式:
\[\frac{C_{2n}^{n}}{n+1} \]例题:
确定第一个出栈的谁。有两种可能:
找带头大哥。


-
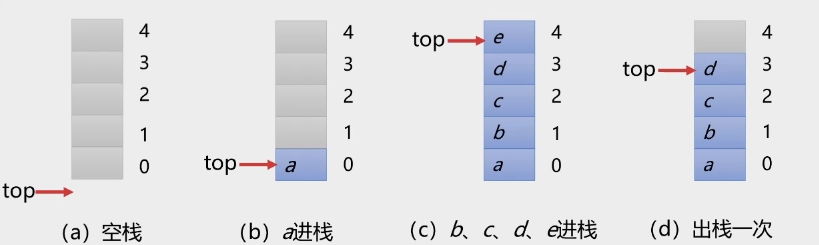
栈的顺序存储结构
顺序栈操作
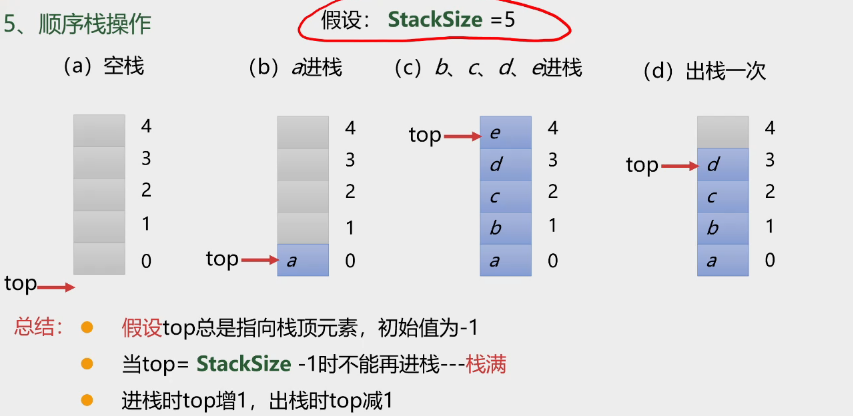
顺序栈4要素
-
栈空条件: top = -1
-
栈满条件: top = StackSzie - 1
-
进栈操作:top++;将e放在top处
-
退栈操作: 从top处取出元素e; top--;
-
-
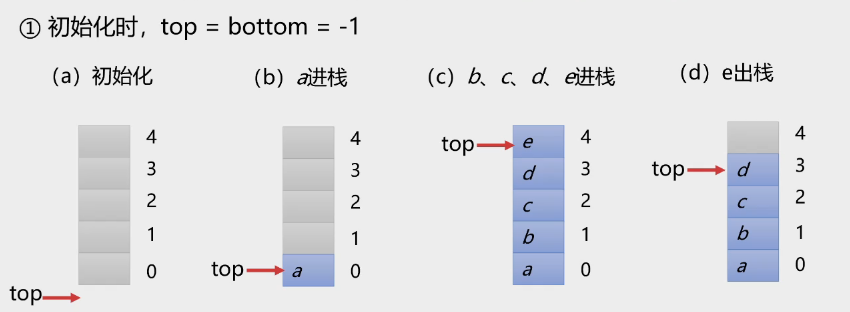
栈的临界条件
-
初始化时,top = bottom = -1
-
入栈:
s -> top++; //栈顶指针+1 s -> data[s -> top] = a; // 元素a放在栈顶指针处top始终指向栈顶元素
bottom指向-1
-
出栈
x = s -> data[s -> top]; s -> top--; // 栈顶指针-1栈中元素个数top+1个
当top+1 >= n时栈满
-
(考试默认情况)初始化时,top = bottom = 0

-
进栈
s -> data[s -> top] = a; // 元素a放在栈顶指针处 s -> top++; // 栈顶指针+1top指向栈顶元素的下一个空位置
bottom指向0
-
出栈
s -> data[s -> top]; // 栈顶指针-1 x = s -> data[s -> top]栈中元素个数top个
top >= n时栈满
-
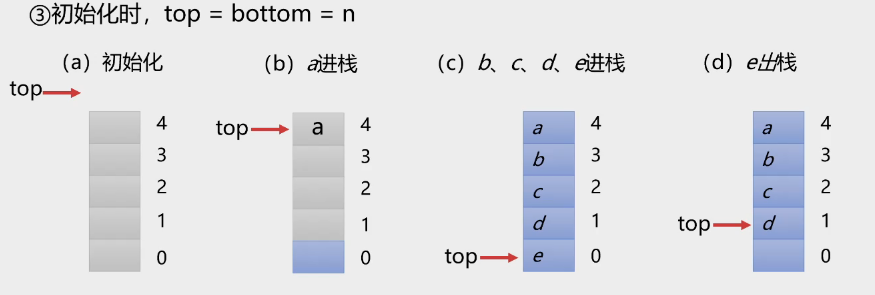
初始化时, top = bottom = n
-
入栈
s -> top--; // 栈顶指针-1 s -> data[s -> top] = a; // 元素a放在栈顶指针处top始终指向栈顶元素
bottom始终指向n
-
出栈
x = s -> data[s -> top]; s -> top++; // 栈顶指针+1元素个数n-top个
当n - top >= n
时栈满
-
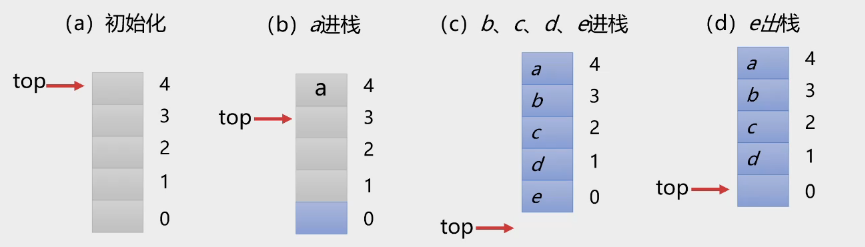
初始化时, top = bottom = n - 1
-
入栈
s -> data[s -> top] = a; // 元素a放在栈顶指针处 s -> top--; //栈顶指针-1top始终指向栈顶元素的下一个空位置
bottom始终指向n - 1
-
出栈
s -> top++; // 栈顶指针+1 x = s -> data[s -> top];元素个数n-top-1个
当n - top-1 >= n
时栈满
-
2.对顶栈(共享栈)
两个栈底位于两端,栈顶往中间聚拢

共享栈的4要素:

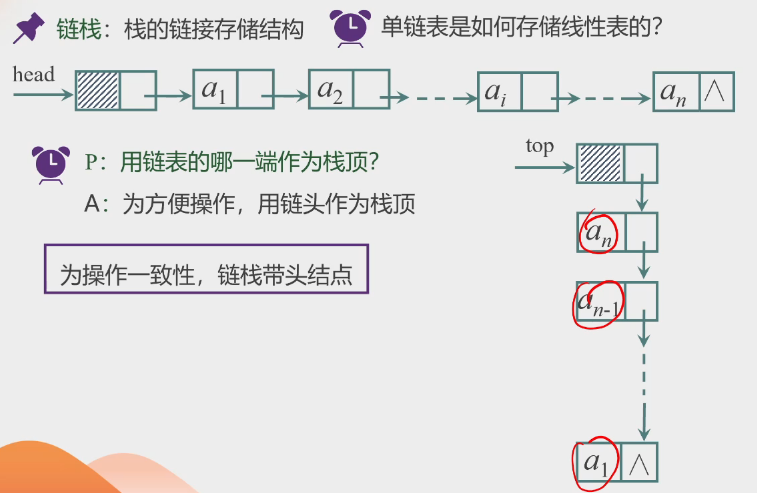
考点三:栈的链式结构
示意图:
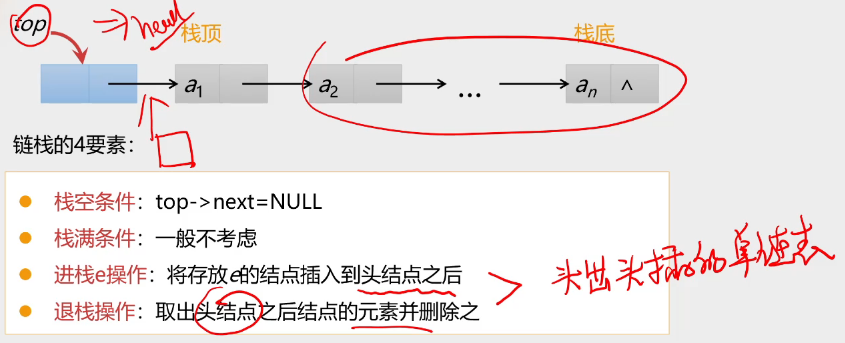
链栈4要素:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号