数据结构基础第1讲

数据结构基础课第1讲

• 4/17

考点一：基本概念

\[数据：能输入到计算机的符号集合 \left \{ \begin{matrix} 数值数据：整数，实数 \\ 非数值数据：图像，声音 \end{matrix} \right . \]

数据对象： 性质相同 的数据元素集合，是数据的子集。

数据元素：数据的基本单位
数据项：构成数据元素的最小的单位

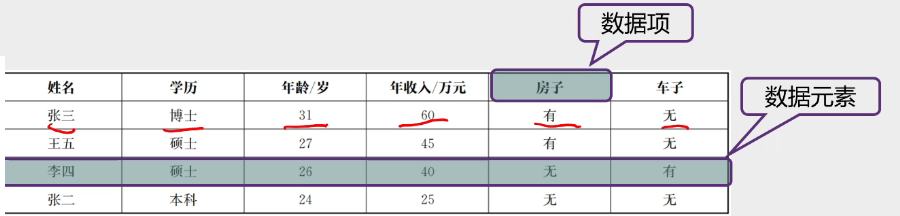
数据结构：数据元素之间存在特定的关系

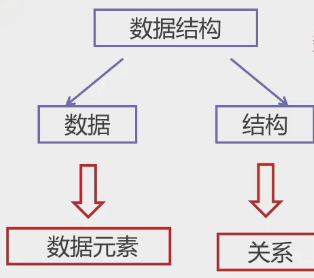
数据的逻辑结构：数据元素之间逻辑关系的整体
（在讲数据结构的时候等价于逻辑结构）

考点二：逻辑结构

逻辑关系：元素与元素之间自然或人为定义的“关系”，相应的结构称为逻辑结构/概念结构

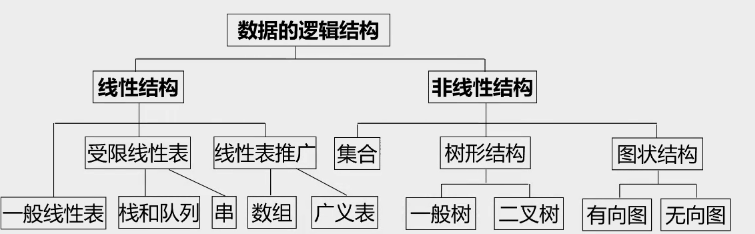
数据结构从逻辑上分为四类：

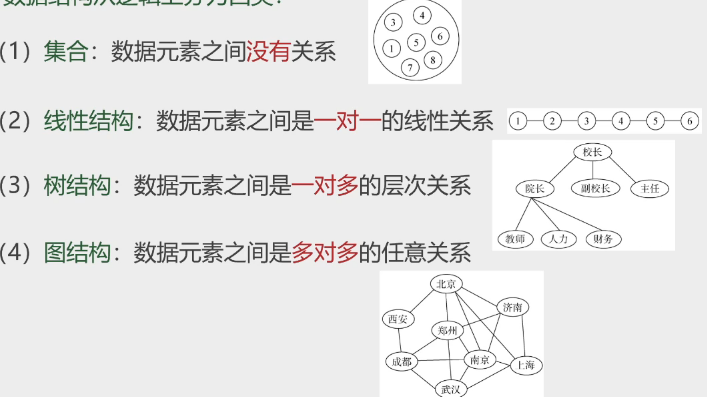
\[逻辑结构：有时直接称为数据结构 \left \{ \begin{matrix} 线性结构：线性表，栈，队列，串\\ 非线性结构：树，图，多维数组，广义表 \end{matrix} \right . \]

说明：

数据类型：值和操作的集合

抽象数据类型（ADT）：指的是从求解问题的数学模型中抽象出来的数据结构和运算（抽象运算）《画饼》

实现依赖具体数据结构

考点三：物理结构

物理结构/存储结构完成的问题——如何把数据放到计算机中进行处理

1.顺序结构

位置关系表示逻辑关系

逻辑上相邻，物理上也相邻

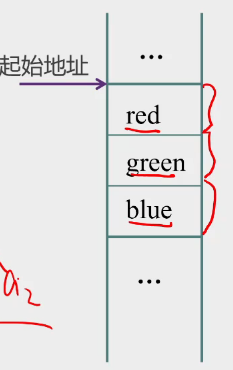
特点：

2.链接存储结构

通过指针表示逻辑关系

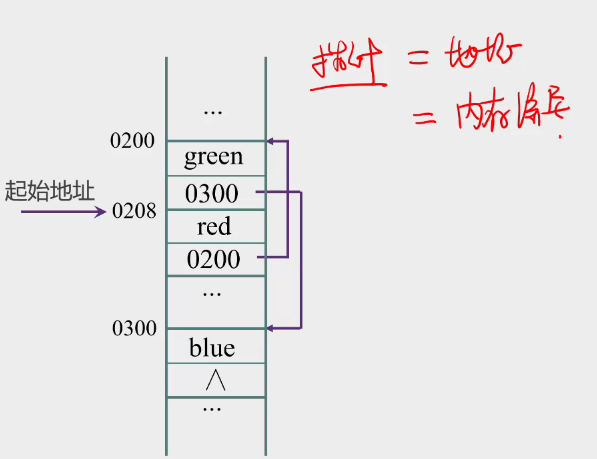
特点：
存储密度小

3.索引结构

数据元素之间无关系，索引之间存在关系，先有数据再有索引。

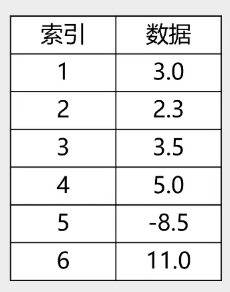
特点：

4.散列结构

在存储位置与关键代码之间建立确定关系的查找技术。

逻辑结构与存储结构的关系

数据结构

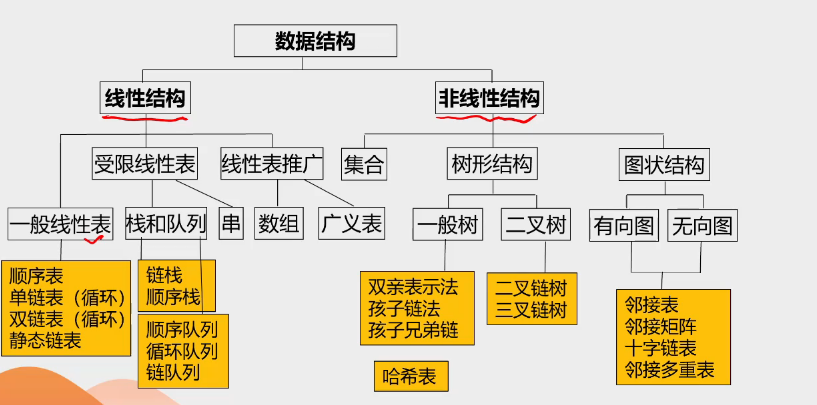
考点四：算法的概念和评价

重要特性：

考点五：时间复杂度(\(\bigstar \bigstar \bigstar \bigstar \bigstar\))

\[统计方法\left \{ \begin{matrix} 事后统计：计算机内部执行时间和实际占用空间统计。 \\ 事前分析：求出该算法的一个时间界限函数。\end{matrix} \right . \]

分析因素：

问题规模 \(n\) 的函数 \(T(n)\) ：算法所有原操作的执行次数

算法执行时间 = 原操作所需时间\(\times T(n)\)

一个例子：

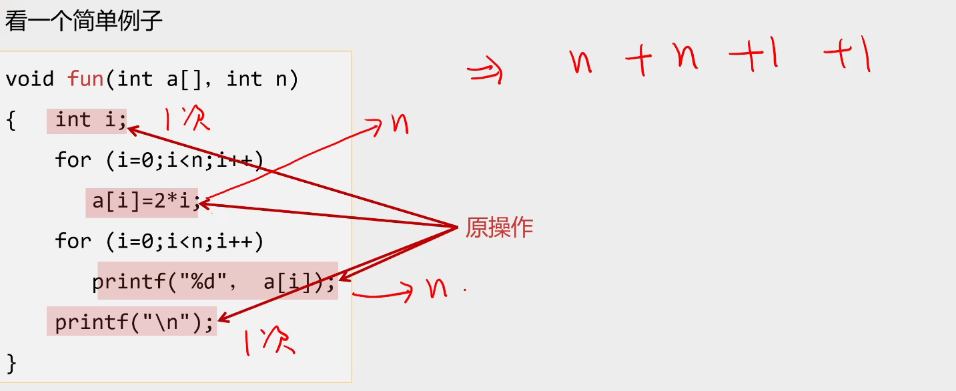
\[注意\left \{ \begin{matrix} 1.n \rightarrow \infty \\2. 忽略系数 \\ 3. 忽略低阶 \end{matrix} \right . \]

常量阶：与问题规模\(n\)无关

线行阶：

平方阶：

总结：

\[单重循环: i=1 \stackrel{i=i+1}{\rightarrow} n \qquad O(n) \]

\[双重循环:\left \{ \begin{matrix}&1.内外无关 O(m \times n) \qquad m:外层次数; n:内层次数 \\ &2.内外无关：做累加和 \end{matrix} \right . \]

三次方阶例子：

时间复杂度 \(\log_a n\) 指数\(a\)可以忽略掉

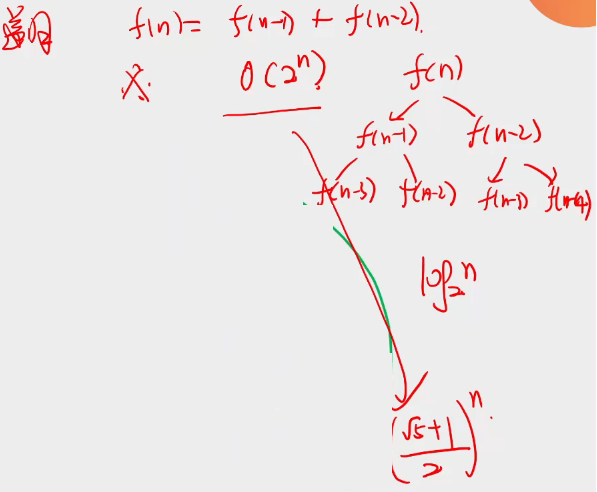
递归

从初始条件出发，沿着转移条件抵达终止条件。

例子：
O(n)

\[\divideontimes 递归\left \{ \begin{matrix} \left . \begin{matrix} 1.\qquad n \stackrel{n=n-1}{\rightarrow} 1 \\2. \qquad n \stackrel{n=n+1}{\rightarrow} n \end{matrix} \right . \qquad \qquad &情况1，2：O(n)\\ \left . \begin{matrix} 3.\qquad n \stackrel{n=n/k}{\rightarrow} 1 \\ 4.\qquad 1 \stackrel{n=n \times k}{\rightarrow} n \end{matrix} \right . \qquad &情况3，4：O(\log_k n)\end{matrix} \right . \]

1. 情况5：O(2^n)
   

2. 情况6：\(O(n^\frac{1}{2})\)
   

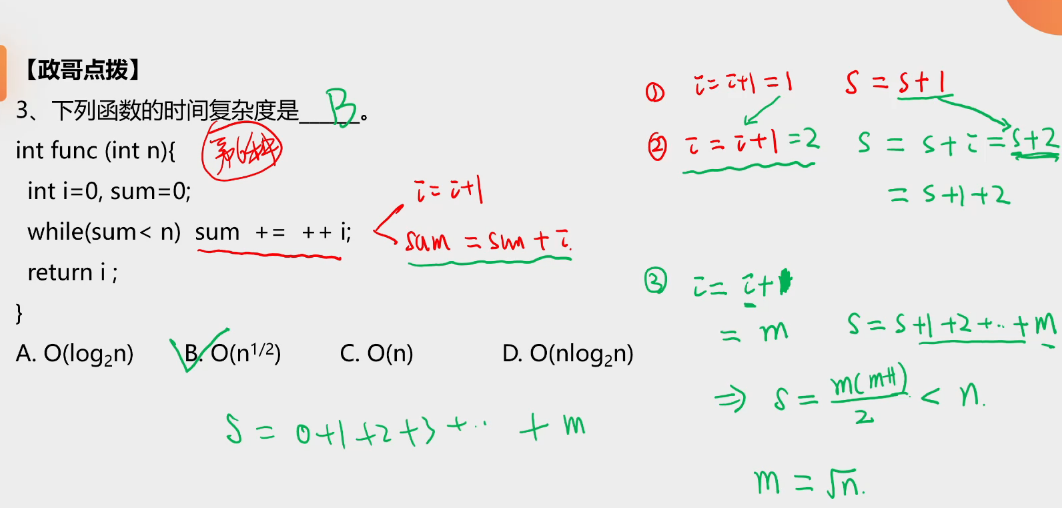
3. 情况7：\(O(n \times \log_2 n)\)
   

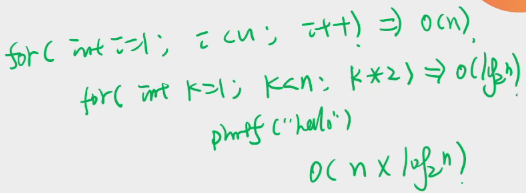
4. 情况8：\(O(n)\)

   for(int i = 1; i < n; i * 2) # log_2 n项
       for(int j = 0; j < i; j++)
           printf("hello");     # O(n)
   

\[\log_2 n \left \{ \begin{align} i&=1 \qquad j=0 \qquad \qquad &1次\\ i&=2 \qquad j=0,1 \qquad &2次 \\ i&=n \qquad j=0,1,2 \cdots n-1 \qquad &n次 \end{align} \right . \]

\[1+2+4+ \cdots + n \Rightarrow S_n = \frac{1(1-2^{\log_2 n})}{1-2} = \frac{1\times (1-2^k)}{1-2}=n-1 \qquad k = \log_2 n \]

考点六：空间复杂度分析

只关心零时变量
例子：