代码随想录第十八天 | Leecode 530. 二叉搜索树的最小绝对差、501. 二叉搜索树中的众数、236. 二叉树的最近公共祖先

530. 二叉搜索树的最小绝对差

题目描述

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

• 示例 1：

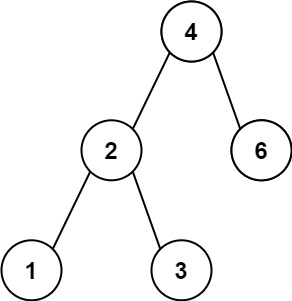
输入：root = [4,2,6,1,3]
输出：1

• 示例 2：

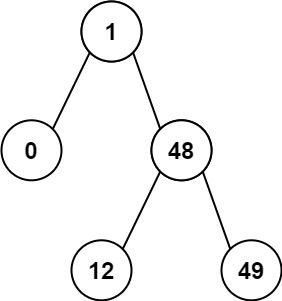
输入：root = [1,0,48,null,null,12,49]
输出：1

解法1 中序遍历递归求解

class Solution {
public:
    void inOrder(TreeNode* root, vector<int>& inOrderVec, int& minAbs){
        if(!root) return;
        inOrder(root->left, inOrderVec, minAbs);
        if(!inOrderVec.empty()){
            int curAbs = root->val - inOrderVec[inOrderVec.size()-1];
            if(curAbs < minAbs) minAbs = curAbs;
        }
        inOrderVec.push_back(root->val);
        inOrder(root->right, inOrderVec, minAbs);
        return;
    }

    int getMinimumDifference(TreeNode* root) {
        vector<int> inOrderVec;
        int result = 100000;
        inOrder(root, inOrderVec, result);
        return result;
    }
};

Leecode 501. 二叉搜索树中的众数

题目描述

给你一个含重复值的二叉搜索树（BST）的根节点 `root· ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

• 示例 1：

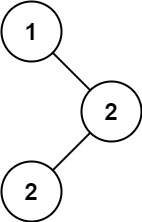
输入：root = [1,null,2,2]
输出：[2]

• 示例 2：

输入：root = [0]
输出：[0]

解法1 暴力搜索

首先看到二叉搜索树，就要立刻想到二叉搜索树的中序遍历就是有序数组。而本题只要拿到中序遍历序列之后，只需要求出序列中出现次数最多的多个值即可。故可将本题拆分为以下几个步骤：

• 先求出中序遍历有序数组
• 遍历数组记录每个值的出现次数，同时记录下其中的最大值（即为众数出现的次数）
• 在根据记录的结果中查看，出现次数最大的都有哪些节点

可以得到代码如下：

class Solution {
public:
    void inOrder(TreeNode* curNode, vector<int>& ordVec){ // 求中序遍历
        if(!curNode) return;
        inOrder(curNode->left, ordVec);
        ordVec.push_back(curNode->val);
        inOrder(curNode->right, ordVec);
        return;
    }


    vector<int> findMode(TreeNode* root) {
        vector<int> inOrderVec;
        inOrder(root, inOrderVec); // 求中序遍历
        unordered_map<int,int> umap; // 建立哈希表
        int maxCount = 0; 
        for(auto val: inOrderVec){ // 用哈希表来记录每个节点出现次数，同时记录出现最大次数
            umap[val]++;
            if(umap[val] > maxCount) maxCount = umap[val];
        }
        vector<int> result;
        for(auto i : umap){ // 再将所有众数都存放到结果中
            if(i.second == maxCount) result.push_back(i.first);
        }
        return result;
    }
};

Leecode 236. 二叉树的最近公共祖先

题目描述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

• 示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1

• 输出：3

解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

• 示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出：5`
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

• 示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

解法1 先求路径再求公共祖先

由于要求的是最深的祖先节点，本题应当是要自下而上的去查找，故应当考虑使用回溯的方法。而之前又做过一道利用回溯来求每个叶节点路径的题目，而本题也可以先求出两个目标节点的路径，再比较两个节点路径中最后一个相等的值，即为要找到公共祖先。根据这个思路可以得到代码如下：

class Solution {
public:
    void findPath(TreeNode* curNode, TreeNode* targetNode, vector<TreeNode*>& curPath, vector<TreeNode*>& resultPath){
        if(!curNode) return;
        curPath.push_back(curNode);
        if(curNode == targetNode){
            resultPath = curPath;
            return;
        }
        findPath(curNode->left, targetNode, curPath, resultPath);
        findPath(curNode->right, targetNode, curPath, resultPath);
        curPath.pop_back(); // 回溯，移除当前节点
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        vector<TreeNode*> tmpPath1, tmpPath2, pPath, qPath;
        findPath(root, p, tmpPath1, pPath);
        findPath(root, q, tmpPath2, qPath);
        int size = min(pPath.size(), qPath.size());
        TreeNode* result;
        for(int i = 0; i < size; i++){
            if(pPath[i] == qPath[i]) result = pPath[i];
            else break;
        }
        return result;
    }
};

今日总结

今天得先去写一下课内计网的作业，因此这三道题的其他解法暂时就不写下来了，之后再来补上。

今日Leecode进度已到67题