代码随想录第十六天 | Leecode 513. 找树左下角的值、112. 路径总和、113. 路径总和 II、106. 从中序与后序遍历序列构造二叉树

Leecode 513. 找树左下角的值

题目描述

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

• 示例 1:

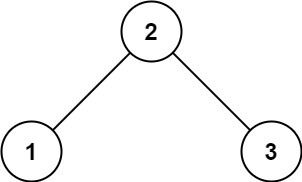
输入: root = [2,1,3]
输出: 1

• 示例 2:

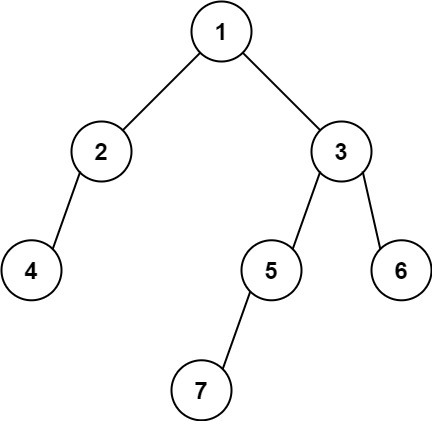
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

迭代法

本题要求最后一层的最左侧节点，那么非常适合采用层序遍历的范式，到最后一层的第一个节点就是要找的数。但由于从上往下层序遍历的时候，并不知道当前层是否是最后一层，因此我们考虑使用一个vector来记录每一层的第一个节点。在遍历结束之后，再从这个vector中取出最后一个数，即为我们要找的最后一层的第一个节点。因此可以有代码如下：

class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        if(!root) return 0;
        queue<TreeNode*> nodeQue;
        nodeQue.push(root);
        vector<int> firstVal; // 用于存放每一层最左侧的值
        while(!nodeQue.empty()){
            int size = nodeQue.size();
            firstVal.push_back(nodeQue.front()->val); // 将当前层第一个节点的值放入firstVal中
            for(int i = 0; i < size; i++){
                TreeNode* cur = nodeQue.front();
                nodeQue.pop();
                if(cur->left) nodeQue.push(cur->left);
                if(cur->right) nodeQue.push(cur->right);
            }
        }
        return firstVal[firstVal.size()-1]; // 最后返回最后一层的第一个节点的值
    }
};

对于层序遍历的标准模板应该都很熟悉了，本题的时间复杂度同样也是\(O(n)\)（即每个节点遍历一次），空间复杂度为\(O(\log n)\)（额外的一个vector大小与二叉树深度相等）。

Leecode 112. 路径总和

题目描述

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

• 示例 1：

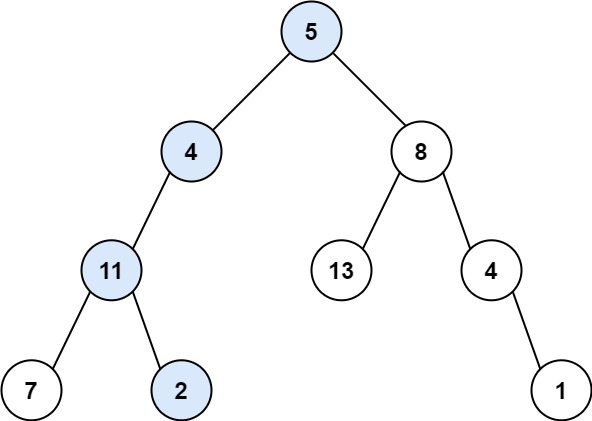
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

• 示例 2：

输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

• 示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

回溯法递归

本题和之前那道求所有路径的题目非常相似，同样也是只要将到达每个节点所经历的路径都记录下来，如果走到叶节点，则将当前路径和进行存放，最后再遍历检查一遍存放的路径和中是否存在有等于目标值的情况，如果有则返回true，否则返回false。根据这个思路可以得到如下代码：

class Solution {
public:
    void pathSumHelper(TreeNode* curNode, vector<int>& pathSum, vector<TreeNode*> ndVec){ // 参数表示：当前节点、存放所有路径和的vec、存放到达当前节点的路径
        if(!curNode) return; // 如果当前节点为空，则直接返回
        ndVec.push_back(curNode); // 否则将当前节点纳入路径中
        if(!curNode->left && !curNode->right){ // 如果当前节点为叶节点，则计算路径和，并存放
            int curSum = 0; // 初始化路径和
            for(int i = 0; i < ndVec.size(); i++){ // for循环遍历路径，求路径和
                curSum += ndVec[i]->val;
            }
            pathSum.push_back(curSum); // 将路径和进行存放
        }
        if(curNode->left) pathSumHelper(curNode->left, pathSum, ndVec); // 递归回溯左子节点，回溯体现在其中的值传递
        if(curNode->right) pathSumHelper(curNode->right, pathSum, ndVec); // 递归回溯右子节点
        return;
    }


    bool hasPathSum(TreeNode* root, int targetSum) {
        vector<int> pathSum;  // 用于存放所有路径和的vec 
        vector<TreeNode*> ndVec; // 用于存放当前路径中经过的所有节点
        pathSumHelper(root, pathSum, ndVec); // 递归调用赋值函数，将所有路径和存放在pathSum中
        for(int i = 0; i < pathSum.size(); i++){ // 遍历pathSum，检查是否有和目标值相等的值
            if(targetSum == pathSum[i]) return true; // 
        }
        return false;
    }
};

同样也可以直接传入一个布尔变量和原本的目标值，在计算完路径和后直接进行比较并修改布尔遍历。这样不必使用一个vector来存放路径和，一定程度上降低空间复杂度：

class Solution {
public:
    void pathSumHelper(TreeNode* curNode,  vector<TreeNode*> ndVec, bool& result, int targetSum){ // 传入布尔变量和目标值
        if(result || !curNode) return; // 如果已经找到，或者当前节点为空，都要返回
        ndVec.push_back(curNode); 
        if(!curNode->left && !curNode->right){
            int curSum = 0;
            for(int i = 0; i < ndVec.size(); i++){
                curSum += ndVec[i]->val;
            }
            if(curSum == targetSum){ // 计算完路径和后直接与目标值比较，如果相等的话就将result变为true并返回
                result = true;
                return;
            }
        }
        if(curNode->left) pathSumHelper(curNode->left, ndVec, result, targetSum);
        if(curNode->right) pathSumHelper(curNode->right, ndVec, result, targetSum);
        return;
    }


    bool hasPathSum(TreeNode* root, int targetSum) {
        vector<int> pathSum;
        vector<TreeNode*> ndVec;
        bool result = false; // 初始没有找到，设置为false
        pathSumHelper(root,  ndVec, result, targetSum); // 递归调用 
        return result;
    }
};

Leecode 113. 路径总和 II

题目描述

给你二叉树的根节点 root 和一个整数目标和 targetSum` ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

• 示例 1：

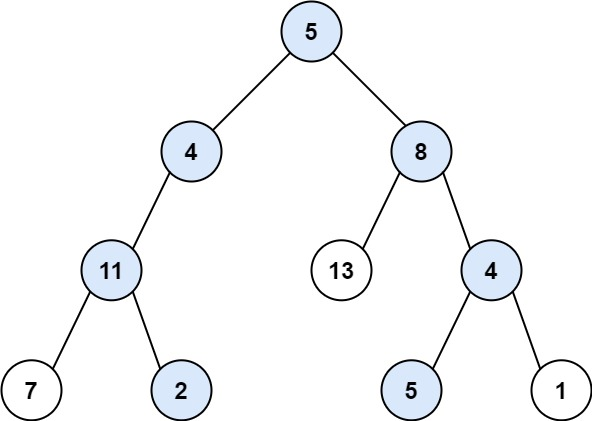
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

• 示例 2：

输入：root = [1,2,3], targetSum = 5
输出：[]

• 示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

回溯递归

和上一题非常类似的方法，区别仅在于需要用一个vector来存放路径。

class Solution {
public:
    void pathSumHelper(TreeNode* curNode, vector<vector<int>>& result, vector<TreeNode*> ndVec, int targetSum){
        if(!curNode) return;
        ndVec.push_back(curNode);
        if(!curNode->left && !curNode->right) {
            vector<int> path;
            int sum = 0;
            for(int i = 0; i < ndVec.size(); i++){
                sum += ndVec[i]->val;
                path.push_back(ndVec[i]->val);
            }
            if(sum == targetSum)result.push_back(path);
        }
        if(curNode->left) pathSumHelper(curNode->left, result, ndVec, targetSum);
        if(curNode->right) pathSumHelper(curNode->right, result, ndVec, targetSum);
        return;
    }
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        vector<vector<int>> result;
        vector<TreeNode*> ndVec;
        pathSumHelper(root, result, ndVec, targetSum);
        return result;
    }
};

Leecode 106. 从中序与后序遍历序列构造二叉树

题目描述

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

• 示例 1:

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

• 示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

解题思路与代码展示

本题从思路上不难理解，后序遍历的最后一个数表示了当前树中的根节点，根据根节点中的值将前序序列分成两半，可以得到左右两个子树的前序序列。同时根据分割后的前序序列长度也可以将后序序列以同样的长度进行分割，得到左右子树的后序序列。从而再进行递归，即可得到整颗树的结构。故我们可以写出以下代码：

class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(inorder.empty() || postorder.empty()) return nullptr; // 处理递归终止条件，如果当前序列为空，则返回空
        int rootVal = postorder[postorder.size()-1]; // 后序序列的最后一个值即为根节点中的值
        TreeNode* root = new TreeNode(rootVal); // 新建根节点

        int cutPoint = find(inorder.begin(), inorder.end(), rootVal) - inorder.begin();  // 查找根节点在前序序列中的位置
        vector<int> leftInorder(inorder.begin(), inorder.begin()+cutPoint); // 构造左子树的前序序列
        vector<int> leftPostorder(postorder.begin(), postorder.begin()+cutPoint); // 构造左子树的后序序列

        vector<int> rightInorder(inorder.begin() + cutPoint + 1, inorder.end()); // 构造右子树的前序序列
        vector<int> rightPostorder(postorder.begin() + cutPoint, postorder.end()-1); // 构造右子树的后续序列

        root->left = buildTree(leftInorder, leftPostorder); // 对左子树进行递归 
        root->right = buildTree(rightInorder, rightPostorder); // 对右子树进行递归

        return root; 
    }
};

上面代码对两个vector进行递归即可建立整个二叉树。同时这部分有几道非常类似的题目，都是根据遍历结果构建二叉树，下面只贴出链接和相应代码，并不过多赘述。

• Leecode 105. 从前序与中序遍历序列构造二叉树

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.empty() || inorder.empty()) return nullptr;
        TreeNode* root = new TreeNode(preorder[0]);
        int cutPoint = find(inorder.begin(), inorder.end(), root->val) - inorder.begin();
        vector<int> leftPre(preorder.begin()+1, preorder.begin()+cutPoint+1);
        vector<int> leftIn(inorder.begin(), inorder.begin()+cutPoint);

        vector<int> rightPre(preorder.begin()+cutPoint+1, preorder.end());
        vector<int> rightIn(inorder.begin()+cutPoint+1, inorder.end());

        root->left = buildTree(leftPre, leftIn);
        root->right = buildTree(rightPre, rightIn);

        return root;
    }
};

• Leecode 889. 根据前序和后序遍历构造二叉树

class Solution {
public:
    TreeNode* constructFromPrePost(vector<int>& preorder, vector<int>& postorder) {
        if (preorder.empty()) return nullptr;
        
        TreeNode* root = new TreeNode(preorder[0]);
        if (preorder.size() == 1) return root;
        
        int L = 0;
        // 查找前序第二个元素（左子树根）在后序中的位置
        for (int i = 0; i < postorder.size(); ++i) {
            if (postorder[i] == preorder[1]) {
                L = i + 1; // 左子树节点数 = 位置索引 + 1
                break;
            }
        }
        
        // 分割左子树数组
        vector<int> leftPre(preorder.begin() + 1, preorder.begin() + 1 + L);
        vector<int> leftPost(postorder.begin(), postorder.begin() + L);
        
        // 分割右子树数组（修正结束位置）
        vector<int> rightPre(preorder.begin() + 1 + L, preorder.end());
        vector<int> rightPost(postorder.begin() + L, postorder.end() - 1);
        
        // 递归构建
        root->left = constructFromPrePost(leftPre, leftPost);
        root->right = constructFromPrePost(rightPre, rightPost);
        
        return root;
    }
};

今日总结

今天题目都还挺简单，最难的其实是最后刷了一道用前序+后序建立二叉树，在没有中序的情况下可能有多个解，但也需要能够想到怎么才能分割出满足条件的解，

今天力扣到60题了，再接再厉！