代码随想录第十五天 | Leecode 110. 平衡二叉树、257. 二叉树的所有路径、404. 左叶子之和、222. 完全二叉树的节点个数
Leecode 110. 平衡二叉树
题目描述
给定一个二叉树,判断它是否是 平衡二叉树(是指该树所有节点的左右子树的高度相差不超过 1。)
- 示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:true
- 示例 2:
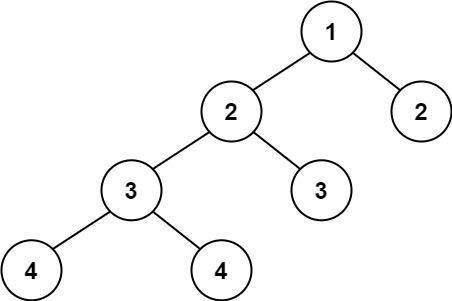
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
- 示例 3:
输入:
root = []
输出:true
递归法求高度
首先本题是需要求高度而非深度,二者的区别主要在于:
- 深度是自上往下计数
- 高度是自下往上计数
如果采用深度的方式进行递归,由于递归到某个节点的时候是自上而下进行计数,还未判断过当前节点的之下的节点,自然无法判断其是否为平衡二叉树的根节点。会导致如果漏判子树中出现非平衡二叉树、而左右子树高度都相等的情况,即下面测试用例:
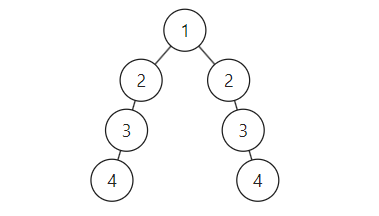
输入:
[1,2,2,3,null,null,3,4,null,null,4]
如果使用深度递归无法判断
另外,如果是采用深度递归,在递归函数的传入参数中,还有一个参数用于表示当前深度,即深度递归函数一般为:int getepth(TreeNode* curNode, int depth)。但如果是高度递归,不需要传入参数,一般形式为:int getHeight(TreeNode* curNode)。在到达空节点的时候返回0,同时在后续递归调用中进行+1操作,这样即可实现自下而上的高度递归。
下面给出本题代码:
class Solution {
public:
int getHeight(TreeNode* curNode){ // 记高度-1表示不是平衡二叉树,此时再计算高度已无意义,故记作-1
if(!curNode) return 0; // 如果当前节点为空,此时返回高度为0
int leftHeight = getHeight(curNode->left); // 获取左子节点的高度
int rightHeight = getHeight(curNode->right); // 获取右子节点的高度
if(leftHeight == -1 || rightHeight == -1) return -1; // 如果两个子节点中有一个的高度为-1,说明已经不是平衡二叉树,返回高度-1
if( abs(leftHeight - rightHeight) > 1) return -1; // 如果两个子节点高度差大于1,说明不是平衡二叉树,则返回高度-1
return max(leftHeight, rightHeight) + 1; // 当前节点的高度 = 左右两个节点中更大的高度 + 1
}
bool isBalanced(TreeNode* root) {
return getHeight(root) != -1; // 只要最后根节点的高度不为 -1, 则为真
}
};
上面代码中,需要注意的一点在于,我们将非平衡二叉树的根节点高度记作-1,原因是此时再记录其高度已经没有意义,使用高度-1并在其中增加一行判断(如果子节点的高度为-1则当前节点高度也为-1),这样可以使得一旦出现非平衡二叉树的节点,就可以一直回传到最终根节点中。
Leecode 257. 二叉树的所有路径
题目描述
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
- 示例 1:
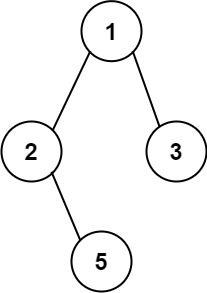
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
- 示例 2:
输入:
root = [1]
输出:["1"]
回溯递归
题外话:这题真特么难。。真的是简单题吗,给我做得怀疑人生了。。前几天刷下来感觉自己又行了,今天这一道题又给打回现实了
本题需要输出每一条通往叶节点的路径,考虑采用回溯的方法,遍历走到叶节点之后记录当前路径,然后返回进行回溯。思想上还算能够想通,但是如果没有接触过回溯的话想要实现代码还是有一定难度的(说的就是我)。下面结合代码来进行说明:
class Solution {
public:
void pathHelper(TreeNode* curNode, vector<int>& path ,vector<string>& result){ // 传入参数为:当前节点、从根节点走到当前节点的路径,用于存放结果
path.push_back(curNode->val); // 第一步先将当前节点记录到路径中
if(!curNode->left && !curNode->right){ // 如果当前节点是叶节点,将路径转换为string进行存放
string pathString = to_string(path[0]); // 从这一步开始将vector<int> 中的路径转换为string类型
for(int i = 1; i < path.size(); i++){
pathString += ("->" + to_string(path[i]));
}
result.push_back(pathString); // 将上面路径转换成的字符串存入result中
}
if(curNode->left) { // 如果当前节点不是叶节点,则需要往能走的方法继续走
pathHelper(curNode->left, path, result); // 往左子节点走下去,递归地去左子树中寻找并记录路径
path.pop_back(); // 由于使用上面递归之后,会在递归函数中传入curNode->left->val,现在递归结束回退后需要将其删除
}
if(curNode->right) { // 如果有右子节点,需要去记录右子树中的路径
pathHelper(curNode->right, path, result); // 递归右子树寻找路径
path.pop_back(); // 同样也要将右子节点给弹出
}
return;
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result; // 建立用于存放结果的vector
if(!root) return result; // 如果根节点为空,则直接返回空的vector
vector<int> path; //
pathHelper(root, path, result);
return result;
}
};
上面代码中的path.pop_back();体现了回溯的过程,但同样可以使用值传递来代替引用传递,这样可以免去这一步pop回溯。同时可以直接使用字符串来存放路径,遍历到叶节点后直接push记录即可,而不必再使用一个存放int的vector容器。故可以将代码简化如下:
class Solution {
public:
void pathHelper(TreeNode* curNode, string path, vector<string>& result){
if(curNode) path += (to_string(curNode->val) + "->");
if(!curNode->left && !curNode->right){
path.resize(path.size()-2); // 除去最后的箭头符号
result.push_back(path);
}
if(curNode->left) pathHelper(curNode->left, path, result); // path使用值传递,因此不需要回退
if(curNode->right) pathHelper(curNode->right, path, result);
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
if(!root) return result;
string path = ""; // 初始化path
pathHelper(root, path, result);
return result;
}
};
经过本题的历练,希望之后能够掌握回溯的思想。
Leecode 404. 左叶子之和
题目描述
给定二叉树的根节点 root ,返回所有左叶子之和。
- 示例 1:
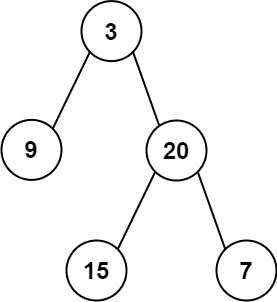
输入:root = [3,9,20,null,null,15,7]
输出:24
解释: 在这个二叉树中,有两个左叶子,分别是9和15,所以返回24
- 示例 2:
输入:
root = [1]
输出:0
递归法
题目要求只对左叶子求和,那么可以考虑使用一个布尔变量,来记录上一步遍历到当前节点的时候是往左还是往右。如果是往左来的则为true,否则为false。那么我们可以得到如下代码:
class Solution {
public:
void sumHelper(TreeNode* curNode, int &curSum, bool isLeft){ // 使用一个布尔变量来记录当前节点是否为其父节点的左子节点
if(!curNode) return; // 如果当前子节点为空,则直接返回
if(!curNode->left && !curNode->right){ // 如果当前节点是叶节点
if(!isLeft) return; // 还需要判断是否是左子节点,如果不是则直接返回
curSum += curNode->val; // 如果是题目要求得左叶节点,则将其中的值加到curSum中
return;
}
sumHelper(curNode->left, curSum, true); // 递归地对左子节点求和,需要注意此时传入的布尔变量,左为true,右为false
sumHelper(curNode->right, curSum, false); // 递归地对右子节点求和
return;
}
int sumOfLeftLeaves(TreeNode* root) {
int sum = 0;
sumHelper(root, sum, false); // 根节点不是左子节点,故一开始传入的布尔变量为false
return sum;
}
};
Leecode 222. 完全二叉树的节点个数
题目描述
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层(从第 0 层开始),则该层包含 1~ 2h 个节点。
- 示例 1:
输入:root = [1,2,3,4,5,6]
输出:6
- 示例 2:
输入:
root = []
输出:0
- 示例 3:
输入:
root = [1]
输出:1
解法1,当做普通二叉树递归求解
如果不考虑这是一颗完全二叉树,那么根据:树中节点数 = 左子树节点数 + 右子树节点数 + 1;使用该公式可以直接得到下面递归代码:
class Solution {
public:
int countNodes(TreeNode* root) {
if(root == nullptr) return 0;
return countNodes(root->left) + countNodes(root->right) + 1;
}
};
我们可以分析上面节点的时间复杂度,相当于将每个节点都遍历了一次,故时间复杂度为\(O(n)\)。接下来我们考虑利用题目中给出的当前这棵树是完全二叉树的情况,如何降低时间复杂度。
解法2 完全二叉树的节点个数
对于完全二叉树而言,如果恰好是一颗满二叉树,那么总节点个数为:深度\(d\)的平方-1,即\(2^d - 1\)。但完全二叉树并不都恰好是满二叉树,不过幸好对于每一颗完全二叉树,其子树最后都有一部分是完全二叉树。故我们可以利用这个规律,得到下面代码:
class Solution {
public:
int countNodes(TreeNode* root) {
if(!root) return 0;
TreeNode* leftNode = root->left;
TreeNode* rightNode = root->right;
int leftDep = 0;
int rightDep = 0;
while(leftNode){
leftNode = leftNode->left;
leftDep++;
}
while(rightNode){
rightNode = rightNode->right;
rightDep++;
}
if(leftDep == rightDep) return (2 << leftDep) - 1; // 左移位运算符相当于是求幂次
return countNodes(root->left) + countNodes(root->right) + 1;
}
};
上面代码利用了完全二叉树的特性,尽管看起来代码变得复杂了很多,但实际上时间复杂度比原本更低,变成了\(O(\log n* \log n)\)。在节点数增多的时候,会比原本的时间复杂度\(O(n)\)要低很多。
另外,对于上面代码中用到的左移位运算符<<,相当于是将二进制数整体左移,得到的结果相当于是乘了一个\(2^x\)的2次幂。
今日总结
今天学习了回溯的算法,需要注意回溯时如果使用引用传递则需要手动进行回溯,而如果使用值传递则不必。同时又学习了完全二叉树的特性,并充分利用其特性降低时间复杂度。
同时记录一下当前力扣刷题记录,已经到了第54题:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号