代码随想录第十三天 | Leecode 144. 二叉树的前序遍历、 94. 二叉树的中序遍历、 145. 二叉树的后序遍历

Leecode 144. 二叉树的前序遍历

• 题目链接：https://leetcode.cn/problems/binary-tree-preorder-traversal/

题目描述

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

• 示例 1：

输入：root = [1,null,2,3]
输出：[1,2,3]
解释：

• 示例 2：

输入：root = [1,2,3,4,5,null,8,null,null,6,7,9]
输出：[1,2,4,5,6,7,3,8,9]
解释：

• 示例 3：

输入：root = []
输出：[]

• 示例 4：

输入：root = [1]
输出：[1]

前序遍历介绍

对于前序遍历而言，描述一个树的时候，需要先说明树的根节点，然后是左子节点，最后再右子节点，同时如果子节点又作为一个子树的根节点，那么需要以同样的方式遍历其子树。即：

• 输出当前根节点
• 输出根节点的左子节点（如果该节点作为树的根节点，则需要重新调用当前规则输出这个子树）
• 输出根节点的右子节点（如果该节点作为树的根节点，同样需要重新调用当前规则输出这个子树）

上面这个递归思想即可得到递归遍历算法的雏形，同时为了说明演示先序遍历的效果，下面可以给出一个例子，可以非常方便的自己在草稿纸上推出一个二叉树的先序遍历。

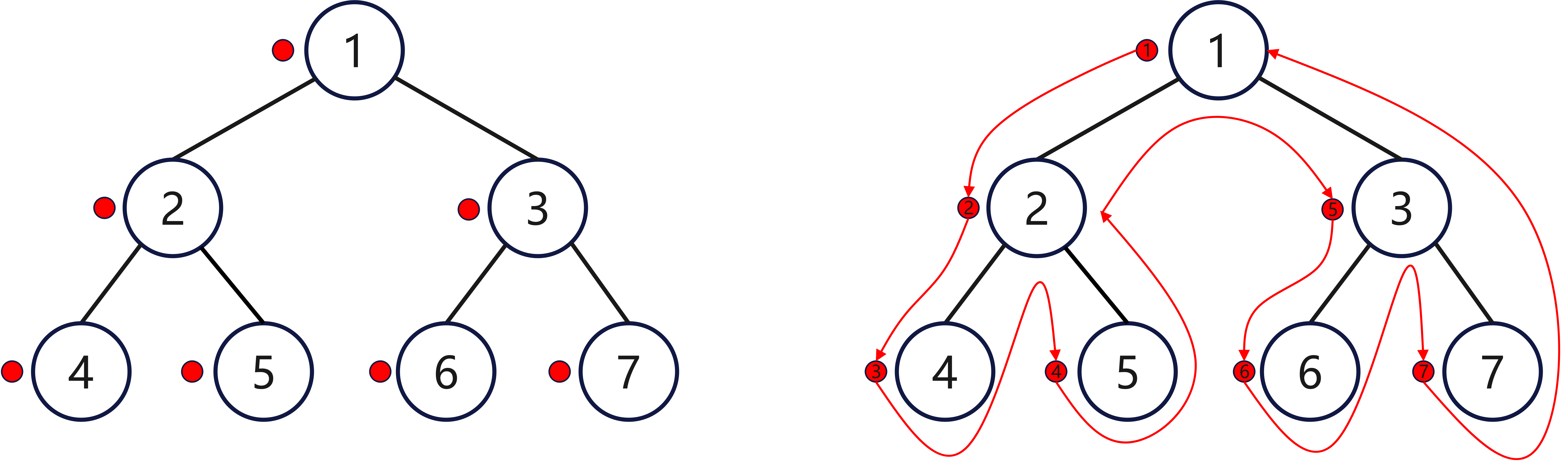
• 对于一个如下所示的高度为3，有7个节点的满二叉树，如果要求其先序遍历，在草稿纸上画出其图像后，在其中每个节点的左侧做一个标记，随后从根节点左侧开始，围绕二叉树的外侧画出一条曲线，记录依次经历过每个节点左侧标记的顺序，此时所得的顺序即为先序遍历，示意图如下：
  
  由上面图像可以看出，此时的先序遍历序列为：[1, 2, 4, 5, 3, 6, 7]。

解法1 递归法进行先序遍历

根据上一节所说的先序遍历定义，可以直接写出递归下遍历的代码：

class Solution {
public:
    void preorderTraversalHelper(TreeNode* root, vector<int>& vec){ // 使用一个void类型的Helper函数辅助递归
        if(root == nullptr) return; // 如果当前节点为空，则返回
        vec.push_back(root->val); // 先序遍历则需要将当前节点先放入vector中
        preorderTraversalHelper(root->left, vec); // 向左遍历
        preorderTraversalHelper(root->right, vec); // 向右遍历
    }

    vector<int> preorderTraversal(TreeNode* root) { 
        vector<int> result; // 新建一个用于存放结果的vector数组
        preorderTraversalHelper(root,result); // 进行递归遍历
        return result; // 输出结果
    }
};

上面代码中，通过定义一个辅助遍历函数，从而完成了二叉树的先序遍历。需要注意的是，在先序遍历的辅助函数中，是先进行push_back()操作，随后再递归调用左子节点和右子节点。

解法2 迭代进行先序遍历

函数递归的底层是使用栈来实现的，我们同样也可以使用栈来实现递归能够实现的算法。本节使用栈来存放节点，同样可以实现先序遍历。但是需要注意的是，对于一个节点，如果要其输出顺序按照根节点->左子节点->右子节点这样的顺序输出的话，那么我们在入栈的时候需要相反的方式进行入栈。将根节点入栈后出栈记录，随后先将其右子节点入栈，再将左子节点入栈，这样才能实现先输出左子节点的先序遍历，具体代码实现如下：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result; // 定义result数组，用于存放结果
        if(root == nullptr) return result; // 如果根节点为空，则直接返回当前空的结果
        stack<TreeNode*> nodeStk;  // 新建一个用于存放节点指针的栈
        nodeStk.push(root); // 初始化栈，先在其中存放一个根节点，方便后续使用while循环中判断栈为空则说明已经遍历结束
        while(!nodeStk.empty()){ // 如果栈中没有节点，则说明已经遍历结束
            TreeNode* curNode = nodeStk.top(); // 用curNode记录当前栈顶的节点
            nodeStk.pop();  // 将栈顶节点pop出栈
            result.push_back(curNode->val); // 将出栈节点的数值存放在result中，后续再处理其左右两个子节点
            if(curNode->right != nullptr) nodeStk.push(curNode->right); // 如果节点的右子节点不为空，则需要入栈；注意此时是右子节点先入栈
            if(curNode->left != nullptr) nodeStk.push(curNode->left); // 如果节点的左子节点不为空，需要入栈
        }
        return result;
    }
};

使用上面的循环迭代也能同样实现和递归效果一致的先序遍历算法。

Leecode 94. 二叉树的中序遍历

• 题目链接：https://leetcode.cn/problems/binary-tree-inorder-traversal/description/

题目描述

给定一个二叉树的根节点 root，返回 它的 中序 遍历 。

• 示例 1：

输入：root = [1,null,2,3]
输出：[1,3,2]

• 示例 2：

输入：root = []
输出：[]

• 示例 3：

输入：root = [1]
输出：[1]

中序遍历介绍

对于中序遍历，先介绍其遍历顺序的定义。中序顾名思义，就是将当前节点遍历的顺序放到左右两个子节点之间，故称之为“中”。由此我们可以得到下面遍历顺序：

• 先遍历左子节点（左子树）
• 遍历当前根节点
• 遍历右子节点（右子树）

其中每次遍历左右子节点的时候，如果子节点下也是子树，则遍历该子树的时候同样也要按照这个顺序输出。同样我们这里也可以给出一种类似于上面先序遍历的简便记忆方法，能够帮助我们快速在草稿纸上推导出一个二叉树的中序遍历结果

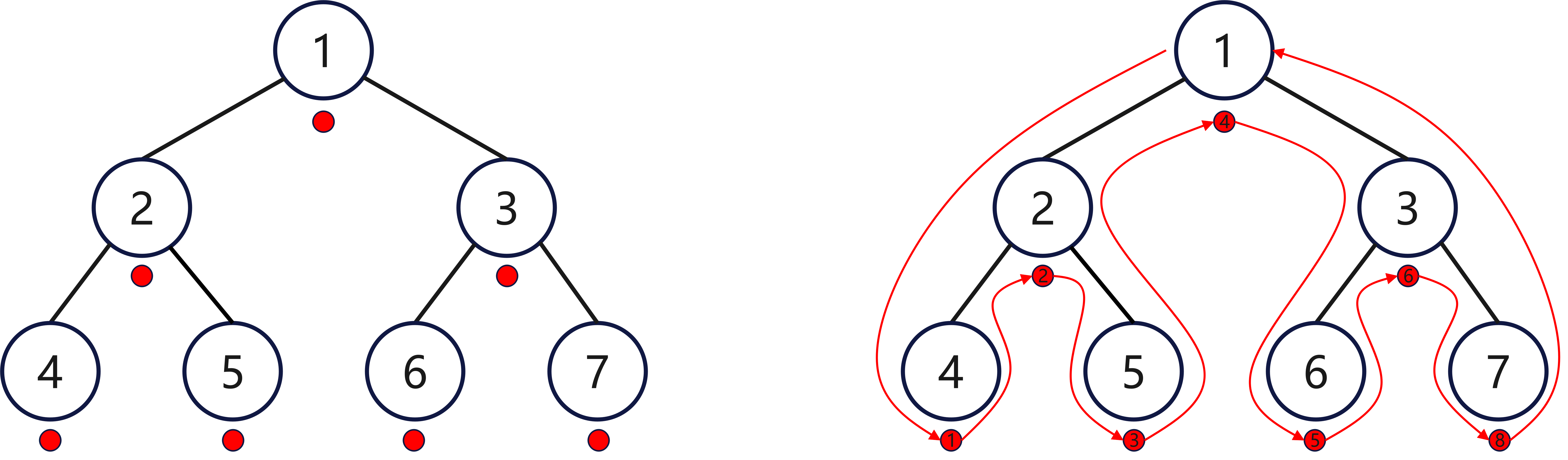
同样还是先序遍历中所展示的那一颗如下所示的高度为3，有7个节点的满二叉树，如果要求其中序遍历，在草稿纸上画出其图像后，在其中每个节点的下方做一个标记，随后从根节点左侧开始，围绕二叉树的外侧画出一条曲线，记录依次经历过每个节点下方标记的顺序，此时所得的顺序即为中序遍历，示意图如下：

由上面图像可以看出，此时的中序遍历序列为：[4, 2, 5, 1, 6, 3, 7]。

解法1 使用递归进行中序遍历

如果使用递归来进行二叉树的中序遍历，此时的代码与先序遍历的代码非常相似，区别仅在于辅助函数中的遍历顺序中，将当前节点的数插入的指令放在哪里。我们可以得到代码如下所示：

class Solution {
public: 
    void inorderTraversalHelper(TreeNode* root, vector<int>& vec){
        if(root == nullptr) return;
        inorderTraversalHelper(root->left,vec);
        vec.push_back(root->val);    // 与先序遍历的区别仅在于将当前值push_back这一行放在了递归调用左右节点之间，放在中间故称为中序遍历
        inorderTraversalHelper(root->right,vec);
    }
    vector<int> inorderTraversal(TreeNode* root) { // 主函数部分与先序遍历完全一致
        vector<int> result;
        inorderTraversalHelper(root, result);
        return result;
    }
};

上面就是使用递归实现的中序遍历的代码，其中和先序遍历的区别仅在于辅助函数Helper中，将push_back()操作放到了递归调用两个左右子节点之间。

解法2 迭代法实现中序遍历

同样地，我们也可以使用迭代法来实现上面递归实现的中序遍历算法，也是需要用到栈这个数据结构：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) { 
        vector<int> result; // 新建一个vector用于存放遍历输出结果
        stack<TreeNode*> nodeStk; // 新建一个栈用于存放节点
        TreeNode* cur = root; // cur指向初始根节点
        while(cur || !nodeStk.empty()){ // 如果当前节点为空，同时栈也为空，说明遍历已经结束
            while(cur){ // 先将cur指向当前的最左子节点，只要还不为空就一直往左下走
                nodeStk.push(cur); // 将经过的每个节点都入栈，便于之后回退
                cur = cur->left;
            } 
            cur = nodeStk.top(); // 将当前栈顶节点出栈，此时栈顶元素一定为当前所在子树的最左下角，最优先出栈
            nodeStk.pop(); 
            result.push_back(cur->val); // 将出栈的节点记录到result中
            cur = cur->right; // 转向右子树（如果右子树为空，后续会直接回退至栈顶节点）
        }
        return result;
    }
};

上面代码即可使用迭代的方式中序遍历整个二叉树，此时可以看出，使用迭代的方法下，中序遍历与前序遍历的代码完全不同。并不会展现出像递归法中只需要调换两行代码的位置即可完成转换这种情况。

Leecode 145. 二叉树的后序遍历

• 题目链接：https://leetcode.cn/problems/binary-tree-postorder-traversal/

题目描述

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历。

• 示例 1：

输入：root = [1,null,2,3]
输出：[3,2,1]
解释：

• 示例 2：

输入：root = [1,2,3,4,5,null,8,null,null,6,7,9]
输出：[4,6,7,5,2,9,8,3,1]
解释：

• 示例 3：

输入：root = []
输出：[]

• 示例 4：

输入：root = [1]
输出：[1]

后续遍历介绍

对于后序遍历，先介绍其遍历顺序的定义。类似又区别于前面提到的两种遍历顺序，后序遍历需要先遍历输出左右两个子树，最后再输出当前根节点。即我们可以得到遍历顺序如下：

• 先遍历左子节点（左子树）
• 遍历右子节点（右子树）
• 遍历当前根节点

与之前类似，上面遍历左右子节点的过程中，如果子节点下为一颗子树，则需要按照同样的方式递归遍历其子树中的每一个节点。对于后续遍历我们也可以给出一种方便手动推导顺序的方式，通过下面例子给出:

使用之前两种遍历中所展示的那一颗如下所示的高度为3，有7个节点的满二叉树，如果要求其后序遍历，在草稿纸上画出其图像后，在其中每个节点的右侧做一个标记，随后从根节点左侧开始，围绕二叉树的外侧画出一条曲线，记录依次经历过每个节点右侧标记的顺序，此时所得的顺序即为后序遍历，示意图如下：

由上面图像可以看出，此时的后序遍历序列为：[4, 5, 2, 6, 7, 3, 1]。

使用类似于上面的方式，我们可以手动快速地在一个图像中得到相应的二叉树的先、中、后序遍历，区别仅在于这几种方式使用时，标记所处的不同的地方（先序在左、中序在下，后序在右）。

解法1 递归法求二叉树后序遍历

介绍了前面用递归法进行先序和中序的代码后，我们此时再介绍采用递归进行后续遍历的算法也非常简单了，同样也是只需要修改递归辅助函数中插入当前值的位置即可，具体代码如下：

class Solution {
public:
    void postorderTraversalHelper(TreeNode* root, vector<int>& vec){
        if(root == nullptr) return;
        postorderTraversalHelper(root->left,vec);
        postorderTraversalHelper(root->right,vec);
        vec.push_back(root->val);  // 将当前节点的值push到vector中，后序遍历的push位于遍历左、右子节点之后。
    }
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        postorderTraversalHelper(root,result);
        return result;
    }
};

使用上面代码即可使用递归完成二叉树的后序遍历。

解法2 迭代法进行后序遍历

后序遍历可以采用和先序遍历类似的方法实现，因为先序遍历的顺序为“中，左，右”；而后序的顺序为“左，右，中”。那么可以通过将先序遍历中先将右节点入栈转换为先将左节点入栈，那么输出顺序就变成了“中，右，左”，然后此时只需要将最后的数组进行一次reverse反转即可得到最终的结果。那么可以根据这个思路得到代码如下：

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> nodeStk;
        if(root == nullptr) return result;
        nodeStk.push(root);
        while(!nodeStk.empty()){
            TreeNode* cur = nodeStk.top();
            nodeStk.pop();
            result.push_back(cur->val);
            if(cur->left) nodeStk.push(cur->left); // 先将左节点压栈
            if(cur->right) nodeStk.push(cur->right); // 再将右节点压栈
        }
        reverse(result.begin(),result.end()); // 最后将结果进行一次反转
        return  result;
    }
};

上面代码相当于复用了先序遍历迭代法的代码，通过在上面修改得到了后序遍历的输出。此后设计算法的时候也需要学会借鉴已有代码的思想。

今日总结

今天复习了先序、中序、后序遍历，使用递归法遍历非常简单，主要难点在于使用迭代法进行遍历的时候，需要手动使用栈来模拟整个遍历过程，还是具有一定难度的。特别是中序遍历，真的想了很久才把它给写出来。

另外按层遍历今天时间不够了暂时没写，准备明天把题刷一下就行了，总共10道题全部写在博客也太要命了。