代码随想录第四天 | Leecode 24. 两两交换链表、19.删除链表的倒数第N个节点、 面试题 02.07. 链表相交、 142.环形链表II

Leecode 24 两两交换链表

题目描述

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

• 示例 1：
  

  • 输入：head = [1,2,3,4]
  • 输出：[2,1,4,3]

• 示例 2：

  • 输入：head = []
  • 输出：[]

• 示例 3：

  • 输入：head = [1]
  • 输出：[1]

递归法解题思路

本题要求每一次对链表的最前端两个节点进行交换，而每次交换结束之后，后续的链表又可以看做是一个新的链表。故自然可以联想到使用递归的方法，此处给出递归算法的算法框架：

• 调用递归函数对后续链表进行两两交换
  • 处理终止条件（如果当前链表为空，则返回nullptr，如果当前链表只有一个节点，则返回当前头节点）
  • 对链表中头两个节点进行交换操作
  • 交换后的后一个节点指向对后续链表头节点调用递归函数的返回值

根据上面思路可以写出代码如下：

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(head == nullptr){ // 链表为空的时候
            return nullptr;
        }
        else if(head->next == nullptr){ // 链表中只有一个节点
            return head;
        }
        ListNode* pre = head;  // pre和cur分别指向最前的两个节点
        ListNode* cur = head->next;
        pre->next = swapPairs(cur->next);  // 对后续节点递归调用
        cur->next = pre;  
        return cur;
    }
};

上面这个递归算法感觉也算比较容易理解了，和昨天那道移除链表元素的方法很像，那道题每次递归只用判断头节点是否需要删除，而本题每次只用对前两个节点进行交换。同时这题我也是二十分钟不到一遍提交直接通过，这还是我到目前为止第一道一遍过的题目。

Leecode 19 删除链表的倒数第n个节点

• 题目链接：https://leetcode.cn/problems/remove-nth-node-from-end-of-list/description/

题目描述

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

• 示例 1：
  
  • 输入：head = [1,2,3,4,5], n = 2
  • 输出：[1,2,3,5]
• 示例 2：
  • 输入：head = [1], n = 1
  • 输出：[]
• 示例 3：
  • 输入：head = [1,2], n = 1
  • 输出：[1]

解法1 两次遍历的暴力求解

本题需要删除倒数第n个节点，但是链表并不能从末尾往前遍历。因此一种自然的想法就是，先遍历一遍链表来计数数出链表中节点的个数k，那么要删除倒数第n个节点，就相当于删除第k-n个节点。后续直接再遍历一次查找到待删除的节点的前一个节点（即第k-n-1个节点）即可删除节点。

按照上述思路可以得到代码如下：

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        int k = 1;
        ListNode* cur = head; 
        while(cur->next){  // 用k来记录链表中元素个数
            cur = cur->next;
            k++;    
        }
        if(k < n) return head; // 如果链表中元素更少，则直接返回
        else if(k == n) return head->next;  // 如果链表中元素个数和n相等，返回下一个节点
        else{
            cur = head; // cur指针重新回到head头节点
            for(int i = 0; i < k-n-1; i++){ // 往后走 k-n-1 步，走到待删除的节点的前一个节点
                cur = cur->next;
            }
            ListNode* temp = cur->next; // 删除节点
            cur->next = cur->next->next;
            delete temp;
        }
        return head;
    }
};

可以分析一下上面代码的时间复杂度，首先进行一次遍历进行计数，时间复杂度为\(O(n)\)，随后再进行删除操作，时间复杂度又是\(O(n)\)。因此相当于进行了两次复杂度为\(O(n)\)的操作，因此总的时间复杂度还是\(O(n)\)。

解法2 双指针法

刚才的方法用了两次遍历，接下来我们考虑只使用一次遍历。为了取到倒数第n个节点的前一个节点，我们可以让一个指针先出发进行遍历，在走了n+1步之后，第二个指针从头节点出发；当第一个指针走到末尾之后，第二个指针就指向了倒数第n个节点的前一个节点。使用这样的方法，我们可以得到代码如下：

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* right = head;
        for(int i = 1; i < n; i++){ // 第一个指针先出发走步n步
            if(right == nullptr){ // 如果数组长度小于n，则会先走到null，那么不用删除直接返回
                return head;
            }
            right = right->next;
        }
        if(right->next == nullptr) return head->next; // 如果链表中刚好n个节点，那么删去头节点
        right = right->next;    // 右指针多走一步，因为左指针要指向待删除节点的上一个节点
        ListNode* left = head; // 左节点进入链表
        while(right->next){
            right = right->next;
            left = left->next;
        }
        ListNode* temp = left->next;
        left->next = left->next->next;
        delete temp;
        return head;
    }
};

上面代码中只用一次遍历就完成，而时间复杂度和之前一样还是\(O(n)\). 但的确是会更加高效一些.

Leecode 面试02.07 链表相交

• 题目链接： https://leetcode.cn/problems/intersection-of-two-linked-lists-lcci/description/

题目描述

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交：

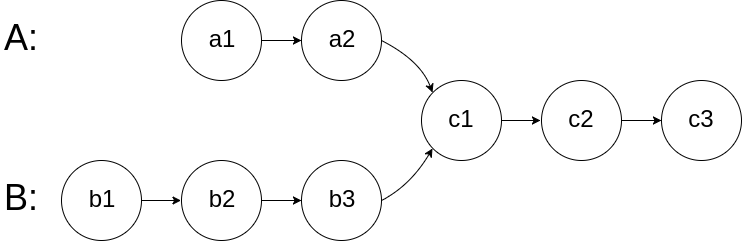
题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

• 示例 1：
  

  • 输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
  • 输出：Intersected at '8'
  • 解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。从各自的表头开始算起，链表 A为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

• 示例 2：
  

  • 输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
  • 输出：Intersected at '2'
  • 解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

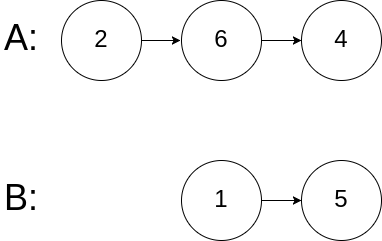
• 示例 3：
  

  • 输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
  • 输出：null
  • 解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。这两个链表不相交，因此返回 null 。

解法1 暴力法

还是先来一个暴力搜索，考虑每次固定链表A中的一个节点，逐个比较链表B中的所有节点，如果从头到尾比对完都没有，那么选取A的下一个节点继续比对链表B中的节点。这种算法的时间复杂度为\(O(m \times n)\)，其中\(n\)和\(m\)分别表示链表A和链表B中节点个数，但尽管时间复杂度很大，我们也可以先把这种算法写出来：

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        for(ListNode* curA = headA;curA != nullptr; curA = curA->next){ // 遍历A中每一个节点
            for(ListNode* curB = headB; curB != nullptr; curB = curB->next){ // 每次固定A的一个节点，遍历B中所有节点
                if(curA == curB){ // 如果存在一样的节点，则说明相交，返回当前节点
                    return curA;
                }
            }
        }
        return nullptr; // 如果遍历完所有节点都没有找到，那就返回空指针
    }
};

非常暴力又有效的算法，上面代码也很简洁，短短几行就遍历完了所有情况。但是又不得不说时间复杂度为\(O(m \times n)\)还是有点太大，接下来我们考虑另外一种时间复杂度为\(O(m + n)\)的算法。

解法二

根据相交链表示意图可以看出，两个相交链表在相交之后共用相同的一组后缀节点，而这两个链表在相交之前的长度我们是未知的。为了能够找到两个链表相交的节点，我们可以考虑让长度更长的一个链表先往后遍历几步，等到该链表剩下的部分和另外一个链表长度一样的时候，再让这两个链表一起遍历，同时每一步遍历都进行一次判断，如果两节点相等，则说明找到了相交节点。下面我们可以给出代码：

class Solution {
public:
    int countNode(ListNode* head){ // 输出链表中节点的个数
        if(head == nullptr) return 0; // 如果头节点为nullptr，则说明长度为0
        ListNode* cur = head;
        int n = 1;  // 头节点是第一个节点
        while(cur){  // 遍历计数
            cur = cur->next; 
            n++;
        }
        return n;
    }

    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        int n_A = countNode(headA);  // 首先取到两个链表的长度
        int n_B = countNode(headB);
        if ( n_A == 0 || n_B == 0){  // 如果有一个链表为空，则直接返回nullptr
            return nullptr;
        }

        ListNode* curA = headA;  // 初始化遍历指针
        ListNode* curB = headB;
        if(n_A > n_B){  // 如果链表A更长，则指针curA先走几步；// 这里的if-else判断可以删掉，只留下两个for循环也可，因为for循环中i < n_A - n_B已经包含了判断
            for(int i = 0; i < n_A-n_B ; i++){
                curA = curA->next;
            }
        }
        else{ // 如果链表B更长，则指针curB先走几步；// 这里的if-else结构可以删除，为了可读性而进行保留
            for(int i = 0; i < n_B-n_A ; i++){
                curB = curB->next;
            }
        }  // 刚才单独操作一个指针，使得现在两个指针到最后的距离相等，接下来两个指针一起遍历，并每一次遍历都进行if判断
        while(curA){ 
            if(curA == curB){  // 如果两个指针相同，则说明找到了交叉点，此时return该节点
                return curA; 
            }
            curA = curA->next;  // 两个指针一起往后走
            curB = curB->next;
        }
        return nullptr; // 如果两个链表都遍历完了还没找到相交点，则说明无相交，返回nullptr
    }
};

上面这个算法的时间复杂度为\(O(m+n)\)。相比刚才的\(O(m\times n)\)已经得到了较大优化.

Leecode 142 环形链表

• 题目链接：

题目描述

给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

• 示例 1：
  

  • 输入：head = [3,2,0,-4], pos = 1
  • 输出：返回索引为 1 的链表节点
  • 解释：链表中有一个环，其尾部连接到第二个节点。

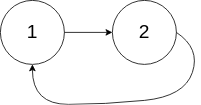
• 示例 2：
  

  • 输入：head = [1,2], pos = 0
  • 输出：返回索引为 0 的链表节点
  • 解释：链表中有一个环，其尾部连接到第一个节点。

• 示例 3：
  

  • 输入：head = [1], pos = -1
  • 输出：返回 null
  • 解释：链表中没有环。

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head; // 定义快慢指针
        ListNode* slow = head;
        while(1){
            if(fast == nullptr || fast->next == nullptr) return nullptr; // 如果快指针走到null说明没有环

            fast = fast->next->next;  // 快慢指针分别移动
            slow = slow->next;
            if(fast == slow) break; // 如果快慢指针相交，说明存在有环
        }
        slow = head;  // 两个指针分别再从相交点和头节点开始遍历，再次的交点就是入环的节点
        while(1){
            if(fast == slow) return fast;  // 如果两个节点再次汇合，此时节点就是入环的节点
            fast = fast->next;
            slow = slow->next;
        }
    }
};

这道题感觉难度还真挺大的，感觉就是需要比较巧妙的数学推导才能想到这个方法。我是想了很久没有想出来，最后看了一下卡哥的文档才知道怎么做。

今日总结

今天写了了链表的四道题目，也算是粗略地把链表过完了。感觉链表和数组部分的题目用了很多双指针的方法，以及很多题目都可以用递归（这几天写了好多递归）

最后给自己加油