代码随想录第二天 | Leecode 209. 长度最小的子数组、59. 螺旋矩阵II
Leecode 209 长度最小的子数组
题目描述
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
-
示例 1:
- 输入:
target = 7,nums = [2,3,1,2,4,3] - 输出:
2 - 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
- 输入:
-
示例 2:
- 输入:
target = 4,nums = [1,4,4] - 输出:
1
- 输入:
-
示例 3:
- 输入:
target = 11,nums = [1,1,1,1,1,1,1,1] - 输出:
0
- 输入:
-
提示:
1 <= target <= 10^91 <= nums.length <= 10^51 <= nums[i] <= 10^4
解法1 暴力解法
这道题让找到连续求和大于等于目标值的子数组,很容易能想到一个暴力解法,那就是遍历可能的区间长度,先找长度为1的子数组有没有合适的,再依次找长度为\(2, 3, \dots, n\)的子数组有没有满足题目条件的长度,如果有则立即跳出循环输出这个长度;如果遍历完所有可能的子数组都没有的话,就输出0.
这个暴力解法中,所有可能取到的子数组有\(1+2+\cdots+n \sim n^2\)种,即遍历完所有子数组的复杂度为\(O(n^2)\),每个子数组求和的时间复杂度又是\(O(n)\),因此总共需要的时间复杂度大致上是\(O(n^3)\)的数量级。这是一个非常非常大的时间复杂度,但我们也能给出这种解法的代码如下:
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
bool found = false; // 用一个布尔变量来存储是否找到这样的子数组
int i = 1; //先搜索长度为1的子数组
for(; i <= nums.size(); i++){ // 遍历子数组长度可能取到的值
for(int j = 0; j + i - 1 < nums.size() ; j++){ // 遍历子数组区间,左侧从0开始,长度为i的数组的最右侧序号j+i-1
int sum = 0; //每个区间的总和进行初始化
for(int k = 0; k < i; k++){ //计算区间的总和
sum += nums[k+j];
}
if(sum >= target) { // 如果找到目标值,则将布尔变量转换为true
found = true;
}
if(found) break; // 找到之后则一直break直至退出
}
if (found) break;
}
if(found) return i;
else return 0;
}
};
上面代码也可以看出,用了三层for循环,时间复杂度大致上为\(O(n^3)\)。真的是一个非常可怕的时间复杂度,题目告诉1 <= nums.length <= 10^5,那么如果原数组长度为\(10^5\),那么需要计算的计算量在\(10^{15}\)这个数量级。将这段代码输入并进行提交,可以看到通过了18个测试样例,而剩余的测试样例因为超时而无法通过。由此也可以知道这段代码起码是正确的,但是时间复杂度实在过高。为此我们需要考虑其他时间复杂度更低的算法。
解法2 双指针滑动窗口
上面算法中用了3层for循环,这里我们考虑仅使用一次for循环就能求出符合条件的最小数组。
考虑用两个指针left和right来表示一个连续的子数组,用这两个指针及其之间的元素来表示这是连续子数组。
而两个指针移动的过程就可以看做是这个子数组的长度发生变化,我们规定一开始指针left和right都在0号位置,只能往右移动,且有left <= right恒成立,那么有:
right指针右移,相当于使得子数组变长,子数组总和增大left指针右移,相当于使得子数组变短,子数组总和减小
那么对于这个子数组中所有元素的和有两种情况:
- 子数组的总和大于或等于
target目标值,那么此时需要试探该数组能否变小 - 子数组的总和小于
target目标值,那么此时需要往子数组中增加更多元素,使得和更大而尽可能满足条件
那么现在我们考虑将两个指针从左到右依次扫过数组,根据每个状态下子数组的和来动态决定下一次该移动哪个指针,如果满足条件就尝试能否减小,如果不满足条件就尝试新增一个元素。并记录这个过程中能否存在满足的情况的布尔变量,若能满足还需要记录满足条件的所有情况中的最小长度。由此即可设计算法得到如下代码:
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int left = 0; // 初始化左右指针,用左右指针指向和二者中间的元素来表示子数组
int right = 0;
int curSum = nums[0]; // 初始条件下的子数组仅包含第一个元素,故子数组的初始总和即为第一个元素的值
int minLen = nums.size(); // 记录如果可以满足条件,最小的子数组长度
bool found = false; // 记录是否能找到满足条件的子数组的布尔变量
for(int i = 0; i < 2*nums.size(); i++){ // 两个指针依次扫过整个数组,每次只移动一个指针,因此最多只需要循环 2*nums.size() 次即可
if(curSum < target && right < nums.size() - 1){ // 当前没有满足条件,此时应将数组变大,但同时需要确保 right 指针没有走到最后
right += 1; // right 指针向右移动一位,相当于子数组长度扩大一位
curSum += nums[right]; // 子数组总和加上新加入的元素
}
else if(curSum < target && right == nums.size()-1){ // 当前没有满足条件,此时应将数组变大,但若right指针已经走到最后,无法扩大,故直接退出
break;
}
else{ // 当前已经满足条件,应试探能否将数组减小
if (right - left + 1 < minLen) minLen = right - left + 1; // 如果满足条件情况下,数组长度更短,则更新最短长度的记录
found = true; // 更新布尔变量表示已经找到
curSum -= nums[left]; // 在子数组和中减去马上要被移走的值
left += 1; // left 右移一位,
if(left > right){ // 如果出现left > right的这种异常,说明刚才满足条件的子数组中只有一个元素,并且刚记录的最小长度minLen = 1
break; // 只有一个元素就满足的情况是理想中最好的情况,此时直接退出即可
}
}
}
if(found) return minLen; // 如果存在满足条件的情况,则返回记录的最小长度
else return 0; // 如果不存在,那么返回0
}
};
就这样我们完成了仅用一个for循环就找到最小数组的情况,分析可以知道时间复杂度变成了\(O(n)\). 提交之后也是顺利通过了所有测试算例.
个人觉得本解法最重要的点在于,需要明确抽象用哪几个量来表示状态(表示状态的是一个五元组(left, right, curSum, minLen, found)),以及在当前状态下应该执行什么命令。在明确这一点之后再去编写代码那就非常清晰了。
Leecode 59 螺旋矩阵 II
题目描述
给你一个正整数 n ,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
-
示例 1:
![]()
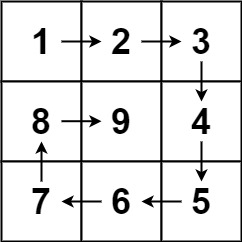
- 输入:n = 3
- 输出:[[1,2,3],[8,9,4],[7,6,5]]
-
示例 2:
- 输入:n = 1
- 输出:[[1]]
采用递归进行模拟--解题思路
本题需要用数字螺旋增长并逐渐填满一个正方形矩阵,从最简单的情形出发逐渐思考当矩阵变大的情况
- 当
n = 1时,只需填上唯一的一个位置即可, - 当
n = 2时,需要依次填上四个方格,按照左上 -> 右上 -> 右下 -> 左下的顺序进行填充 - 当
n = 3时,需要先依次填充外侧上 -> 右 -> 下 -> 左的一圈,最后剩下一个中心的方格,与n = 1的情况类似 - 当
n = 4时,同样也是先依次填充外侧上 -> 右 -> 下 -> 左的一圈,但最后剩下一个\(2 \times 2\)的方格,与n = 2的情况类似 - \(\cdots\)
- 当
n = 奇数时,先填充外侧一圈,剩下中心再填充一个\((n-2) \times (n-2)\)的方格,并最终会递归到n = 1的情形 - 当
n = 偶数时,先填充外侧一圈,剩下中心再填充一个\((n-2) \times (n-2)\)的方格,并最终会递归到n = 2的情形
由这里分析的思路,我们只需要用代码实现n = 1,n = 2的情形,以及实现填充最外侧一圈的这个操作就行了。甚至我们再进一步分析可以发现,对于n = 2的这种情形可以看做是只进行了一次填充最外侧一圈的操作,只是其中每条边是由一个左闭右开区间框出来的一个元素。由此我们可以写出我们的递归算法框架如下:
- 递归填充函数(当前需要填充的正方形边长,当前开始的第一个数,已经填充完外侧的矩阵)
- 终止条件:已经填充完成(待填充边长 <= 0)
- 处理特殊情形:对待填充边长为1的情况进行特殊处理
- 填充最外侧一圈
- 继续调用递归函数(边长-2,下一步开始的第一个数,继续传入未填充完内部的矩阵)
采用递归进行模拟算法--C++代码展示
根据上面的算法,可以进行如下的代码实现:
#include <vector>
using namespace std;
class Solution {
public:
vector<vector<int>> generateMatrix(int n, int start = 1, vector<vector<int>> matrix = {}) {
if (matrix.empty()) { // 如果矩阵还没初始化,则新建一个 n x n 的全0矩阵
matrix = vector<vector<int>>(n, vector<int>(n, 0));
}
int total_size = matrix.size(); // 最开始的矩阵的真实边长
int row_start = (total_size - n) / 2; // 当前要填充的子矩阵的最左上角所在行(第一个元素所在行)
int col_start = row_start; // row_start 和 col_start 组成了本次递归需要填充的子矩阵的第一个元素的坐标
if(n <= 0) return matrix; // 处理终止条件,若待填充矩阵边长 n <= 0 表示已经填充完毕,直接返回即可
if(n == 1){ // 处理最后只需要填充一个方格的 1 x 1矩阵的情况
matrix[row_start][col_start] = start++;
return matrix;
}
if(n >= 2){
for(int i = 0; i < n-1; i++){ // 最上一行从左往右填充
matrix[row_start][col_start++] = start++;
}
for(int i = 0; i < n-1; i++){ // 最右一行从上往下填充
matrix[row_start++][col_start] = start++;
}
for(int i = 0; i < n-1; i++){ // 最下一行从右往左填充
matrix[row_start][col_start--] = start++;
}
for(int i = 0; i < n-1; i++){ // 最左一行从下往上填充
matrix[row_start--][col_start] = start++;
}
}
return generateMatrix(n-2, start, matrix); // 下一次填充的矩阵边长为n-2,往其中填充的第一个数为start,以及接下来需要继续填充的矩阵matrix
}
};
本题的递归写法又再一次使用了默认参数的方法。因为如果是采用递归的方法,递归函数需要能够传递一些必要的信息。在本题中需要传递的信息就包括:接下来要填充的第一个数start、已经填充了一半的矩阵martix。而原题目中一开始的输入只有一个n,故必须使用默认参数来提供一开始的初始值,而随后再使用递归调用的时候其中的值就可以自己设定了。
今日总结
不得不说今天这两道题都确实有点难度,都卡了不少的时间,而且两道题都是看了一下卡哥的思路才想出来的。不过也就仅限于思路部分,第一道看了一下文档里双指针移动的演示动画之后就自己想到了这个思路,而第二道就参考了一下左闭右开区间的设置;随后两道题目的代码部分都是全部自己独立完成的。
再总结一下今天刷题的收获:
- 学习了移动窗口的算法
- 个人感觉本质上是去思考使用尽可能少的循环,来减少时间复杂度。包括昨天的双指针也是,如果能用两个指针在一次遍历之下就把活给干了那就省了之后遍历很多次了
- 使用了非常巧妙的递归算法来模拟填充螺旋矩阵(递归思想真的太巧妙了,写完感觉很爽)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号