题解：P9697 [GDCPC 2023] Canvas

节选自：图论做题记录（三）（2025.5.24 - 2025.31）

首先，后面的操作可能会覆盖掉前面的操作，这很不好做，于是我们考虑倒着来考虑，一旦一个操作执行了，那么对应的 \(l_i\) 和 \(r_i\) 位置的数就一定是 \(x_i\) 和 \(y_i\) 了，后续所有操作均是在倒序下的，最终把答案倒着数出来就可以了。

一个显然的贪心就是，最开始执行所有 \((l_i, 2, r_i, 2)\) 操作，最后执行所有 \((l_i, 1, r_i, 1)\) 操作。那么现在我们需要处理的就是 \((l_i, 1, r_i, 2)\) 操作和 \((l_i, 2, r_i, 1)\) 操作的顺序。其实这两种操作是一样的，对于 \((l_i, 2, r_i, 1)\) 操作，我们交换 \(l_i\) 和 \(r_i\)，此时就只有 \((l_i, 1, r_i, 2)\) 操作了。我们考虑到，如果若干个修改长成如图所示的样子：

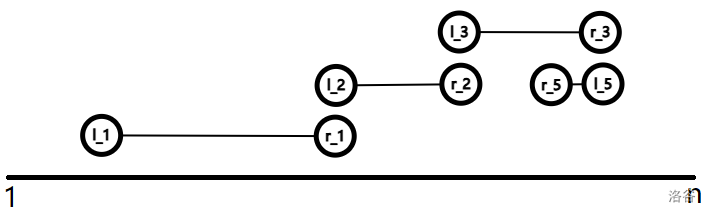
也就是每个操作的 \(l_i\) 节点正好是某个操作的 \(r_i\) 节点，那么除了 \(l_1\) 这个点，其它所有点都可以被赋值成 \(2\)，因此，我们从 \(l_i\) 向 \(r_i\) 连一条有向边，然后将这个图缩点，那么每个强连通分量中，除了入度为 \(0\) 的这个点，其它所有点都会被赋值成 \(2\)。我们在建图时，直接把边权赋值成操作编号，然后 DFS 一遍就可以确定顺序了。

最后还有一点，如果某个强连通分量中有一个点 \(u\) 被包含在了某个 \((u, 2, v, 2)\) 中，如图：

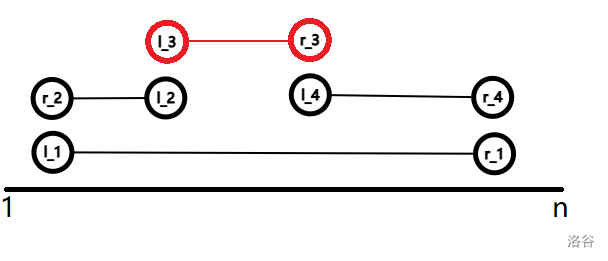
（图中红色的就是 \((u, 2, v, 2)\) 操作）

那么从 \(u\) 点开始一定更优，因为这样就可以使整个强连通分量中的点都变成 \(2\)。那么现在所有情况都讨论完了，于是我们用 \(O(n)\) 的时间复杂度解决了这道题目。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 9;
struct Edge{
	int v, w, nex;
} e[N << 1];
int head[N], ecnt;
void addEdge(int u, int v, int w){
	e[++ecnt] = Edge{v, w, head[u]};
	head[u] = ecnt;
}
struct edge{
	int u, v;
} E[N];
int l[N], r[N], x[N], y[N], beg[N], deg[N], a[N], cnt, tot, n, m, T;
int low[N], dfn[N], scc[N], sc, dfncnt;
stack <int> s;
bool ins[N], vis[N];
vector <int> ans;
void tarjan(int u){
	low[u] = dfn[u] = ++dfncnt;
	s.push(u);
	ins[u] = true;
	for(int i = head[u]; i; i = e[i].nex){
		int &v = e[i].v;
		if(!dfn[v]){
			tarjan(v);
			low[u] = min(low[u], low[v]);
		} else if(ins[v])
			low[u] = min(low[u], dfn[v]);
	}
	if(low[u] == dfn[u]){
		++sc;
		while(s.top() != u){
			scc[s.top()] = sc;
			ins[s.top()] = 0;
			s.pop();
		}
		scc[s.top()] = sc;
		ins[s.top()] = 0;
		s.pop();
	}
}
void dfs(int u){
    vis[u] = true;
    for(int i = head[u]; i; i = e[i].nex){
        int v = e[i].v;
        ans.push_back(e[i].w);
        if(vis[v])
            continue;
        dfs(v);
    }
}
void init(){
    memset(head, 0, sizeof(head));
    memset(beg, 0, sizeof(beg));
    memset(deg, 0, sizeof(deg));
    memset(low, 0, sizeof(low));
    memset(dfn, 0, sizeof(dfn));
    memset(scc, 0, sizeof(scc));
    memset(vis, 0, sizeof(vis));
    memset(a, 0, sizeof(a));
    ans.clear();
    ecnt = cnt = tot = sc = dfncnt = 0;
}
int main(){
    scanf("%d", &T);
    while(T--){
        init();
        scanf("%d%d", &n, &m);
        for(int i = 1; i <= m; i++){
            scanf("%d%d%d%d", &l[i], &x[i], &r[i], &y[i]);
            if(x[i] == 2 && y[i] == 1){
                swap(x[i], y[i]);
                swap(l[i], r[i]);
                E[++tot] = edge{l[i], r[i]};
                addEdge(l[i], r[i], i);
            } else if(x[i] == 1 && y[i] == 2){
                E[++tot] = edge{l[i], r[i]};
                addEdge(l[i], r[i], i);
            } else if(x[i] == 2 && y[i] == 2){
                beg[++cnt] = l[i], beg[++cnt] = r[i];
                ans.push_back(i);
            }
        }
        for(int i = 1; i <= n; i++){
            if(!dfn[i]){
                dfncnt = 0;
                tarjan(i);
            }
        }
        for(int i = 1; i <= tot; i++){
            int u = E[i].u, v = E[i].v;
            if(scc[u] != scc[v])
                deg[scc[v]]++;
        }
        for(int i = 1; i <= cnt; i++)
            if(!deg[scc[beg[i]]] && !vis[beg[i]])
                dfs(beg[i]);
        for(int i = 1; i <= n; i++)
            if(!deg[scc[i]] && !vis[i])
                dfs(i);
        for(int i = 1; i <= m; i++)
            if(x[i] == 1 && y[i] == 1)
                ans.push_back(i);
        for(int i = ans.size() - 1; i >= 0; i--)
            a[l[ans[i]]] = x[ans[i]], a[r[ans[i]]] = y[ans[i]];
        int res = 0;
        for(int i = 1; i <= n; i++)
            res += a[i];
        printf("%d\n", res);
        for(int i = ans.size() - 1; i >= 0; i--)
            printf("%d ", ans[i]);
        printf("\n");
    }
	return 0;
}