题解：P10573 [JRKSJ R8] C0mp0nents

节选自：图论做题记录（三）（2025.5.24 - 2025.31）

特别神秘的题目，难想，但是不好写。

我们首先可以发现，图中只有点权之差的绝对值为 \(k\) 的倍数的点的点权才有可能变成一样的，因此我们可以按 \(\bmod k\) 的值将整张图划分成几个部分，只有每个部分内的边才保留，部分之间的边就可以删掉了。

接下来，我们把所有 \(\bmod ~k\) 同余的点拉出来放在一个序列上，然后我们考虑每一个点 \(s\)。如果 \(t(t > s)\) 这个点的点权最终能变成 \(s\)，那么首先，\(t\) 必须和 \(s\) 连通，其次， \(t\) 必然经历了 \(t \rightarrow t - k \rightarrow t - 2 \times k \rightarrow \dots \rightarrow s\) 的过程，因此 \(s + k\) 必须存在在 \(s\) 处在的连通块中，\(s + 2 \times k\) 必须与 \(s\) 或 \(s + k\) 连边，\(s + 3 \times k\) 必须与 \(s + 2 \times k\)、\(s + k\) 或 \(s\) 连边，以此类推。一旦有一个 \(s + m \times k\) 没有与 \([s, s + (m - 1) \times k]\) 连边，那么比它大的点也就无法通过它作为跳板继续变小了。因此，最终点权能变成 \(s\) 的点必然是一段区间 \([l, r]\)，而根据我们刚才的推导，\([l, r]\) 应该满足以下性质：

• \([l, r]\) 连通；

• 对于所有 \(x \in (s, r)\)，\(x\) 都至少向 \((x, r]\) 中比它大的点连了一条边。

• 对于所有 \(x \in (l, s)\)，\(x\) 都至少向 \((l, x)\) 中比它小的点连了一条边。

如图，此时所有点的权值都可以变成 \(s\)：

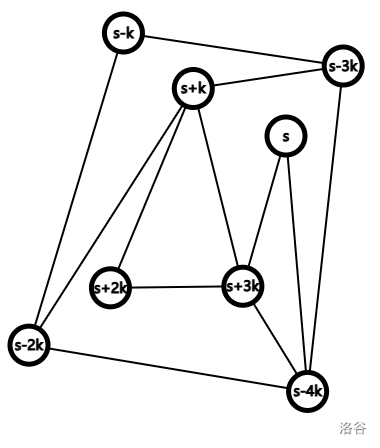
我们先考虑后两个性质。此时我们对于每个 \(s\) 都需要求出最大的 \(rp_s\) 满足 \((s, rp_s]\) 中每个点 \(x\) 都至少与 \((x, rp_s]\) 中的一个点连边。其实我们会发现，当 \(s\) 左移的时候，如果 \(s\) 与 \([s + k, rp_{s + k}]\) 中的点有连边，那么 \(rp_s\) 应该等于 \(rp_{s + k}\)，否则 \(rp_s\) 就应该等于 \(s\)。因此我们处理出与 \(x\) 相连通的点中最大的点 \(r_s\) 与最小的点 \(l_s\)，然后倒着扫一遍就可以了（\(lp_s\) 的意义与求法和 \(rp_s\) 类似，不再赘述）。

此时我们再来考虑第一个性质，根据 \(rp_s\) 和 \(lp_s\) 的定义 \((s, rp_s]\) 中的点以及 \([lp_s, s)\) 中的点已经连通了，我们现在只需要判断 \([lp_s, s)\)、\([s, s]\) 和 \((s, rp_s]\) 是否连通。与 \([s, s]\) 判断连通是容易的，但是有一种情况，\([lp_s, s)\) 和 \((s, rp_s]\) 连边，而 \([lp_s, s)\) 和 \((s, rp_s]\) 中有一个区间与 \([s, s]\) 连边，这也是合法的，此时我们就需要判断两个区间之间是否有连边。显然可以把这两个区间变成二维平面中的两个点，把它们作为对角线上的两个顶点，可以得到一个矩形，我们再把边 \((u, v)\) 也变成二维平面中的一个点，此时只用扫描线数一下这个矩形内有没有点就可以了，不过这样子会带一个 \(\log\)，考虑优化成线性。

我们考虑一条边 \((u, v)\) 会连接哪几个区间，如果 \((u, v)\) 连接了 \([lp_i, s)\) 和 \((s, rp_i]\)，那么一定是如下的情况：

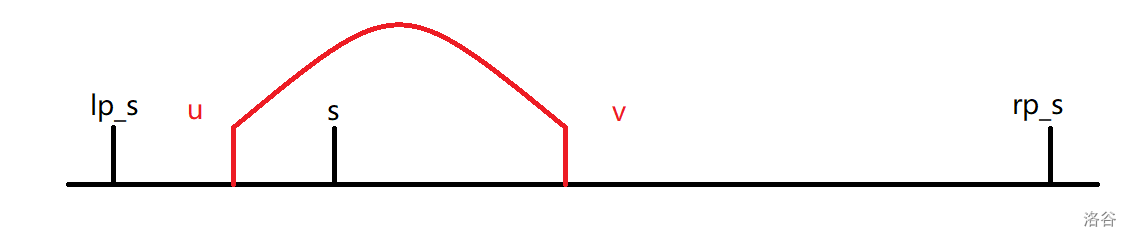
它需要满足 \(lp_s \leq u \leq s \leq v \leq rp_s\)，根据 \(lp_s\) 和 \(rp_s\) 的性质，可以知道它们都是单增的，那么 \((u, v)\) 贡献到的 \(s\) 必然是一段连续的区间。我们设 \(pre_u\) 表示比 \(u\) 小的最大的 \(lp_s\)，\(suf_u\) 表示比 \(u\) 大的最小的 \(rp_s\)，那么一条边 \((u, v)\) 贡献到的 \(s\) 的区间就是 \([\max(u + k, pre_v), \min(v - k, suf_u)]\)，可以用差分处理。

此时就可以对于每一个 \(s\) 判断 \([lp_s, s)\)、\([s, s]\) 和 \((s, rp_s]\) 的连通性了，那么我们就用 \(O(n)\) 的时间复杂度解决了这个问题。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
#define MAXSIZE (1 << 20)
char buf[MAXSIZE], *p1, *p2;
char pbuf[MAXSIZE], *pp;
#define gc() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, MAXSIZE, stdin), p1 == p2) ? EOF : *p1++)
#define pc putchar
inline int read(){
	int x = 0;
	char ch = gc();
	while(!isdigit(ch))
		ch = gc();
	while(isdigit(ch)){
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = gc();
	}
	return x;
}
inline void write(int x){
	if(x > 9)
		write(x / 10);
	putchar(x % 10 + '0');
}
const int N = 4e5 + 9, M = 1e6 + 9, INF = 1e9 + 9;
struct Edge{
    int v, nex;
} e[M << 1];
int head[N], ecnt;
void addEdge(int u, int v){
    e[++ecnt] = Edge{v, head[u]};
    head[u] = ecnt;
}
int n, m, k, ans[N], l[N], r[N], lp[N], rp[N], pre[N], suf[N], sum[N];
int main(){
    n = read();
    m = read();
    k = read();
    for(int i = 1; i <= m; i++){
        int u, v;
        u = read();
        v = read();
        if(u % k == v % k){
            addEdge(u, v);
            addEdge(v, u);
        }
    }
    for(int re = 1; re <= k; re++){
        int tot = n / k + (n % k >= re), up = (tot - 1) * k + re;
        for(int u = re; u <= n; u += k){
            l[u] = -INF, r[u] = INF;
            for(int i = head[u]; i; i = e[i].nex){
                int v = e[i].v;
                if(v < u)
                    l[u] = max(l[u], v);
                else
                    r[u] = min(r[u], v);
            }   
        }
        lp[re] = re;
        for(int i = re + k; i <= n; i += k){
            if(l[i - k] < lp[i - k] && lp[i] != i - k)
                lp[i] = i - k;
            else
                lp[i] = lp[i - k];
        }
        rp[up] = up;
        for(int i = up - k; i >= re; i -= k){
            if(rp[i + k] < r[i + k] && rp[i] != i + k)
                rp[i] = i + k;
            else
                rp[i] = rp[i + k];
        }
        for(int i = re; i <= n; i += k){
            suf[i] = i == re ? i - k : suf[i - k];
            while(suf[i] + k <= n && lp[suf[i] + k] <= i)
                suf[i] += k;
        }
        for(int i = up; i >= re; i -= k){
            pre[i] = i == up ? up + k : pre[i + k];
            while(pre[i] - k >= re && rp[pre[i] - k] >= i)
                pre[i] -= k;
        }
        for(int u = re; u <= n; u += k){
            for(int i = head[u]; i; i = e[i].nex){
                int v = e[i].v;
                if(u >= v)
                    continue;
                int x = max(u + k, pre[v]), y = min(v - k, suf[u]);
                if(x <= y){
                    sum[x]++;
                    sum[y + k]--;
                }
            }
        }
        for(int i = re; i <= n; i += k){
            sum[i] += i == re ? 0 : sum[i - k];
            if(l[i] < lp[i] && rp[i] < r[i])
                lp[i] = rp[i] = i;
            else if(!sum[i]){
                if(l[i] < lp[i])
                    lp[i] = i;
                else if(rp[i] < r[i])
                    rp[i] = i;
            }
            ans[i] = (rp[i] - lp[i] + k) / k;
        }
    }
    for(int i = 1; i <= n; i++){
        write(ans[i]);
        pc(' ');
    }
    return 0;
}