线性代数学习笔记(二):线性基
基本概念
线性基的定义
回顾一下基的概念,空间的一组张成空间为该空间的线性无关的向量组成的集合就被叫做该空间的一组基。用数学语言表示就是对于空间的一组基 \(\hat{u}_1, \hat{u}_2, \hat{u}_3, \dots\),总有 \(v = \displaystyle\sum_{i = 1}^n \lambda_i \hat{u}_i\),且 \(\hat{u}_k \neq \displaystyle\sum_{i = 1 \wedge i \neq k}^n \lambda_i \hat{u}_i\)。
由于信息学与二进制的联系非常大,于是我们考虑将向量的每一位变成 \(0\) 或 \(1\),此时线性组合的操作就变成了异或操作,并且此时一个向量就对应一个数字,此时线性基就可以解决一个子集异或和相关问题,这也是线性基的定义了。
线性基的性质
- 原集合中的任何数都可以用线性基中的一些数异或起来得到;
证明:废话,基的定义中就规定张成空间必须为该空间。
- 线性基中,不存在一组数,使他们的异或和为 \(0\)。
证明:依然是废话,如果 \(x \operatorname{xor} y \operatorname{xor} z \operatorname{xor} \dots = 0\),那么 \(x = y \operatorname{xor} z \operatorname{xor} \dots\),这不符合基的定义中线性无关的规定。
线性基操作与查询
越看越像平衡树
插入
这只是所有线性基构造方法中最普遍的一个,且构造方法十分奇妙。
我们记 \(w_i\) 表示线性基中最高位为 \(i\) 的那一个基,我们规定每个基的二进制位数互不相同,如果存在二进制位数相同的基 \(u, v\),那么把这两个基异或起来,一定会得到一个最高位比它们低的基 \(x\),那么由于 \(x \operatorname{xor} v = u\),我们便不用保留 \(u\) 了,于是线性基一般长这个样子:
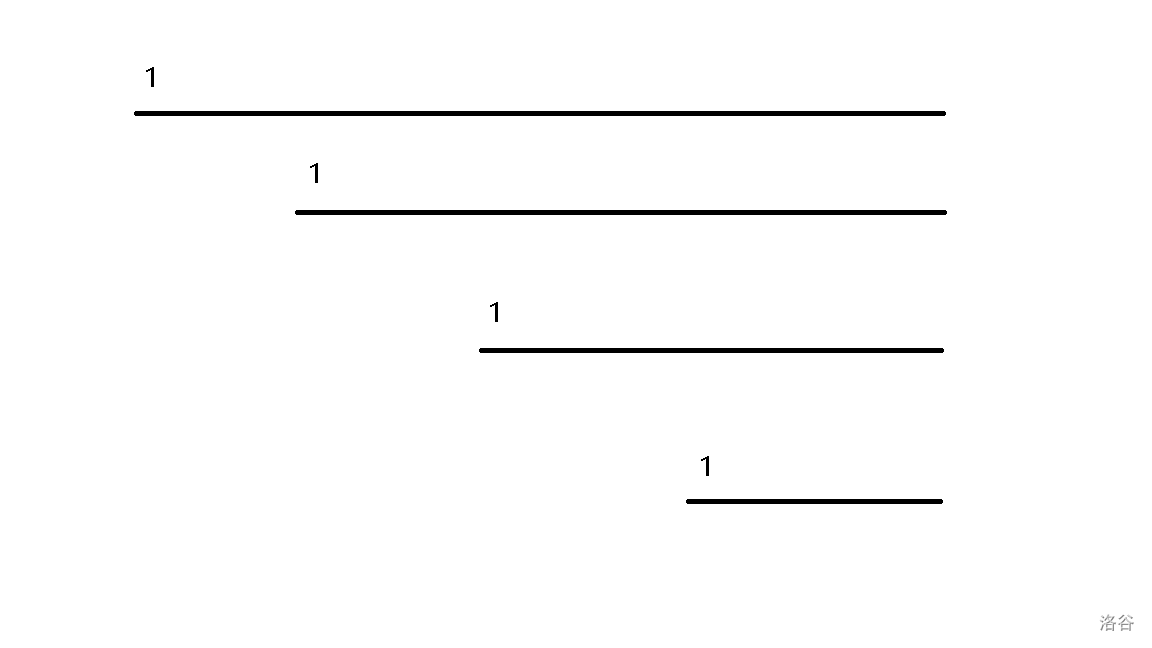
插入操作时,我们不断用 \(x\) 异或当前线性基中的数,如果 \(x\) 的某一位已经被异或为 \(0\) 了,那么用当前的 \(x\) 异或上这个将 \(x\) 的这一位异或成 \(0\) 的那个数,一定就可以将 \(x\) 的这一位又变成 \(0\),于是就跳过。当遇到某个 \(w_i\) 已经没有值的时候,代表 \(x\) 已经无法简化了,直接将 \(x\) 插入即可。
点击查看代码
void insert(int x) {
for(int i = 31; ~i; i--){
if(x >> i & 1){
if(w[i])
x ^= w[i];
else {
w[i] = x;
break;
}
}
}
}
删除
离线做法
这时我们是知道每个数是什么时候被删除的,这时我们记录 \(t_i\) 表示每个数被删除的时间,根据贪心,我们肯定希望在线性基中维护删除时间最晚的元素。考虑线性基的结构,我们希望 \(1\) 位置越高的数越晚被删除。假如 \(x\) 经过若干次异或后与 \(w_i\) 的最高位相同,而 \(x\) 的删除时间比 \(w_i\) 晚,那么 \(x\) 一定是优于 \(w_i\) 的。那么交换一下 \(x\) 与 \(w_i\),把 \(w_i\) 继续往下插入即可。
点击查看代码
void insert(int now, int x){
for(int i = 50; ~i; i--){
if(x >> i & 1){
if(t[i] < now){
swap(t[i], now);
swap(w[i], x);
}
if(!now)
break;
x ^= w[i];
}
}
}
int maxn(int now){
int res;
for(int i = 50; ~i; i--)
if(t[i] > now)
res = max(res, res ^ w[i]);
return res;
}
建议先去看一下例题十一的讲解,然后发现这就是个双倍经验。
我们考虑现在不是找出主路径,而是找到一个主环。其实我们连这个主环都不用找出来,直接把所有的环找出来插入线性基中即可。
我们先把询问离线下来,一个加边操作相当于是加了一个环,一个删边操作相当于删除一个环,将他的删除时间记录下来。对于一个修改操作,可以看做是一次删边操作和一次加边操作。注意,由于这次加边操作是我们构造出来的,不能加到题目的 \(k\) 中,应该将第 \(k\) 条铁路的编号改为一个大于 add 次数的数字。
注意这道题数据大得离谱,有 \(2^{1000}\),直接用 bitset 把值存下来即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e2 + 9, M = 1e3 + 9, INF = 1e9 + 7;
struct Edge{
int v, nex;
bitset <M> w;
} e[N << 1];
int head[N], ecnt;
void addEdge(int u, int v, bitset <M> w){
e[++ecnt] = Edge{v, head[u], w};
head[u] = ecnt;
}
struct edge{
int u, v;
} E[M];
int t[M];
struct Basis{
bitset <M> w[M];
void insert(int now, bitset <M> x){
for(int i = 1000; ~i; i--){
if(x[i]){
if(t[i] < now){
swap(t[i], now);
swap(w[i], x);
}
if(!now)
break;
x ^= w[i];
}
}
}
bitset <M> maxn(int now){
bitset <M> res;
for(int i = 1000; ~i; i--)
if(!res[i] && t[i] > now)
res ^= w[i];
return res;
}
} b;
void print(bitset <M> x){
bool flag = false;
for(int i = 1000; i >= 0; i--){
if(x[i] != 0)
flag = true;
if(flag)
cout << x[i];
}
if(!flag)
cout << 0;
cout << endl;
}
bitset <M> dis[N];
bool vis[N];
void dfs(int u){
vis[u] = true;
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(vis[v])
b.insert(INF, dis[u] ^ dis[v] ^ e[i].w);
else {
dis[v] = dis[u] ^ e[i].w;
dfs(v);
}
}
}
int del[M], id[M], mp[M], n, m, q, cnt, tot;
bitset <M> val[M];
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> m >> q;
cnt = q + 1;
for(int i = 1; i <= m; i++){
int u, v;
string s;
cin >> u >> v >> s;
bitset <M> w(s);
addEdge(u, v, w);
addEdge(v, u, w);
}
dfs(1);
print(b.maxn(0));
for(int i = 1; i <= q; i++){
string s;
cin >> s;
if(s == "Add"){
int u, v;
string s;
cin >> u >> v >> s;
bitset <M> w(s);
id[i] = ++tot;
mp[tot] = tot;
val[tot] = dis[u] ^ dis[v] ^ w;
E[tot] = edge{u, v};
} else if(s == "Cancel"){
int k;
cin >> k;
del[mp[k]] = i;
} else {
int k;
string s;
cin >> k >> s;
bitset <M> z(s);
del[mp[k]] = i;
id[i] = --cnt;
val[cnt] = dis[E[k].u] ^ dis[E[k].v] ^ z;
mp[k] = cnt;
}
}
for(int i = 1; i <= q; i++)
if(!del[i])
del[i] = INF;
for(int i = 1; i <= q; i++){
if(id[i])
b.insert(del[id[i]], val[id[i]]);
print(b.maxn(i));
}
return 0;
}
在线做法
此时我们并不知道每个数是什么时候删除的,因此对于每个集合中的数字,如果它插入线性基失败了,那么就记录一下这个数是用哪几个数异或起来得到的,我们令 \(S\) 表示这些数组成的集合,否则就记录一下这个数异或了哪些后续插入的数,我们令 \(T\) 表示这些数组成的集合。
现在我们要将 \(x\) 从集合中删除,分以下 \(3\) 种情况讨论:
-
\(x\) 未被成功插入线性基中,即它可以被线性基中的数表示出来,此时删除 \(x\) 并未对线性基造成影响,直接删除即可。
-
如果 \(x\) 被成功插入到线性基中,且存在一个数 \(y\) 的 \(S\) 包含 \(x\),则将 \(x\) 从线性基中删去并将 \(y\) 插入线性基中,由于 \(w_1 \operatorname{xor} w_2 \operatorname{xor} w_3 \operatorname{xor} \dots \operatorname{xor} w_{|S| - 1} \operatorname{xor} x = y\),那么 \(w_1 \operatorname{xor} w_2 \operatorname{xor} w_3 \operatorname{xor} \dots \operatorname{xor} w_{|S| - 1} \operatorname{xor} y = x\),因此可以用 \(y\) 异或出 \(x\)。注意消去 \(x\) 后要将所有 \(x\) 所在的集合中的 \(x\) 全部替换为 \(y\).
-
如果 \(x\) 被成功插入到线性基中,但不存在一个数 \(y\) 的 \(S\) 包含 \(x\),此时找到 \(x\) 的 \(T\) 集合并将这个集合中的基全部异或上 \(x\) 即可。
求最大值
由于 \((1\underbrace{00000\dots}_{n 个 0})_2 > (\underbrace{111111\dots}_{n 个 1})_2\),因此我们从高位到低位枚举位数 \(i\),如果 \(ans\) 的第 \(i\) 位为 \(0\),那么直接异或上 \(w_i\) 即可,否则异或 \(w_i\) 就会使 \(ans\) 的最高位变成 \(0\),一定变小了,此时继续往后搜索即可。
点击查看代码
int maxn() {
int res = 0;
for(int i = 31; ~i; i--)
res = max(res, res ^ w[i]);
return res;
}
求 \(k\) 大值
一开始我们构造线性基时,对于 \(u \operatorname{xor} v = x\),我们为了方便操作,我们保留了 \(v\) 和 \(x\),其实,我们也可以保留 \(u\) 和 \(v\),因此线性基不是唯一的,我们可以根据需要选取不同的线性基。
我们考虑求第 \(k\) 小的困难在哪里,就是有些 \(w_i\) 会有好几个二进制位相同,异或时会互相干扰,有些时候两个基异或起来会变大,有些时候两个基异或起来会变小。因此不方便统计,如果我们能把基变成如下形式:
(其中 \(x_i\) 也为二进制下的数,加号表示把两个二进制数拼在一起)
我们设最后化简出了 \(n\) 个基 \(w_1 < w_2 < w_3 < \dots < w_{n - 1} < w_n\),此时最小的能被异或出的数就变成了 \(w_1\),第二小是 \(w_2\),第三小是 \(w_1 \operatorname{xor} w_2\)(此时的 \(\operatorname{xor}\) 不会使两个基异或起来变小这),这时我们发现如果将 \(k\) 二进制表示成了 \((b_0b_1b_2\dots b_{x - 1}b_x)\),那么答案就是 \(\operatorname{xor}_{0 \leq i \leq x} 2^i [b_i = 1]\)。
现在的问题就是要求出这样一组性质优良的基。其实我们可以发现,每个 \(w_i\) 都是所有线性基中 \(w_i\) 最小的,根据这个特性,可以贪心地变化这组线性基。
我们从小到大枚举先前求出的基 \(w_i\),再从大到小枚举 \(j > i\),此时若存在 \(w_i \operatorname{xor} w_j < w_i\),就直接异或掉。我们利用类似数学归纳法的方式证明其正确性。考虑到如果 \(w_i \operatorname{xor} w_j < w_j\),那么一定是 \(w_j\) 的某些位与 \(w_i\) 相同,如果 \(w_i\) 的最高位与 \(w_j\) 的这 \(1\) 位都是 \(1\),那么异或就将 \(1\) 消掉了,否则由于 \(w_i \operatorname{xor} (w_i \operatorname{xor} w_j) = w_j\),因此这个线性基并未发生变化,但是此时就只有 \(w_i\) 在 \(i\) 位置有值了,因此我们就构造成功了。
其实,我们可以再简化一下,如果 \(j > i\) 且 \(j\) 的第 \(i\) 位上都有 \(1\) 此时直接将 \(w_j \operatorname{xor} w_i\) 就可以了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 59;
int n, m;
int w[N], cnt;
struct Basis{
void insert(int x){
for(int i = 55; i >= 0; --i){
if((x >> i) & 1){
if(w[i])
x ^= w[i];
else {
w[i] = x;
break;
}
}
}
}
void build(){
for(int i = 50; i >= 0; --i){
if(!w[i])
continue;
for(int j = i + 1; j <= 50; ++j){
if((w[j] >> i) & 1)
w[j] ^= w[i];
}
}
for(int i = 0; i <= 50; ++i){
if(w[i]){
w[cnt++] = w[i];
}
}
cnt--;
}
int query(int x){
int res = 0;
for(int i = cnt; i >= 0; --i)
if((x >> i) & 1)
res ^= w[i];
return res;
}
} b;
signed main(){
scanf("%lld", &n);
for(int i = 1; i <= n; ++i){
int x;
scanf("%lld", &x);
b.insert(x);
}
b.build();
scanf("%lld", &m);
for(int i = 1; i <= m; i++){
int x;
scanf("%lld", &x);
if(n != cnt + 1)
x--;
if(x >= (1ll << (cnt + 1)))
printf("-1\n");
else
printf("%lld\n", b.query(x));
}
return 0;
}
求 \(k\) 的排名
和树套树时求 \(k\) 的排名一样,套一个二分答案就可以了。
注意到这道题目是一个多重集合,由于我们知道线性基中,不存在一组数,使他们的异或和为 \(0\),那么可以推出,不存在两组数,使它们的异或和相等。那么,假如有 \(tot\) 个数被插入了线性基中,那么插入失败的数就有 \(n - tot\) 个。由于这些数全部可以用线性基表示出来,因此可以用 \(0\) 来表示。由于多少个 \(0\) 异或上一个数还是这个数,因此其实每个数都出现了 \(2^{n - tot}\) 次,那么将最终答案乘以 \(2^{n - tot}\) 即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 59, MOD = 10086;
int n, m;
int w[N], cnt;
int qpow(int a, int b){
int res = 1;
while(b > 0){
if(b & 1)
res = res * a % MOD;
a = a * a % MOD;
b >>= 1;
}
return res;
}
struct Basis{
void insert(int x){
for(int i = 55; i >= 0; --i){
if((x >> i) & 1){
if(w[i])
x ^= w[i];
else {
w[i] = x;
break;
}
}
}
}
void build(){
for(int i = 55; i >= 0; i--){
if(!w[i])
continue;
for(int j = i + 1; j <= 55; j++){
if((w[j] >> i) & 1)
w[j] ^= w[i];
}
}
for(int i = 0; i <= 55; i++){
if(w[i])
w[cnt++] = w[i];
}
cnt--;
}
int query(int x){
int res = 0;
for(int i = cnt; i >= 0; i--)
if((x >> i) & 1)
res ^= w[i];
return res;
}
} b;
signed main(){
scanf("%lld", &n);
for(int i = 1; i <= n; i++){
int x;
scanf("%lld", &x);
b.insert(x);
}
b.build();
int x;
scanf("%lld", &x);
int l = 0, r = (1ll << (cnt + 1)) - 1;//枚举排名
while(l < r){
int mid = (l + r + 1) >> 1;
if(b.query(mid) <= x)
l = mid;
else
r = mid - 1;
}
printf("%lld", (qpow(2, n - cnt - 1) * l + 1) % MOD);
return 0;
}
合并
非常暴力的做法,直接将一个的线性基中每个数字都拿出来,插入另一个线性基中,时间复杂度 \(O(\log^2 n)\)。
看到题目中的异或最大值,第一反应肯定是线性基或 \(01\)Trie,考虑到是求多个数的异或最大值,那么考虑线性基。但这题若用树链剖分维护线性基,复杂度高达 \(O(n \log^4 n)\),必须换一种思路。
考虑类似倍增求 \(LCA\) 的思路,我们记录 \(b_{i, j}\) 表示 \(i\) 到 \(i\) 的 \(j\) 级父亲的线性基合并起来的线性基,转移就是 \(b_{i, j} = b_{i, j - 1} + b_{fa_{i, j - 1}, j - 1}\)(注意此处的 \(+\) 表示线性基合并),求答案时,我们一边求 \(LCA\),一边把线性基合并上去,就可以求出答案了。倍增复杂度为 \(O(\log n)\),线性基合并 \(O(\log^2 n)\),总复杂度就变成了 \(O(n \log^3 n)\),可以有惊无险地通过此题。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e4 + 9;
struct Edge{
int v, nex;
} e[N << 1];
int head[N], ecnt;
void addEdge(int u, int v){
e[++ecnt] = Edge{v, head[u]};
head[u] = ecnt;
}
struct Basis{
int w[69];
Basis(){
memset(w, 0, sizeof(w));
}
void insert(int x){
for(int i = 61; ~i; i--){
if(x >> i & 1){
if(w[i])
x ^= w[i];
else {
w[i] = x;
break;
}
}
}
}
void operator += (Basis a){
for(int i = 61; ~i; i--)
if(a.w[i])
insert(a.w[i]);
}
int maxn(){
int res = 0;
for(int i = 61; ~i; i--)
if(w[i])
res = max(res, res ^ w[i]);
return res;
}
} b[N][19];
int fa[N][19], dep[N], g[N], n, q;
void dfs(int u, int f){
dep[u] = dep[f] + 1;
fa[u][0] = f;
b[u][0].insert(g[u]);
for(int i = 1; i <= 15; i++){
fa[u][i] = fa[fa[u][i - 1]][i - 1];
b[u][i] = b[u][i - 1];
b[u][i] += b[fa[u][i - 1]][i - 1];
}
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(v == f)
continue;
dfs(v, u);
}
}
int query(int x, int y){
Basis res;
if(dep[x] < dep[y])
swap(x, y);
int dis = dep[x] - dep[y];
for(int i = 15; ~i; i--){
if(dis >= (1 << i)){
dis -= (1 << i);
res += b[x][i];
x = fa[x][i];
}
}
if(x == y){
res.insert(g[x]);
return res.maxn();
}
for(int i = 15; ~i; i--){
if(fa[x][i] != fa[y][i]){
res += b[x][i];
res += b[y][i];
x = fa[x][i];
y = fa[y][i];
}
}
res += b[x][0];
res += b[y][0];
res.insert(g[fa[x][0]]);
return res.maxn();
}
signed main(){
scanf("%lld%lld", &n, &q);
for(int i = 1; i <= n; i++)
scanf("%lld", &g[i]);
for(int i = 1; i < n; i++){
int u, v;
scanf("%lld%lld", &u, &v);
addEdge(u, v);
addEdge(v, u);
}
dfs(1, 0);
while(q--){
int x, y;
scanf("%lld%lld", &x, &y);
printf("%lld\n", query(x, y));
}
return 0;
}
线性基的应用
本质不同的异或和个数
我们通过基的性质,推出了线性基的性质二,根据这个性质可以得出一个推论,那就是线性基中不存在两组数,使它们的异或和相等,因为如果存在两组数的异或和相等,他们再异或起来就是 \(0\)。因此线性基中每个子集都可以异或出一个异或和,假设基中有 \(tot\) 个数,那么答案就是 \(2^{tot}\)
观察开关的性质,发现他可以将关的灯打开,开的灯关上,也就是让 \(0\) 变成 \(1\),\(1\) 变成 \(0\),这正好可以用 \(\operatorname{xor} 1\) 实现。于是把每个开关控制的灯设为 \(1\),没有控制的设为 \(0\),得到 \(m\) 个二进制数,直接把它们插入线性基中,然后查询异或和个数即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 59, MOD = 2008;
int n, m, cnt;
char s[N];
struct Basis{
int w[N];
Basis(){
memset(w, 0, sizeof(w));
}
void insert(int x){
for(int i = 55; i >= 0; --i){
if((x >> i) & 1){
if(w[i])
x ^= w[i];
else {
if(x != 0)
cnt++;
w[i] = x;
break;
}
}
}
}
} b;
signed main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i++){
scanf("%s", s + 1);
int x = 0;
for(int i = 1; i <= n; i++)
x = (x << 1) + (s[i] == 'O');
b.insert(x);
}
printf("%d", (1ll << cnt) % MOD);
return 0;
}
本质不同的异或和的和
现在看线性基又像线段树单侧递归:前缀最大值个数、前缀最大值的和。
由于线性基中任意一组基异或起来都互不相同,这大大简化了这个问题,我们只需要统计即可,不需要考虑去重。
我们考虑按位算贡献。假设线性基中有 \(tot\) 个基,其中有 \(k (k > 0)\) 个基的第 \(i\) 位为 \(1\),那么就有 \(tot - k\) 个第 \(i\) 位为 \(0\) 的基。这些第 \(i\) 位为 \(0\) 的基无论选不选都对答案不造成贡献,因此最终这一位的答案一定会乘以 \(2^{tot - k}\)。
现在我们考虑第 \(i\) 位为 \(1\) 的 \(k\) 个基,只有当从中选出奇数个基时,才会在这一位上留下一个 \(1\),因此答案是 \(\displaystyle\sum_{0 \leq j \leq k \wedge j \bmod 2 = 1} \binom kj\)。
我们考虑二项式定理 \((x + y)^k = \displaystyle\sum_{0 \leq j \leq k} \binom kj x^j y^{k - j}\),由于 \(k > 0\),我们把 \(x, y\) 带成 \(-1\) 和 \(1\),那么 \(0 = \displaystyle\sum_{0 \leq j \leq k} \binom kj (-1)^j\),这个式子在 \(j\) 为偶数时为正,\(j\) 为奇数时为负,于是 \(\displaystyle\sum_{0 \leq j \leq k \wedge j \bmod 2 = 1} \binom kj = \sum_{0 \leq j \leq k \wedge j \bmod 2 = 0} \binom kj\)。
因为组合数一行之和 \(\displaystyle 2^k\),那么 \(\displaystyle\sum_{0 \leq j \leq k \wedge j \bmod 2 = 1} \binom kj = 2^{k - 1}\),于是这一位的答案就是 \(2^{tot - 1}\)。
很显然,如果 \(k\) 为 \(0\) 那么答案就是 \(0\),因此如果存在一个最高位为 \(i\) 的基,那么答案就会乘以 \(2^{tot - 1}\),那么答案就是 \(\displaystyle\prod_{i = 0}^{\log n} 2^{tot - 1} [w_i \neq 0]\)。
回到这道题目,我们需要求不同的路径异或和的和。参考例题十一,我们把所有环插入线性基中,再找到一条主路径,那么最终答案就是线性基中的答案异或上主路径长度,但 \(u\) 和 \(v\) 都是不固定的,如果一对一对枚举,复杂度直接炸了,考虑如何优化。
还是考虑异或相等为 \(0\) 的情况。如果我们随便找一个点作为起点,记录到 \(u\) 的距离 \(dis_u\) 和到 \(v\) 的距离 \(dis_v\),那么 \(u\) 到 \(v\) 的距离就是 \(dis_u \operatorname{xor} dis_v\)。
那么现在问题就变成了在集合 \(\{dis_i\}\),中任意选两个数字 \(dis_u, dis_v\),我们求出线性基中异或和的和,再异或上 \(dis_u\) 和 \(dis_v\),加入到答案中就行了。但这样复杂度依然爆炸。
我们继续考虑按位贡献,我们知道线性基如果有一个数第 \(i\) 位上是 \(1\),那么这一位上就有 \(2^{tot - 1}\) 种方式凑出 \(1\),\(2^{tot - 1}\) 种方式凑出 \(0\)。因此无论 \(\{dis_i\}\) 中选出两个数的异或和的第 \(i\) 位为 \(1\) 或者 \(0\),对答案的贡献都是 \(2^{tot - 1}\)。假设 \(\{dis_i\}\) 的大小为 \(siz\),那么总贡献就是 \(2^{tot - 1} \times \displaystyle\frac{siz(siz - 1)}{2}\)。
如果线性基中没有数字第 \(i\) 位上是 \(1\),那么无论多少个数异或起来都是 \(0\),因此答案需要乘以 \(2^{tot}\)。其次选出的 \(dis_u\) 和 \(dis_v\) 的第 \(i\) 位上必须一个是 \(0\),一个是 \(1\)。我们假设 \(\{dis_i\}\) 中有 \(cnt\) 个数字第 \(i\) 位上为 \(1\),那么对于答案的贡献就是 \(2^{tot} \times cnt \times (siz - cnt)\)。
最后,这道题的图可能不联通,每个连通块分开算即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 9, M = 2e5 + 9, MOD = 1e9 + 7;
struct Edge{
int v, w, nex;
} e[M << 1];
int head[N], ecnt;
void addEdge(int u, int v, int w){
e[++ecnt] = Edge{v, w, head[u]};
head[u] = ecnt;
}
int qpow(int a, int b){
int res = 1;
while(b > 0){
if(b & 1)
res = res * a % MOD;
a = a * a % MOD;
b >>= 1;
}
return res;
}
int dis[N], n, m, ans, sum;
vector <int> vec;
bool vis[N];
struct Basis{
int w[69], tot;
void clear(){
memset(w, 0, sizeof(w));
tot = 0;
}
void insert(int x){
for(int i = 62; ~i; i--){
if(x >> i & 1ll){
if(w[i])
x ^= w[i];
else {
w[i] = x;
tot++;
break;
}
}
}
}
int calc(){
int sum = 0, res = 0, siz = vec.size();
for(int i = 62; ~i; i--)
sum |= w[i];
for(int i = 62; ~i; i--){
int cnt = 0;
for(int j = 0; j < siz; j++)
if(vec[j] >> i & 1ll)
cnt++;
if(sum >> i & 1ll)
res = (res + qpow(2, i) % MOD * qpow(2, tot - 1) % MOD * (siz * (siz - 1) / 2 % MOD) % MOD) % MOD;
else
res = (res + qpow(2, i) % MOD * qpow(2, tot) % MOD * cnt % MOD * (siz - cnt) % MOD) % MOD;
}
return res;
}
} b;
void dfs(int u){
vis[u] = true;
vec.push_back(dis[u]);
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(vis[v])
b.insert(dis[u] ^ dis[v] ^ e[i].w);
else {
dis[v] = dis[u] ^ e[i].w;
dfs(v);
}
}
}
signed main(){
scanf("%lld%lld", &n, &m);
for(int i = 1; i <= m; i++){
int u, v, w;
scanf("%lld%lld%lld", &u, &v, &w);
addEdge(u, v, w);
addEdge(v, u, w);
}
for(int i = 1; i <= n; i++){
if(!vis[i]){
b.clear();
vec.clear();
dfs(i);
ans = (ans + b.calc()) % MOD;
}
}
printf("%lld", ans);
return 0;
}
贪心
线性基已经可以求出异或最大值了,那么线性基上的贪心一般是求带异或限制的最值问题。
首先,由于“一个矿石组合会产生“魔法抵消”当且仅当存在一个非空子集,那些矿石的元素序号按位异或起来为零”,那么选出的矿石元素序号一定构成一组线性基。
考虑把所有矿石元素序号 \(x\) 插入线性基,如果插入失败了,那么一定有 \(x = \operatorname{xor}_i w_i\),于是线性基中任意一个 \(w_i = x \operatorname{xor}_{j \neq i} w_j\)。考虑本题需要选出的矿石的魔力值和最大,于是如果 \(x\) 的魔力值比某个基大,那么直接用 \(x\) 将其替换即可。
其实,我们直接按魔力值从大到小将序号能插入就插入线性基中,那么一定不会发生魔力值的替换。最后直接输出基中魔力值的和即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e3 + 9;
int n;
struct Basis{
int w[69];
bool insert(int x){
for(int i = 64; i >= 0; --i){
if((x >> i) & 1){
if(w[i])
x ^= w[i];
else {
w[i] = x;
return true;
}
}
}
return false;
}
} b;
struct Element{
int num, mag;
} e[N];
bool cmp(Element a, Element b){
if(a.mag == b.mag)
return a.num < b.num;
return a.mag > b.mag;
}
int ans;
signed main(){
scanf("%lld", &n);
for(int i = 1; i <= n; i++)
scanf("%lld%lld", &e[i].num, &e[i].mag);
sort(e + 1, e + n + 1, cmp);
for(int i = 1; i <= n; i++)
if(b.insert(e[i].num))
ans += e[i].mag;
printf("%lld", ans);
return 0;
}
考虑朴素的 Nim 游戏,先手必胜当且仅当所有石子堆大小的异或和不为 \(0\),于是先手必须去掉一些石子堆,使得剩下的石子堆集合的所有非空子集的异或和都不为 \(0\),而线性基正好满足这个性质。
那么现在问题就变成了选出一些数使得它们可以构成线性基,且它们的石子和最大,那么这道题目就直接变成上一道题目了,那么这道题就做完了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e3 + 9;
int a[N], n, ans;
bool flag;
struct Basis{
int w[69];
bool insert(int x){
for(int i = 64; i >= 0; --i){
if((x >> i) & 1){
if(w[i])
x ^= w[i];
else {
w[i] = x;
return true;
}
}
}
return false;
}
} b;
signed main(){
scanf("%lld", &n);
for(int i = 1; i <= n; i++)
scanf("%lld", &a[i]);
sort(a + 1, a + n + 1);
for(int i = n; i >= 1; i--)
if(!b.insert(a[i])){
ans += a[i];
flag = true;
}
printf("%lld", flag ? ans : -1);
return 0;
}
这个题目和例题八很像,只是此时线性基不再是二进制数字了,而是变成了一个向量。
类似地,我们不断用线性基中的向量将插入的向量 \(v\) 的最高位消掉,如果某一时刻 \(v\) 变成 \(0\) 向量了,那么这个时候 \(v\) 就可以被基中的数字线性表示,否则将 \(v\) 插入线性基。
其他就和例题八一样了,按价格从小到大不断插入线性基中,如果插入成功就更新答案,然后就做完了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 509;
const double eps = 1e-4;
struct Equipment{
double a[N];
int c;
} e[N];
bool cmp(Equipment x, Equipment y){
return x.c < y.c;
}
int tmp[N], ans1, ans2, n, m;
struct Basis{
double w[N][N];
bool insert(double *x){
for(int i = m; i >= 1; i--){
if(fabs(x[i]) > eps){
if(!w[i][i]){
for(int j = i; j >= 1; j--)
w[i][j] = x[j];
return true;
} else {
double tmp = x[i] / w[i][i];
for(int j = i; j >= 1; j--)
x[j] -= tmp * w[i][j];
}
}
}
return false;
}
} b;
signed main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
scanf("%lf", &e[i].a[j]);
for(int i = 1; i <= n; i++)
scanf("%d", &e[i].c);
sort(e + 1, e + n + 1, cmp);
for(int i = 1; i <= n; i++){
if(b.insert(e[i].a)){
ans1++;
ans2 += e[i].c;
}
}
printf("%d %d", ans1, ans2);
return 0;
}
图论
我们考虑先随便找到一条 \(1\) 到 \(n\) 的路径(可能不是最优秀的),我们现在要将其变成最优的。可以发现肯定是这条路径上支出去了支路,从走一段支路又回到了主路径,比如下图中红、蓝、绿三条路径:
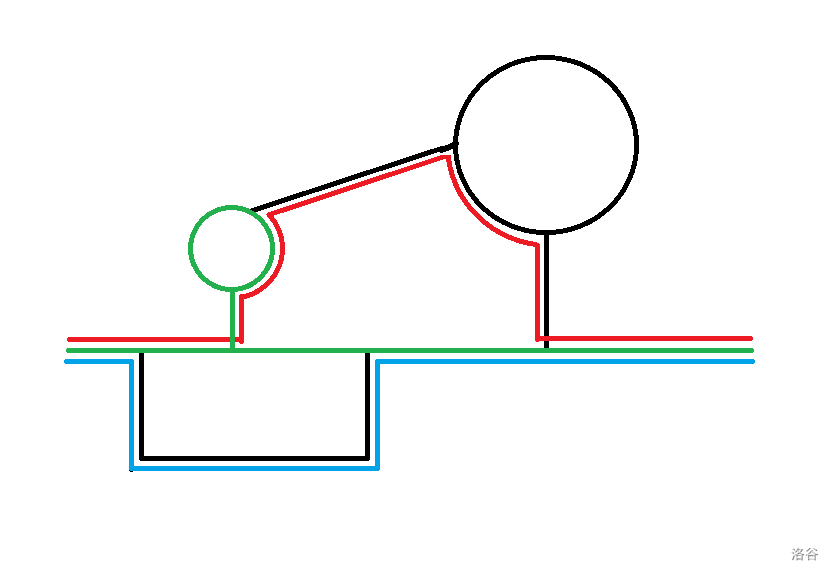
当我们把这三条路径都异或上主路径后,由于异或相同为 \(0\),不同为 \(1\) 的优良性质,这张图就变成了这个样子:
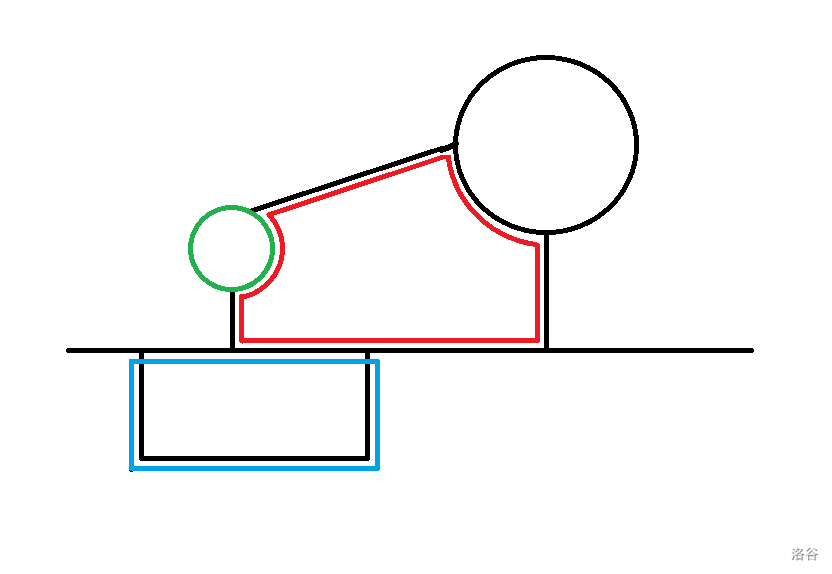
(由于主路径走到绿色的环上后还要走回来,因此竖着的绿色直线要走两次,依然也被异或掉了)
可以发现这些支路都变成了环,用主路径异或上任意若干个还就可以得到任意一条其他路径。因此,我们找到所有从 \(1\) 出发可以到达的环,把它们全部插入线性基中,再查询与主路径异或起来的最大值就行了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e4 + 9, M = 1e5 + 9;
struct Edge{
int v, w, nex;
} e[M << 1];
int head[N], ecnt;
void addEdge(int u, int v, int w){
e[++ecnt] = Edge{v, w, head[u]};
head[u] = ecnt;
}
struct Basis{
int w[69];
Basis(){
memset(w, 0, sizeof(w));
}
void insert(int x){
for(int i = 63; ~i; i--){
if(x >> i & 1){
if(w[i])
x ^= w[i];
else {
w[i] = x;
break;
}
}
}
}
int maxn(int x){
int res = x;
for(int i = 63; ~i; i--)
res = max(res, res ^ w[i]);
return res;
}
} b;
int n, m;
int dis[N];
bool vis[N];
void dfs(int u){
vis[u] = true;
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(vis[v])
b.insert(dis[u] ^ dis[v] ^ e[i].w);
else {
dis[v] = dis[u] ^ e[i].w;
dfs(v);
}
}
}
signed main(){
scanf("%lld%lld", &n, &m);
for(int i = 1; i <= m; i++){
int u, v, w;
scanf("%lld%lld%lld", &u, &v, &w);
addEdge(u, v, w);
addEdge(v, u, w);
}
dfs(1);
printf("%lld\n", b.maxn(dis[n]));
return 0;
}
和上一道题目很像,只不过变成了最小值,于是我们先按照求第 \(k\) 小的思路将线性基重建,此时线性基中只有最高位和 \(dis_n\) 一样的那个基可以使其变小,因此我们只需要不断找到那个基就可以了,其实可以全部扫一遍,如果异或值更小就更新,然后就做完了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 9;
struct Edge{
int v, w, nex;
} e[N << 1];
int head[N], ecnt;
void addEdge(int u, int v, int w){
e[++ecnt] = Edge{v, w, head[u]};
head[u] = ecnt;
}
struct Basis{
int w[69], cnt;
Basis(){
memset(w, 0, sizeof(w));
}
void insert(int x){
for(int i = 63; ~i; i--){
if(x >> i & 1){
if(w[i])
x ^= w[i];
else {
w[i] = x;
break;
}
}
}
}
void build(){
for(int i = 63; i >= 0; --i){
if(!w[i])
continue;
for(int j = i + 1; j <= 63; ++j){
if((w[j] >> i) & 1)
w[j] ^= w[i];
}
}
for(int i = 0; i <= 63; ++i)
if(w[i])
w[cnt++] = w[i];
cnt--;
}
int query(int x){
int res = x;
for(int i = cnt; i >= 0; --i)
res = min(res, res ^ w[i]);
return res;
}
} b;
int n, m;
int dis[N];
bool vis[N];
void dfs(int u){
vis[u] = true;
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(vis[v])
b.insert(dis[u] ^ dis[v] ^ e[i].w);
else {
dis[v] = dis[u] ^ e[i].w;
dfs(v);
}
}
}
signed main(){
scanf("%lld%lld", &n, &m);
for(int i = 1; i <= m; i++){
int u, v, w;
scanf("%lld%lld%lld", &u, &v, &w);
addEdge(u, v, w);
addEdge(v, u, w);
}
dfs(1);
b.build();
printf("%lld\n", b.query(dis[n]));
return 0;
}
线性基区间操作
我们把线性基的诸多操作搬到序列上,就可以处理某些序列上异或操作与异或查询的问题,先来看一道静态的题目。
此时就要用到大名鼎鼎的可持久化线性基。
其实这也不是什么高大上的东西,就是每次复制一遍上一次的线性基,在复制后的线性基上改就行了。
我们求出所有可持久化线性基前缀线性基,然后对于同一个数字,它要么不选,要么只会选 \(1\) 个,因为选多会因为异或抵消掉。如果要选这个数字,我们选区间内任意一个皆可,但我们希望能让更多的区间可以选这个数,因此我们在插入线性基时,我们和可删除线性基一样,记录一下线性基中每个基最后出现的位置,如果当前插入的 \(x\) 与 \(w_i\) 的最高位都是 \(1\),但是 \(x\) 出现的位置比 \(w_i\) 靠后,那么就把 \(w_i\) 替换为 \(x\),把原来的 \(w_i\) 继续往下插入即可。
查询时,找到对应的线性基,像可删除线性基一样查询即可。
忽然反应过来,这个东西可以有个更高大上的名字:带删除可持久化线性基。
其实也可以离线下来跑一遍。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 9;
struct Basis{
int w[32], t[32];
Basis(){
memset(w, 0, sizeof(w));
memset(t, 0, sizeof(t));
}
void insert(int now, int x){
for(int i = 31; ~i; i--){
if(x >> i & 1){
if(t[i] < now){
swap(t[i], now);
swap(w[i], x);
}
if(!now)
break;
x ^= w[i];
}
}
}
int maxn(int now){
int res = 0;
for(int i = 31; ~i; i--)
if(w[i] && t[i] >= now)
res = max(res, res ^ w[i]);
return res;
}
} b[N];
int a[N], n, q;
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%d", &a[i]);
b[i] = b[i - 1];
b[i].insert(i, a[i]);
}
scanf("%d", &q);
while(q--){
int l, r;
scanf("%d%d", &l, &r);
printf("%d\n", b[r].maxn(l));
}
return 0;
}
这道题目现在变成动态的了,
参考资料
-
黄yy、张hr 的课件
-
线性基学习笔记 Troverld
-
关于带删除线性基 lnzwz
-
题解 P3733 【[HAOI2017]八纵八横】 xtx1092515503
-
线性基 花花の水晶植轮daisuki
-
线性基求第k小异或值 hjmmm
本文来自博客园,作者:Orange_new,转载请注明原文链接:https://www.cnblogs.com/JPGOJCZX/p/18777540


 浙公网安备 33010602011771号
浙公网安备 33010602011771号