题解:CF1340F Nastya and CBS
连毒瘤都觉得毒瘤的题,对于我这种凡人来说,真的是一坨超级大的,写加调一共花了 \(6\) 天 qwq。
依然考虑用线段树单侧递归解决这道题目,我们令线段树上一个节点 \([l, r]\) 维护这段括号序列未匹配的括号信息。如果一个节点出现了 \((]\) 这种情况,那么无论后面拼上什么括号序列,都无法将其消除,直接打上一个标记即可。同时,我们也知道了,如果一个节点维护的未匹配括号能在以后被匹配上,那么一定是一段右括号加一段左括号的形式:\()\}>)])] ((\{<[(<\)。
依然考虑单侧递归的形式,我们现在要将 \(id\) 的左儿子和 \(id\) 的右儿子的信息合并到 \(id\)。显然,如果一个节点被标记了,那么直接将 \(id\) 也打上标记即可。
现在我们考虑一般情况,我们希望 \(id\) 的左儿子的左括号能与 \(id\) 的右儿子的右括号相匹配,这不难想到哈希,于是我们在线段树一个节点要记录左括号个数、左括号哈希值、右括号个数、右括号哈希值这 \(4\) 个信息。
这里顺道讲一下我的哈希方法,由于传统模数 \(998244353\) 与 \(10^9 + 7\) 太容易被卡,且取模速度极慢,于是我们换一个模数 \(p = 2^{61} - 1\)(是个质数)。可以发现,\(2^{61} - 1\) 的所有 \(61\) 个二进制位都是 \(1\),那么对于被取模数 \(x\) 的后 \(61\) 位,取模后还是其本身,因此就是 \((2^{61} - 1) \operatorname{and} x\),而剩下的那些位可以写成 \(y \times 2^{61}\),我们考虑对其做带余除法:\(\displaystyle\frac{y \times 2^{61}}{2^{61} - 1} = \frac{y \times (2^{61} - 1) + y}{2^{61} - 1} = \frac{y}{2^{61} - 1}\)。于是直接右移 \(61\) 位,加上 \((2^{61} - 1) \operatorname{and} x\),再取模就行了(其实可以直接减)。
说回正题,假设现在 \(id\) 的左儿子的左括号数大于 \(id\) 的右儿子的右括号数(对称情况同理),那么我们现在需要找到 \(id\) 的左儿子的左括号的一段后缀与 \(id\) 的右儿子的右括号进行匹配,我们令 \(now\) 表示目前递归到节点 \(now\),\(ls\) 表示 \(now\) 的左儿子,\(rs\) 表示 \(now\) 的右儿子,\(sum\) 还需要匹配 \(sum\) 个右括号。初始时 \(now\) 为 \(id\) 的左儿子,\(sum\) 为 \(id\) 的右儿子的右括号数。
-
如果 \(rs\) 的左括号数等于 \(sum\),直接返回这段左括号的哈希值;
-
如果 \(rs\) 的左括号数大于 \(sum\),直接往 \(rs\) 递归即可。
现在我们来考虑最复杂的 \(rs\) 的左括号数小于 \(sum\) 的情况,那么 \(now\) 的左括号的来源应该如图:
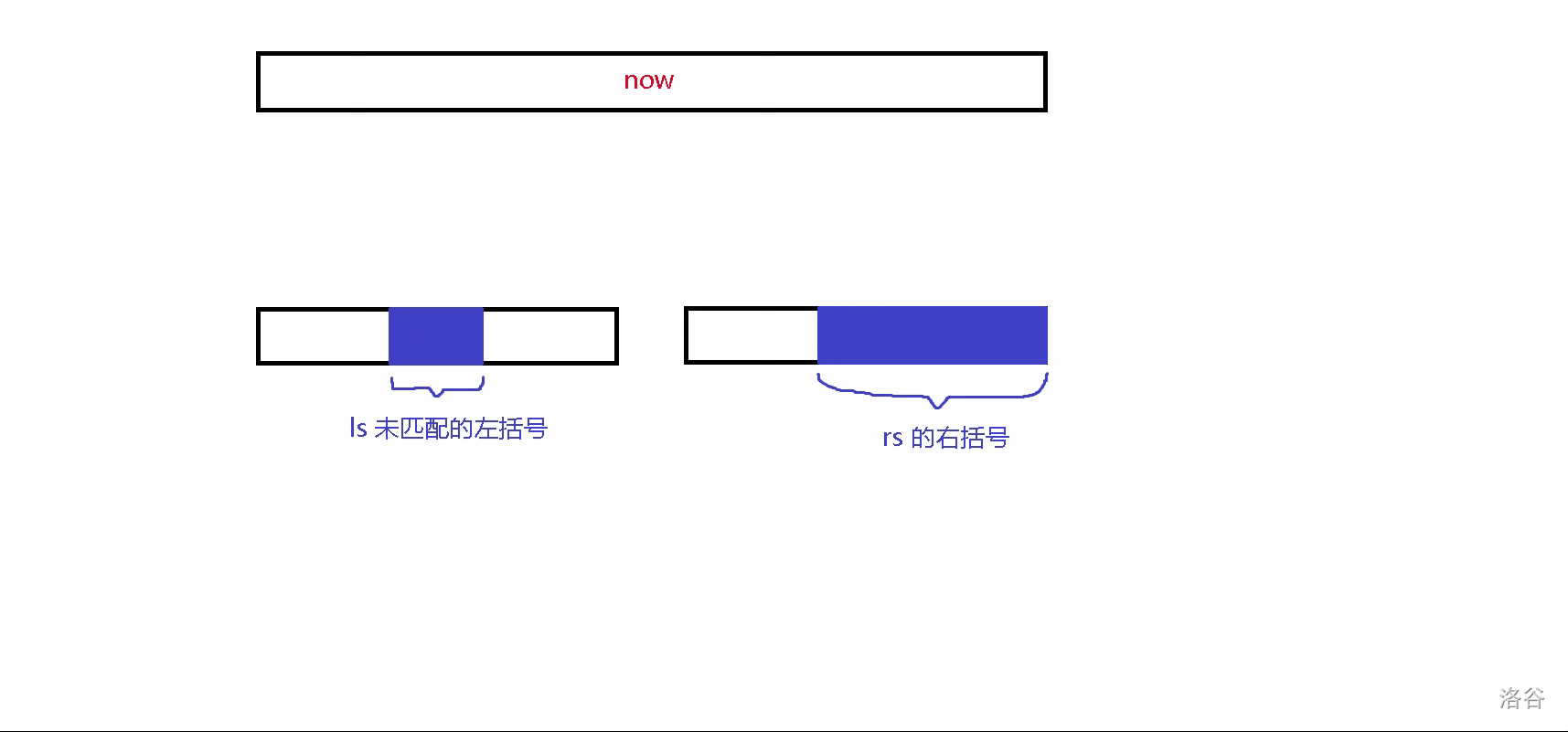
\(rs\) 的左括号的哈希值是好求的,我们考虑 \(ls\) 的左括号的哈希值。这个值等于 \(ls\) 所有左括号的哈希值减去发生匹配的左括号的哈希值,而发生匹配的左括号的哈希值正好等于 \(rs\) 的右括号的哈希值:
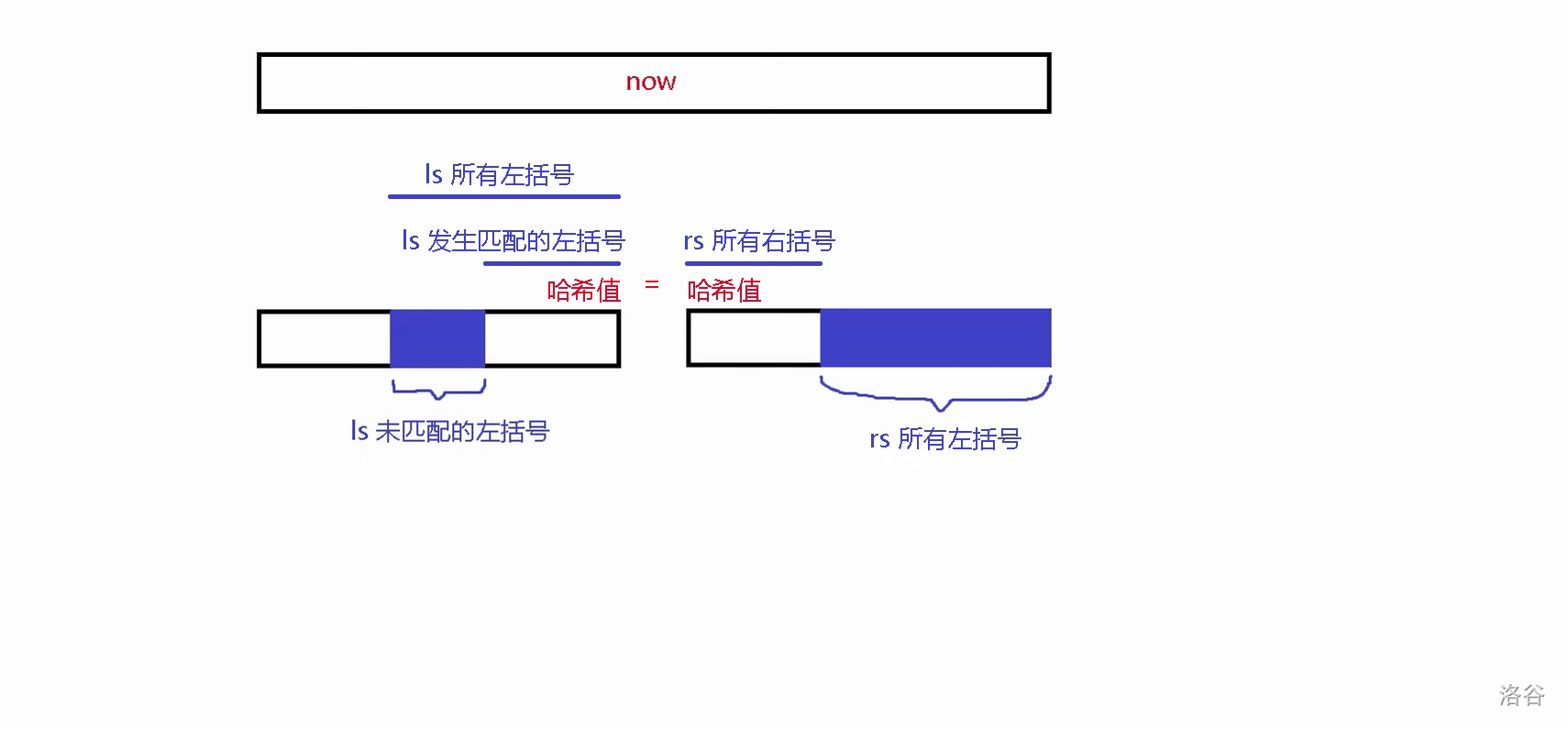
于是,我们将返回值加上 \(rs\) 左括号的哈希值,再减去 \(rs\) 右括号的哈希值,往 \(ls\) 递归即可。
注意此处的加减均为哈希值的加减,注意顺序和基数。
query 操作和合并操作类似,我们把找出来的 \(cnt = O(\log_2 n)\) 个节点重新建成一棵“左偏”的线段树(不需要正真建出来,从左往右扫一遍即可):
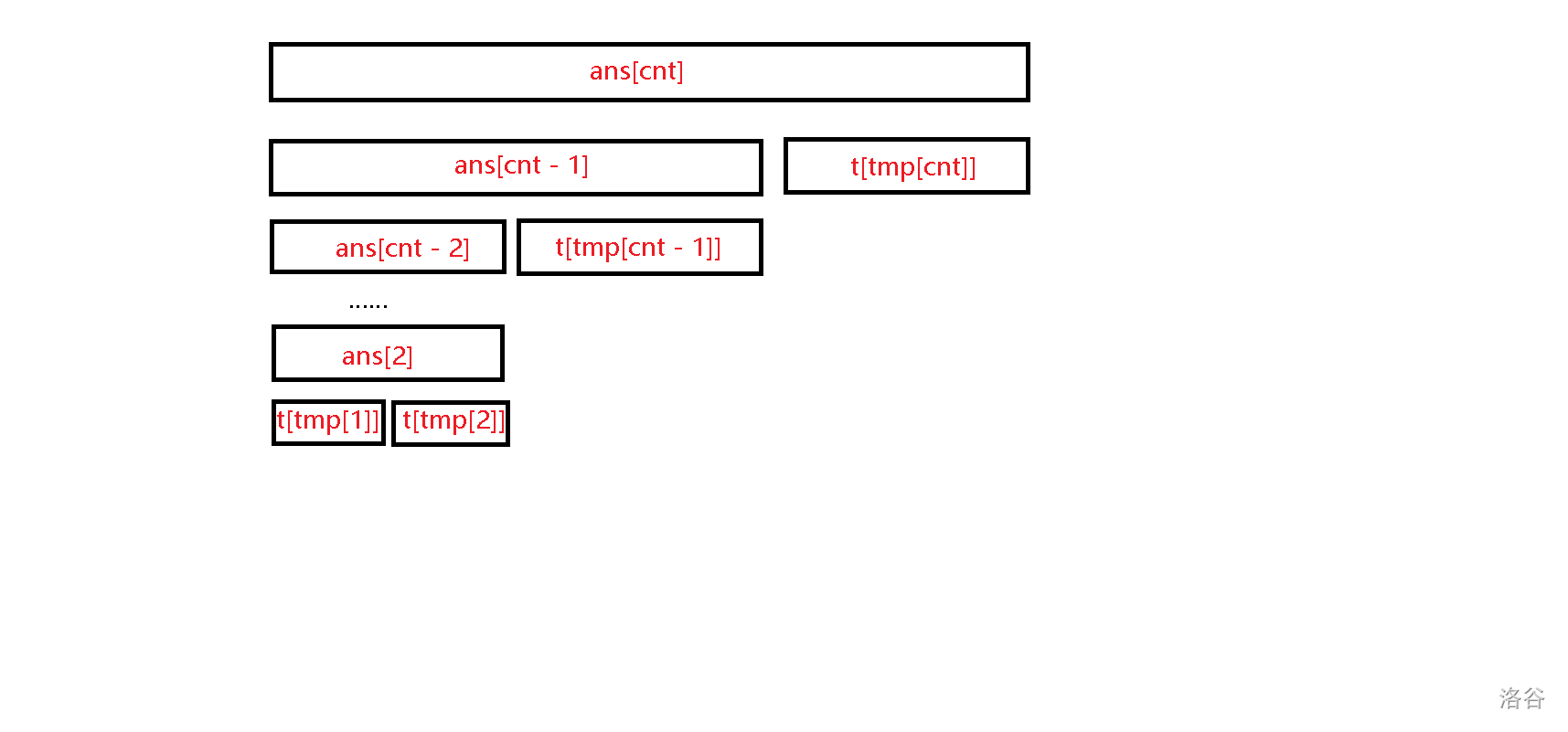
(ans[i] 记录前 \(i\) 个节点匹配后的括号序列,tmp[i] 记录第 \(i\) 个节点在原线段树上的编号)
单侧递归时,如果往左儿子走,那么与合并时往左儿子走类似,否则就是在原线段树上某个节点找其右儿子的一段后缀与需要的左括号相匹配,直接调用之前编好的函数即可,于是我们在 \(O(n \log^2 n)\) 的时间复杂度内解决了这个问题。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 9, base = 5201314, MOD = (1ll << 61) - 1;
int B[N], n, k, q;
int plu(int x, int y){
return x + y > MOD ? x + y - MOD : x + y;
}
int sub(int x, int y){
return x < y ? x - y + MOD : x - y;
}
int mod(__int128 x){
return sub((MOD & x) + (x >> 61), MOD);
}
int mul(__int128 x, int y){
return mod(x * y);
}
struct Hash{
int len, val;
Hash(){
len = val = 0;
}
Hash operator + (const Hash &b) const{//将 b 拼在 a 的右边 a + b = ab
Hash res;
res.val = plu(mul(b.val, B[len]), val);
res.len = len + b.len;
return res;
}
Hash operator - (const Hash &b) const{//将 a 开头 b 个字母去掉 ab - b = a
Hash res;
res.val = sub(val, mul(b.val, B[len - b.len]));
res.len = len - b.len;
return res;
}
};
struct Sgt{
Hash l, r;//右括号在左边,左括号在右边 )}>)])] (({<[(<
bool flag;
} t[N << 2];
Hash getval1(int now, int sum){//目前在节点 now,需要凑 sum 个左括号
if(sum == 0)
return Hash();
if(t[now].l.len == sum)//当前节点恰好有 sum 个左括号
return t[now].l;
else if(t[now << 1 | 1].l.len > sum)//当前节点右儿子有 >sum 个左括号
return getval1(now << 1 | 1, sum);//往右儿子递归
else
return getval1(now << 1, sum - t[now << 1 | 1].l.len + t[now << 1 | 1].r.len) - t[now << 1 | 1].r + t[now << 1 | 1].l;
}
Hash getval2(int now, int sum){//目前在节点 now,需要凑 sum 个右括号,与 getval1 同理
if(sum == 0)
return Hash();
if(t[now].r.len == sum)
return t[now].r;
else if(t[now << 1].r.len > sum)
return getval2(now << 1, sum);
else {
return getval2(now << 1 | 1, sum - t[now << 1].r.len + t[now << 1].l.len) - t[now << 1].l + t[now << 1].r;
}
}
void pushup(int id){
if(t[id << 1].flag || t[id << 1 | 1].flag)
return t[id].flag = 1, void();
t[id].flag = 0;
if(t[id << 1].l.len > t[id << 1 | 1].r.len){//在左儿子找与右儿子匹配的括号
if(getval1(id << 1, t[id << 1 | 1].r.len).val == t[id << 1 | 1].r.val){
t[id].r = t[id << 1].r;
t[id].l = t[id << 1].l - t[id << 1 | 1].r + t[id << 1 | 1].l;
} else
t[id].flag = true;
} else {//同理
if(getval2(id << 1 | 1, t[id << 1].l.len).val == t[id << 1].l.val){
t[id].l = t[id << 1 | 1].l;
t[id].r = t[id << 1 | 1].r - t[id << 1].l + t[id << 1].r;
} else
t[id].flag = true;
}
}
void build(int id, int l, int r){
if(l == r){
int tmp;
scanf("%lld", &tmp);
if(tmp > 0){
t[id].l.val = tmp;
t[id].l.len = 1;
} else {
t[id].r.val = -tmp;
t[id].r.len = 1;
}
return;
}
int mid = (l + r) >> 1;
build(id << 1, l, mid);
build(id << 1 | 1, mid + 1, r);
pushup(id);
}
void modify(int id, int l, int r, int q, int qx){
if(l == r){
if(qx > 0){
t[id].l.val = qx;
t[id].r.val = 0;
t[id].l.len = 1;
t[id].r.len = 0;
} else {
t[id].r.val = -qx;
t[id].l.val = 0;
t[id].r.len = 1;
t[id].l.len = 0;
}
return;
}
int mid = (l + r) >> 1;
if(q <= mid)
modify(id << 1, l, mid, q, qx);
else
modify(id << 1 | 1, mid + 1, r, q, qx);
pushup(id);
}
int sta[N], cnt;
void query(int id, int l, int r, int ql, int qr){
if(ql <= l && r <= qr)
return sta[++cnt] = id, void();
int mid = (l + r) >> 1;
if(ql <= mid)
query(id << 1, l, mid, ql, qr);
if(qr > mid)
query(id << 1 | 1, mid + 1, r, ql, qr);
}
Sgt ans[N];
Hash getval3(int now, int sum){
if(sum == 0)
return Hash();
if(ans[now].l.len == sum)
return ans[now].l;
else if(t[sta[now]].l.len > sum)
return getval1(sta[now], sum);
else
return getval3(now - 1, sum - t[sta[now]].l.len + t[sta[now]].r.len) - t[sta[now]].r + t[sta[now]].l;
}
signed main(){
scanf("%lld%lld", &n, &k);
B[0] = 1;
for(int i = 1; i <= n; i++)
B[i] = mul(B[i - 1], base);
build(1, 1, n);
scanf("%lld", &q);
while(q--){
int opt, x, y, l, r;
scanf("%lld", &opt);
if(opt == 1){
scanf("%lld%lld", &x, &y);
modify(1, 1, n, x, y);
} else {
scanf("%lld%lld", &l, &r);
cnt = 0;
query(1, 1, n, l, r);
bool flg = false;
for(int i = 1; i <= cnt; i++){
if(t[sta[i]].flag){
flg = true;
break;
}
if(ans[i - 1].l.len < t[sta[i]].r.len){
flg = true;
break;
}
if(getval3(i - 1, t[sta[i]].r.len).val == t[sta[i]].r.val){
ans[i].r = Hash();
ans[i].l = ans[i - 1].l - t[sta[i]].r + t[sta[i]].l;
} else {
flg = true;
break;
}
}
if(ans[cnt].l.len || ans[cnt].r.len || flg)
printf("No\n");
else
printf("Yes\n");
}
}
return 0;
}
本文来自博客园,作者:Orange_new,转载请注明原文链接:https://www.cnblogs.com/JPGOJCZX/p/18752973


 浙公网安备 33010602011771号
浙公网安备 33010602011771号