可持久化数据结构学习笔记

可持久化基本概念

我们生活中经常会遇到这样的场景（也可能是出题人故意刁钻你），那就是我么需要访问一个历史版本的数据状态（比如 Ctrl z、开机还原、自动保存等），此时如果两个连续的历史版本之间差距比较小，且历史版本之间的差距比较好存储，那么我们可以考虑可持久化。

我们现在来打个比方，以此来解释可持久化的思路。

我们都喜欢刷短视频。短视频的每一秒都由特别多帧图片连续播放而成，可想而知，两帧图画之间的差距是非常小的。由于直接将每帧图画都完整存下来要花费大量空间，因此一般计算机只会存储每帧图画与前一帧不同的地方，我们播放视频的时候，只用不断将每一帧图画与上一帧不同的地方叠加在画面上即可。

如果我们将两帧图画做减法，那么我们可以得到一段时间内图画变化的信息。

可持久化线段树

类比视频的存储，我们可以建立多棵线段树，每一棵线段树就像一帧图画。相邻两棵线段树之间的差距非常小，因此每棵线段树只需要存储与前一棵的不同之处，相同的地方直接用前一颗线段树存储的信息即可。当我们将两棵线段树相减，就可以得到一段时间、区间或数位的线段树，而这棵线段树往往包含着题目的解。

说句闲话，可持久化线段树还有一个别称，叫做主席树。这个没有理论上的含义，主要因为在中国最早使用可持久化线段树的 Oier 叫做黄嘉泰（HJT）。

算法流程

我们拿主席树最经典的应用：“静态区间第 \(k\) 小值”来讲解可持久化线段树具体的算法流程。

洛谷 P3834 【模板】可持久化线段树 2

如果查找的是全局第 \(k\) 小，那么可以用权值线段树。但是现在是在区间上，如果我们给每一个区间都开一棵权值线段树，空间复杂度 \(\mathcal O(n^3)\)，直接爆炸。考虑一个简单的优化，我们只需要对每一个前缀开一棵线段树，一个区间的线段树，只用将两个前缀的线段树相减即可，但是这样空间复杂度依然是 \(\mathcal O(n^2)\) 的，依然无法通过。

考虑两个相邻前缀的线段树，我们发现后一棵线段树相较于前一棵线段树，只是多插入了一个数字，如果动态开点的话，最多只会新建 \(\mathcal O(\log n)\) 个节点。于是我们考虑能否只新建这些节点，其他节点直接用前一棵线段树的。

具体地，假设离散化后，整个序列为 \(2, 1, 3, 4\)，我们将这 \(4\) 棵前缀线段树画出来：

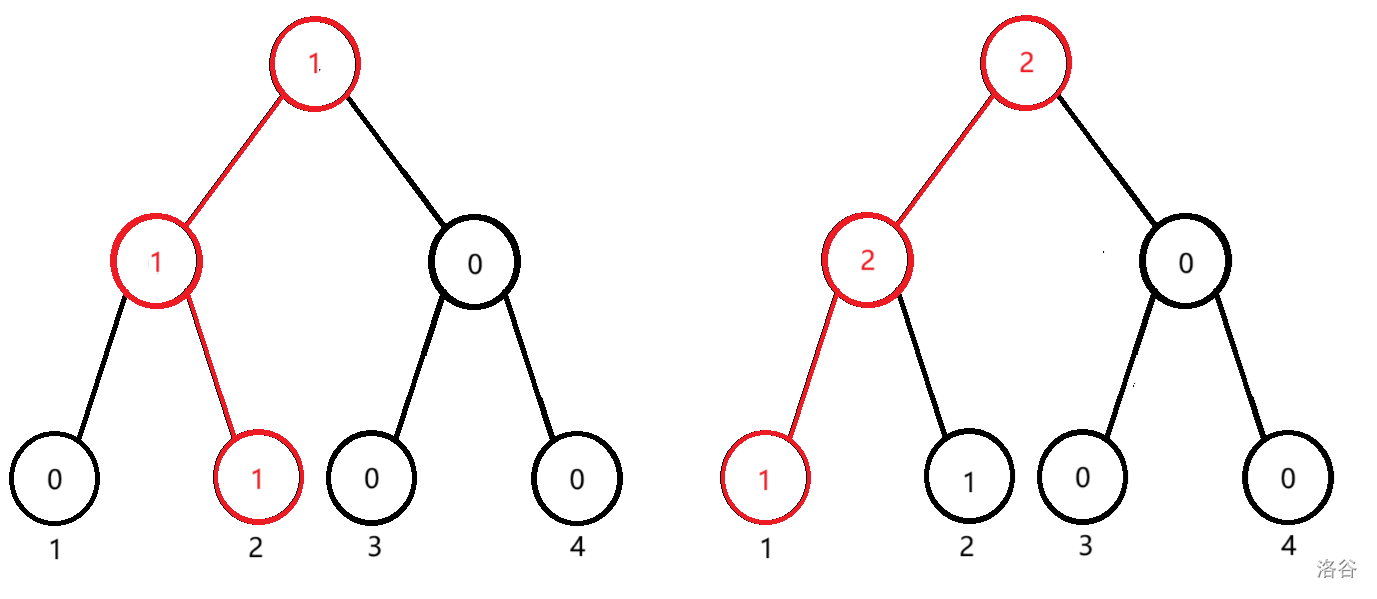
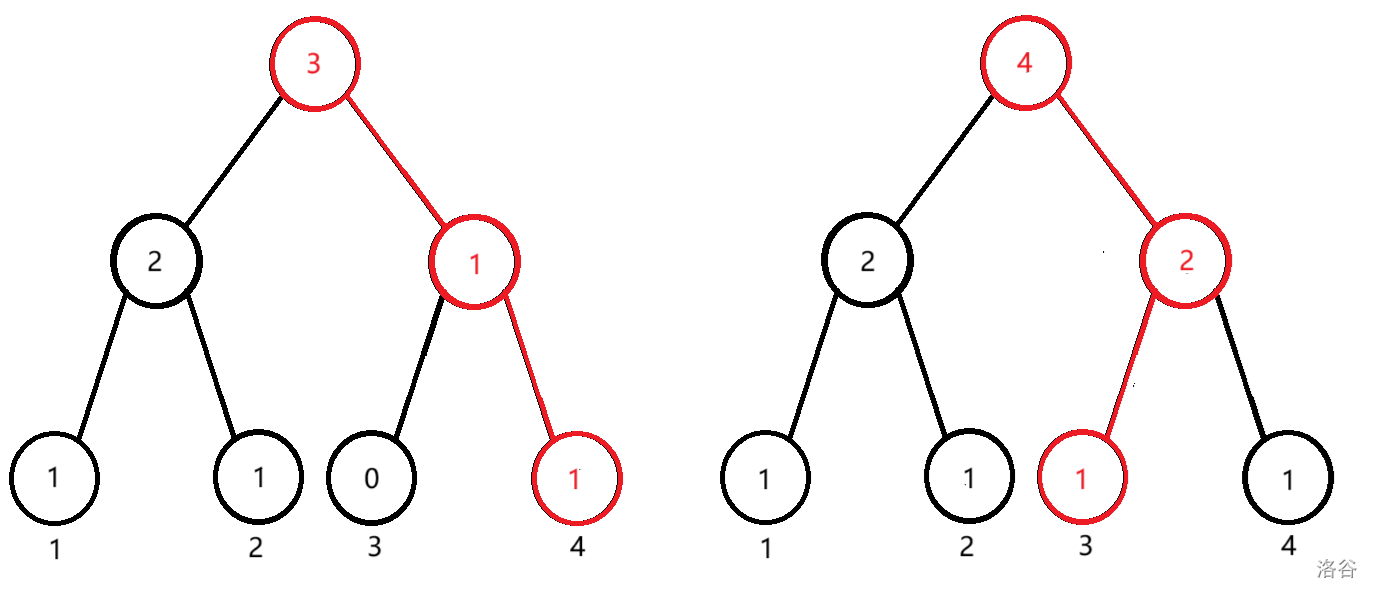
每次修改的树链被标红了。

我们新建一个空树，然后每次只把红色的链加入进来，对于一个新建的节点，如果它的某个儿子没有修改，那么直接连一条边到上一个版本对应的儿子上去。如图所示：

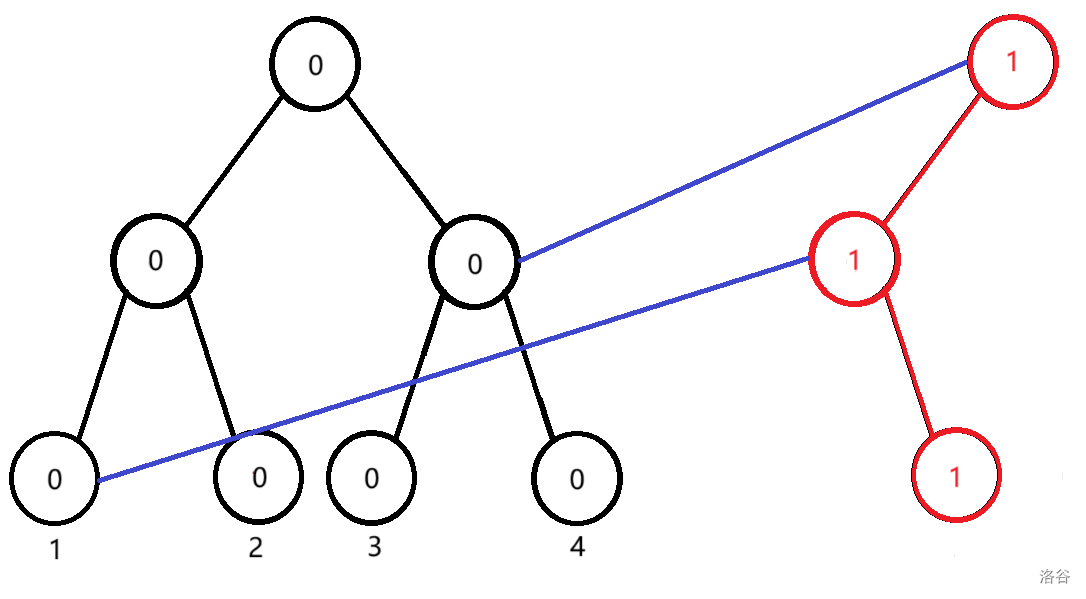
其实，一般情况下并不需要建出一棵空树来。因为空树的所有节点权值都为 \(0\)，任何一棵前缀线段树减它都不会发生变化，因此可以不建出这棵空树。

查询的时候，我们将两个前缀线段树差分，得到区间的线段树，然后直接在线段树上二分即可。

复杂度分析

由于每个前缀线段树只新建了 \(\mathcal O(\log n)\) 个节点，因此空间复杂度为 \(\mathcal O(n \log n)\)。

插入的时间复杂度显然是 \(O(\log n)\) 的，考虑查询，感觉将两颗线段数相减是 \(\mathcal O(n)\) 的，但是其实我们只需要将二分到的节点所存储的数字个数算出来即可，由于每次二分至少都缩小 \(\displaystyle\frac 12\)，因此这部分的时间复杂度是 \(\mathcal O(\log n)\) 的。因此最终的复杂度为 \(\mathcal O(n \log n) + \mathcal O(m \log n)\)

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 9;
int a[N], b[N], root[N], cnt, n, m;
struct{
	int L, R, sum;
} tree[N << 5];
int build(int pl, int pr){
	int rt = ++cnt;
	tree[rt].sum = 0;
	int mid = (pl + pr) >> 1;
	if(pl < pr){
		tree[rt].L = build(pl, mid);
		tree[rt].R = build(mid + 1, pr);
	}
	return rt;
}
int modify(int pre, int pl, int pr, int x){
	int rt = ++cnt;
	tree[rt].L = tree[pre].L;
	tree[rt].R = tree[pre].R;
	tree[rt].sum = tree[pre].sum + 1;
	int mid = (pl + pr) >> 1;
	if(pl < pr){
		if(x <= mid)
			tree[rt].L = modify(tree[pre].L, pl, mid, x);
		else
			tree[rt].R = modify(tree[pre].R, mid + 1, pr, x);
	}
	return rt;
}
int query(int u, int v, int pl, int pr, int k){
	if(pl == pr)
		return pl;
	int x = tree[tree[v].L].sum - tree[tree[u].L].sum;
	int mid = (pl + pr) >> 1;
	if(x >= k)
		return query(tree[u].L, tree[v].L, pl, mid, k);
	else
		return query(tree[u].R, tree[v].R, mid + 1, pr, k - x);
}
int main(){
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++){
		scanf("%d", &a[i]);
		b[i] = a[i];
	}
	sort(b + 1, b + n + 1);
	int size = unique(b + 1, b + n + 1) - (b + 1);
	for(int i = 1; i <= n; i++){
		int x = lower_bound(b + 1, b + size + 1, a[i]) - b;
		root[i] = modify(root[i - 1], 1, size, x);
	}
	while(m--){
		int x, y, k;
		scanf("%d%d%d", &x, &y, &k);
		printf("%d\n", b[query(root[x - 1], root[y], 1, size, k)]);
	}
	return 0;
}

洛谷 P1972 [SDOI2009] HH的项链

可持久化数组

洛谷 P3919 【模板】可持久化线段树 1（可持久化数组）

可持久化平衡树

可持久化并查集

可持久化可并堆

可持久化线性基

可持久化字典树

参考资料

• 《算法竞赛》罗勇军、郭卫斌