DP 学习笔记（四）：与数学有关的 DP 优化

子集和DP (SOS DP)

有点像是只有 \(0\) 或 \(1\) 的数位 \(DP\)。

子集和 \(DP\) 一般用来求解某类特殊的高维前缀和问题，这类问题在每个维度上只有 \(0 / 1\)，且每个点有点权。

举个例子：给定一个含 \(2^n\) 个整数的集合 \(A\)，对于任意一个集合 \(S \subseteq A\)，我们需要求 \(S\) 中所有元素的 \(A_i\) 和，即 \(F_i = \displaystyle\sum_{i \in S} A_i\)。

考虑普通的状压 \(DP\) 或枚举子集的想法，复杂度分别为 \(O(4^n)\) 或 \(O(3^n)\)，都太高了。其实，可以发现如果一个状态的二进制位上有 \(k\) 个 \(0\)，那么这个状态将会被遍历到 \(2^k - 1\) 次，考虑能否用 DP 的方法优化。

这次我们一位一位地 DP，记 \(F(S, i)\) 表示考虑 \(S\) 的所有子集，其中前 \(i\) 位与 \(S\) 一样，后面每位上可以与 \(S\) 不同的子集构成的集合，比如 \(F(1011010, 3) = \{1011010, 1011000, 1010010, 1010000\}\)，现在，如果 \(S\) 的第 \(i\) 位是 \(0\)，那么它的子集的第 \(i\) 位一定是 \(0\)，于是 \(F(S, i) = F(S, i - 1)\)。

如果 \(S\) 第 \(i\) 位上是 \(1\)，那么它的子集这一位上可能是 \(1\)，也可能是 \(0\)，如果子集这一位上是 \(1\)，那么 \(F(S, i)\) 依然 \(= F(S, i - 1)\)，如果这一位上是 \(0\)，那么它可以简化为 \(S \operatorname{xor} 2^i\) 的第一类的子集，于是 \(F(S, i) = F(S \operatorname{xor} 2^i, i - 1)\)，那么 \(DP\) 的顺序就被定了下来：

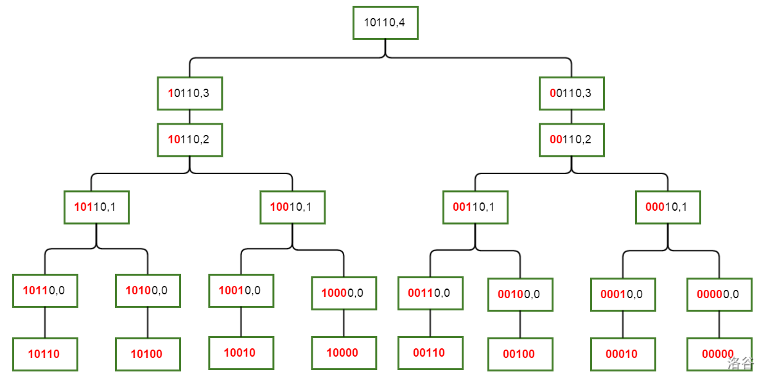
于是，设 \(f_{i, j}\) 表示当前集合为 \(j\)，前 \(i\) 位必须与 \(j\) 相同的子集的权值和，于是 DP 方程可以写成 \(f_{i, j} = \begin{cases} f_{i - 1, j} & j 的第 i 位为 0 \\ f_{i - 1, j} + f_{i - 1, j \operatorname{xor} 2^i} & j 的第 i 位为 1\end{cases}\)。

可以发现 \(f_{i}\) 只与 \(f_{i - 1}\) 有关，于是可以滚动数组优化，考虑到 \(j \operatorname{xor} 2^i < j\)，于是内层循环需要倒序枚举。

完整代码：其实很短

for(int i = 0; i < (1 << n); i++)
    f[i] = a[i];
for(int j = 0; j < n; j++)
    for(int i = 0; i < (1 << n); i++)
        if(((i >> j) & 1) == 0)
            f[i | (1 << j)] += f[i];

复杂度为 \(O(n 2^n)\)。

例题一

例题二

动态DP

狭义矩阵乘法

先从最基础的 DP，也就是递推讲起。

首先，递推分为线性递推和非线性递推，非线性递推比如 Somos-4 序列（\(1, 1, 1, 1, 2, 3, 7, 23, 59, \dots\)），它的递推式是 \(f_i = \begin{cases} 1 & i \in \{0, 1, 2, 3\} \\ \displaystyle\frac{f_{n - 1} f_{n - 3} + f_{n - 2}^2}{f_{n - 4}} & i \geq 4\end{cases}\)，其中出现了 \(2\) 次项与 \(-1\) 次项，因此不是线性的，在这里不做讨论。

常见的线性 DP 又分为以下 \(3\) 种：

• 常系数线性递推。通常可以写成：\(f_n = \displaystyle\sum_{i = 1}^k c_i f_{n - i}\)，其中 \(c_i\) 是常数。比如几何级数：\(1, q, q^2, q^3, \dots\)，或者斐波那契数列：\(f_i = \begin{cases} 1 & i \in \{1, 2\} \\ f_{i - 1} + f_{i - 2} & i \geq 3 \end{cases}\)；

• 普通整式递推。通常可以写成：\(f_n = \displaystyle\sum_{i = 1}^k c_i(n) f_{n - i}\)，其中 \(c_i(n)\) 是关于 \(n\) 的函数。比如阶乘序列：\(1, 2, 6, 24, \dots\)，或者莫茨金序列：\(f_i = \begin{cases} 1 & i \in\{0, 1\} \\ \displaystyle\frac{2n + 1}{n + 2}f_{i - 1} + \frac{3n - 3}{n + 2}f_{i - 2} & i \geq 2\end{cases}\)；

• 含 \(q, q^n\) 双参的整式递推。通常可以写成：：\(f_n = \displaystyle\sum_{i = 1}^k c_i(q, q^n) f_{n - i}\)，其中 \(c_i(q, q^n)\) 是关于 \(q\) 和 \(q_n\) 的函数。比如 \(q\) 阶乘序列：\([n]_q! = (1 + q) \dots (1 + q + \dots + q^{n - 1})\)。

在这里，我们只解决常系数线性递推，而常系数线性递推又分为常系数齐次线性递推和常系数非齐次线性地推。动态 DP 一般解决常系数齐次线性递推问题在小数据范围内的求解（可见这只是冰上一角，但这一角也能把你压垮）。

考虑到 \(f_i\) 的值只与 \(f_{i - 1}\) 到 \(f_{i - k}\) 相关，那么我们可以考虑将 \(f_{i - 1}\) 到 \(f_{i - k}\) 从上到下排列形成一个向量 \(\begin{bmatrix} f_{i - 1} \\ f_{i - 2} \\ \vdots \\ f_{i - k}\end{bmatrix}\)，这时，如果找到一个矩阵 \(A\)，使得 \(A \begin{bmatrix} f_{i - 1} \\ f_{i - 2} \\ \vdots \\ f_{i - k}\end{bmatrix} = \begin{bmatrix} f_i \\ f_{i - 1} \\ \vdots \\ f_{i - k + 1}\end{bmatrix}\)，那么我们就可以通过不断乘以 \(A\) 的形式来表示递推。事实上，这个矩阵 \(A\) 就是\(\begin{bmatrix} c_1 & c_2 & c_3 & \dots & c_{k - 1} & c_k \\ 1 & 0 & 0 & \dots & 0 & 0 \\ 0 & 1 & 0 & \dots & 0 & 0 \\ 0 & 0 & 1 & \dots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \dots & 1 & 0\\ \end{bmatrix}\)，现在，我们就可以用快速幂优化不断乘以 \(A\) 的操作，做到 \(O(\log_2 nk^3)\)（\(k\) 为矩阵边长）。

广义矩阵乘法

拉格朗日插值优化 DP

生成函数（FFT）优化 DP

参考资料

• 黄kx 的课件

• SOS DP 学习笔记 cyl06

• [dp 小计] SOSdp g1ove