字符串学习笔记（二）：自动机

自动机

Trie

AC 自动机（\(\text{ACAM}\)）

回文自动机（\(\text{PAM}\)）

后缀数组（\(\text{SA}\)）

后缀自动机（\(\text{SAM}\)）

这是一个超级厉害的字符串算法，我觉得它仅次于字符串哈希，基本可以解决一切子串相关问题。

和 ACAM、PAM 不同，后缀自动机是一个 DAG，从根节点走到任意一个点的路径都是原串的一个子串。因此，可以有一个最暴力的思路，就是把所有子串全部插入一个 Trie 中，但这样时空复杂度都爆了。考虑到一个子串一定是某个后缀的前缀，因此我们可以把所有后缀插入 Trie 中（这也是后缀自动机的名字由来），但这样时空复杂度依然是 \(O(n^2)\) 的，考虑进一步优化。其实有一个比较显然的想法，如果两个后缀有最长公共后缀，我们其实可以把它们合在一起，此时这个 Trie 树就变成了一个 DAG。

比如 \(\text{ababaa}\) 的 SAM 长这个样子：

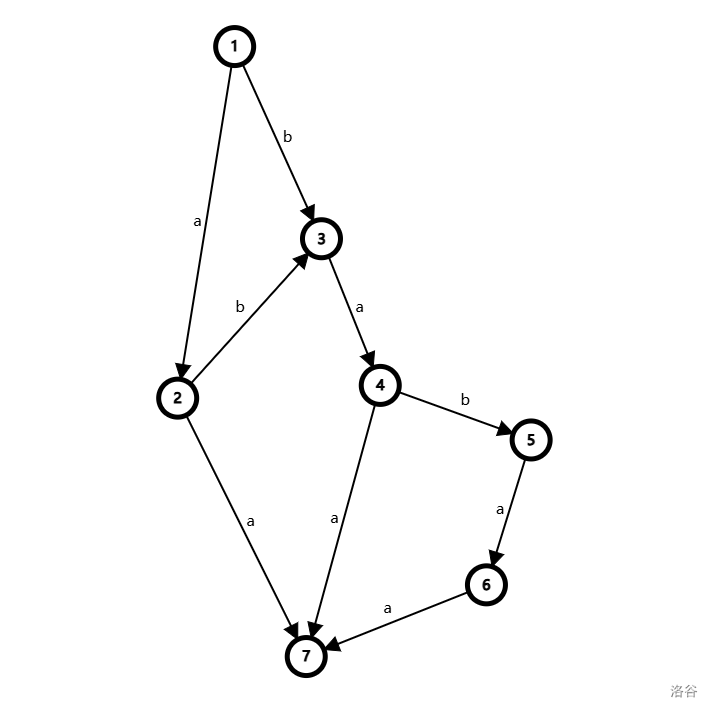
下面来详细介绍如何构造。

\(\operatorname{endpos}\)

设字符串 \(s\) 的一个非空子串 \(s'\) 在 \(s\) 中所有结尾的位置构成的集合为 \(\operatorname{endpos}\)。举个例子，对于字符串 \(S = ababaa\)，\(\operatorname{endpos}(a) = \{1, 3, 5, 6\}, \operatorname{endpos}(ab) = \{1, 3\}\)。

显然，两个子串的 \(\operatorname{endpos}\) 可能相同，因此我们可以根据 \(\operatorname{endpos}\) 将 \(S\)，的子串划分为若干个集合，每个集合中所有子串的 \(\operatorname{endpos}\) 相同，此时我们就定义划分出来的这几个集合叫做 \(\operatorname{endpos}\) 等价类。

\(\operatorname{endpos}\) 有一些优美的性质，在后续构建 SAM 时很有用处：

• 对于字符串的任意非空子串 \(u\) 与 \(v\)，如果 \(\operatorname{endpos}(u) = \operatorname{endpos}(v)\)，且 \(|u| \leq |v|\)，那么 \(u\) 是 \(v\) 的后缀。

  证：这个应该很好理解，如果 \(u\) 和 \(v\) 所有结束位置都一样，\(u\) 的长度还比 \(v\) 段大，说明 \(v\) 是在 \(u\) 前面增加了几个字符，因此 \(u\) 是 \(v\) 的后缀。

• 对于字符串的任意非空子串 \(u\) 与 \(v\)，如果 \(|u| \leq |v|\)，那么 \(\operatorname{endpos}(v) \in \operatorname{endpos}(u)\) 或者 \(\operatorname{endpos}(u) \cap \operatorname{endpos}(v) = \emptyset\)。

  证：如果 \(u\) 是 \(v\) 的子串，那么 \(v\) 出现时 \(u\) 一定出现，于是 \(\operatorname{endpos}(v) \in \operatorname{endpos}(u)\)，否则 \(u\) 与 \(v\) 一定不会同时出现。

• 对于任意一个 \(\operatorname{endpos}\) 等价类，其中的所有子串将它们按长度从大到小排序，那么每一个子串都是前一个子串的后缀，长度 \(=\) 前者 \(−1\)。

  证：如果等价类仅包含一个字符串那么这条性质显然成立，否则设 \(u\) 为该等价类最短的字符串，\(v\) 为最长的字符串，那么 \(v\) 的所有长度 \(\leq |u|\) 的后缀，根据性质 \(2\)，它们也一定属于这一等价类中。

后缀链接（\(\text{parent}\) 树）

可以发现，我们设 \(v\) 为该等价类最长的子串，在 \(v\) 前加另一个字符，得到一个新的字符串 \(u\)，如果 \(u\) 依然是原串的子串，那么 \(\operatorname{endpos}(u) \neq \operatorname{endpos}(v)\)，且 \(\operatorname{endpos}(u) \in \operatorname{endpos}(v)\)，此时，我们就可以把 \(\operatorname{endpos}(v)\) 作为 \(\operatorname{endpos}(u)\) 的父亲，构成一棵树的形态，此时这棵树就叫做 \(\text{parent}\) 树。

可以发现，在 SAM 上走边是在字符串后面添加字符，而在\(\text{parent}\) 树上跳儿子也是在字符串后面加字符，可以感性理解一下，每个 \(\text{parent}\) 上的节点正好也是 SAM 上的一个点。我们希望能在 \(\text{parent}\) 树的节点之间连边，使从起点出发到任意点的路径都对应属于该点的一个字符串，此时就可以构造出 SAM 了。

比如 \(\text{ababaa}\) 的 \(\text{parent}\) 树，我们设根节点为空串，它对应的 \(\operatorname{endpos}\) 集合为全集，那么这棵树就长这个样子：

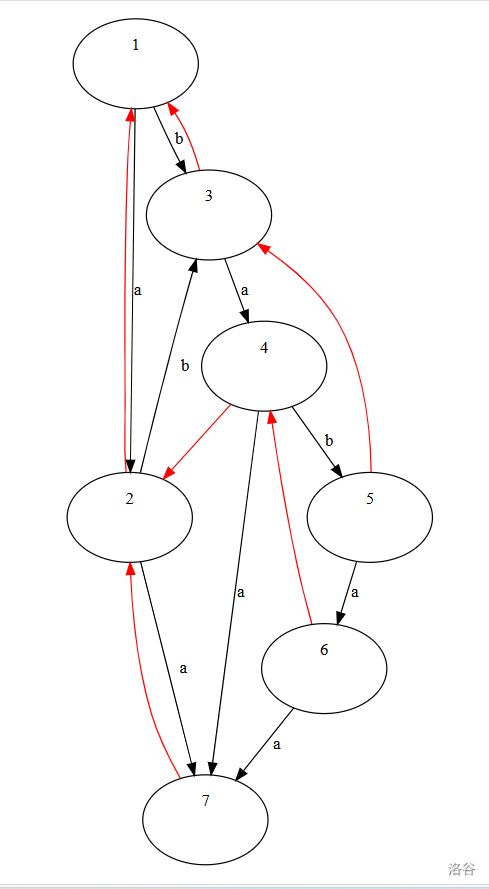
（其中黑色边为 \(\text{SAM}\) 上的边，红色的边为 \(\text{parent}\) 树上的边）

\(\text{SAM}\) 的构造

现在考虑如何在线性复杂度内构造 SAM，我们将所有字符依次加入 SAM 中。在加入第 \(i\) 个字符时，已经维护好了 \([1, i - 1]\) 这个串构成的 SAM。

我们规定，\(fa_i\) 表示第 \(i\) 个点在 \(\text{parent}\) 树上的父亲，\(len_i\) 表示从起点出发到 \(i\) 点的所有路径对应的字符串中长度的最大值，\(ch_{i, [1, 26]}\) 表示 \(i\) 的所有出边。

首先，新加入的这个字符 \(c\) 所产生的长度为 \(i\) 的字符串是之前从未有过的，因此，我们一定会在前 \(i - 1\) 个字符构成的字符串所对应路径的后面加上 \(c\)：

int p = lst, nw = lst = ++tot;
t[nw].len = t[p].len + 1;

现在我们需要修改一些节点的 \(ch\) 信息。考虑哪些串的 \(ch\) 会被修改，那一定是原先 \(i - 1\) 个字符所对应的串的一个后缀。由于在 \(\text{parent}\) 树上跳父亲就是在当前字符串前面删字符，正好可以遍历到所有后缀，于是我们直接在 \(\text{parent}\) 树上跳父亲，把遍历到的节点的 \(ch\) 信息修改一下就可以了：

for(; p && !t[p].ch[c]; p = t[p].fa)
  t[p].ch[c] = nw;

如果直接跳到根了，那么证明原先 \(i - 1\) 个字符中没有 \(c\)，那么直接把当前节点在 \(\text{parent}\) 树上的父亲赋值为根节点即可：

if(!p){
  t[nw].fa = 1;
  return;
}

否则一定有一个点 \(p\)，它存在一个儿子 \(q\)，它们之间的边是字符 \(c\)。

时间复杂度

空间复杂度

最小化证明

\(\text{SAM}\) 的应用

后缀树

广义后缀自动机（广义 \(\text{SAM}\)）

子序列自动机

自动机 DP