图上算法学习笔记（三）：二分图、网络流
二分图
定义
如果你能把一个图划分成两个集合，集合内部的点没有边相连接，那么这个图就是一个二分图，如图就是一个二分图：
交错路：从一个没有被匹配的点出发，依次走非匹配边，匹配边，非匹配边 …… 最后到达另外一部点当中某个没有被匹配的点的路径。
增广路：从一个没有被匹配的点出发，依次走非匹配边，匹配边，非匹配边 …… 最后通过一条非匹配边到达另外一部点当中某个没有被匹配的点的路径。
性质
一个图是二分图当且仅当它不存在长度为奇数的环。
证：在二分图中，每走一条边就会切换一次集合，只有走偶数条边才可以回到原来的集合，才有可能回到原来的点，因此二分图中的环都是偶数长度的。
反过来，如果一个图只存在长度为偶数的环，那么可以对这张图黑白染色，使得一条边上的两个点颜色不同，那么将染成黑色的点分为一个集合，染成白色的点分为一个集合，就可以得到一个二分图。
这个性质可以在 \(O(|V| + |E|)\) 的复杂度内判断一个图是否是二分图。
二分图的匹配
二分图的一个匹配指的是一个边集的子集 \(E' \subseteq E\) 且 \(E'\) 中任意两条边都不存在公共顶点 (就像一个男人不会拥有两个老婆)
二分图最大匹配
对于一个二分图，他的最大匹配就是它所有匹配中边数的最大值。
匈牙利算法
匈牙利算法可以在 \(O(|V||E|)\) 的时间复杂度内求出一个二分图的最大匹配。
匈牙利算法每次枚举一个点 \(u\)，遍历和这个点连接的所有边，尝试将这个边作为匹配边去更新答案，如果这条边的另一个节点 \(v\) 没有被匹配过，那么直接匹配；如果 \(v\) 已经被匹配过了，那么尝试更改 \(v\) 的匹配边，如果 \(v\) 的匹配边可以被更改，那么就将匹配边修改，再将 \(u, v\) 之间的边标记为匹配。
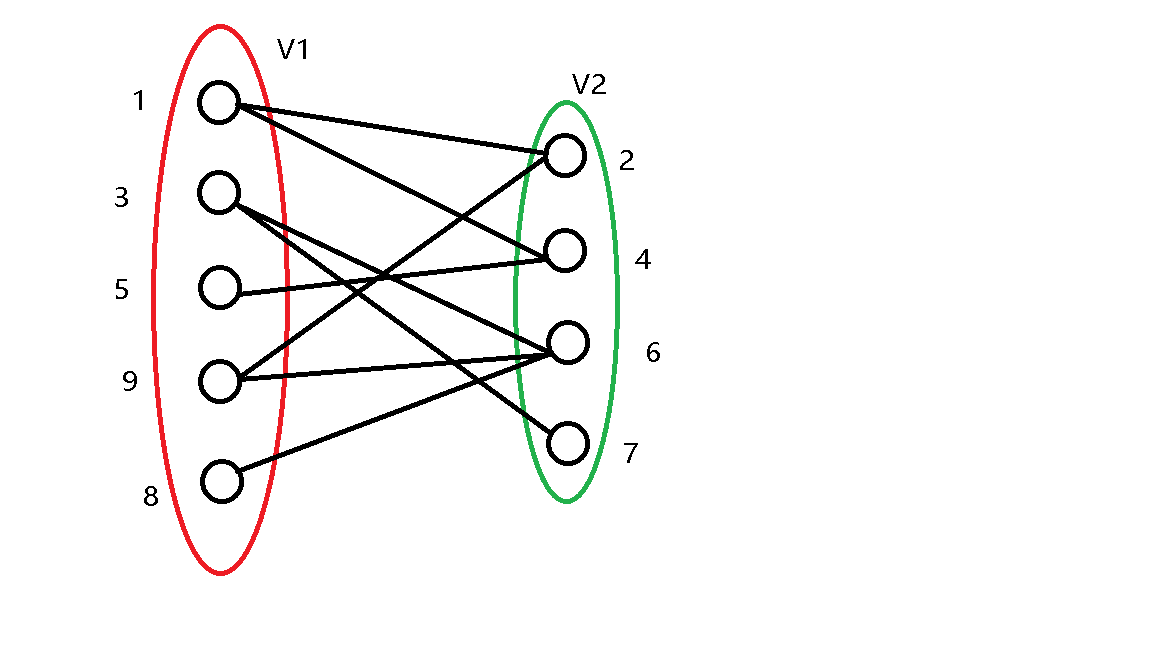
举个例子：对于二分图
从 \(1\) 号点开始，直接匹配。
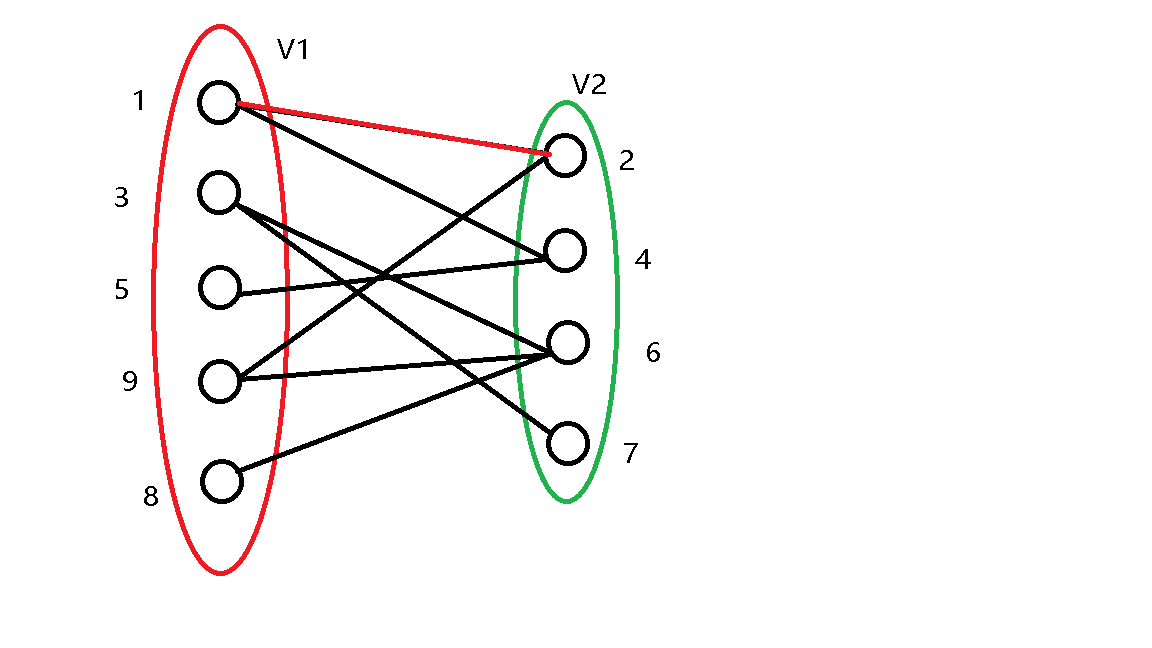
\(2\) 号点被标记过了，跳过。
\(3\) 号点也直接匹配。
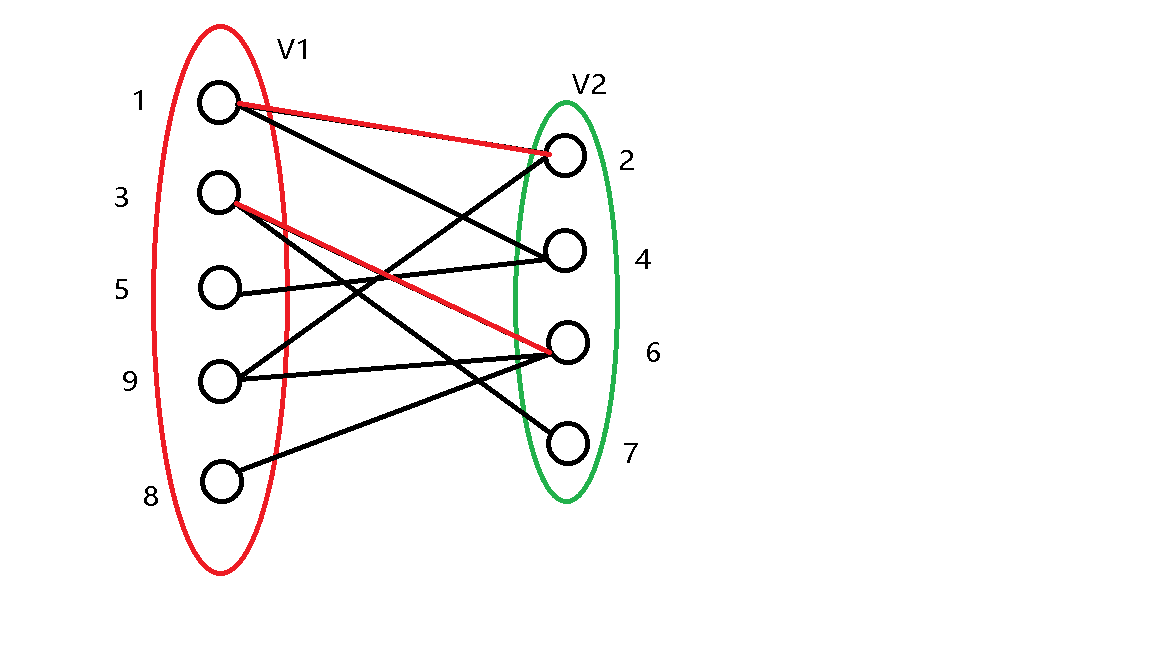
\(4\) 号点也直接匹配。
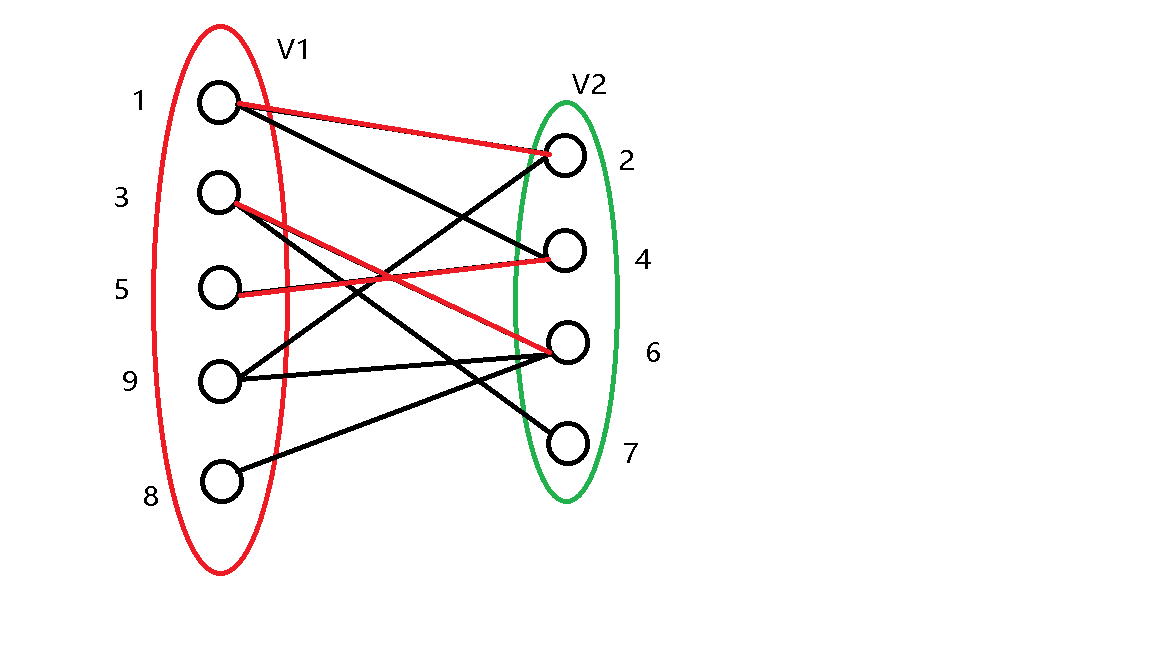
\(5\) 号点被匹配过了，跳过。
\(6\) 号点被匹配过了，跳过。
\(7\) 号点与 \(3\) 号点之间有边，尝试将这个边标记为匹配。
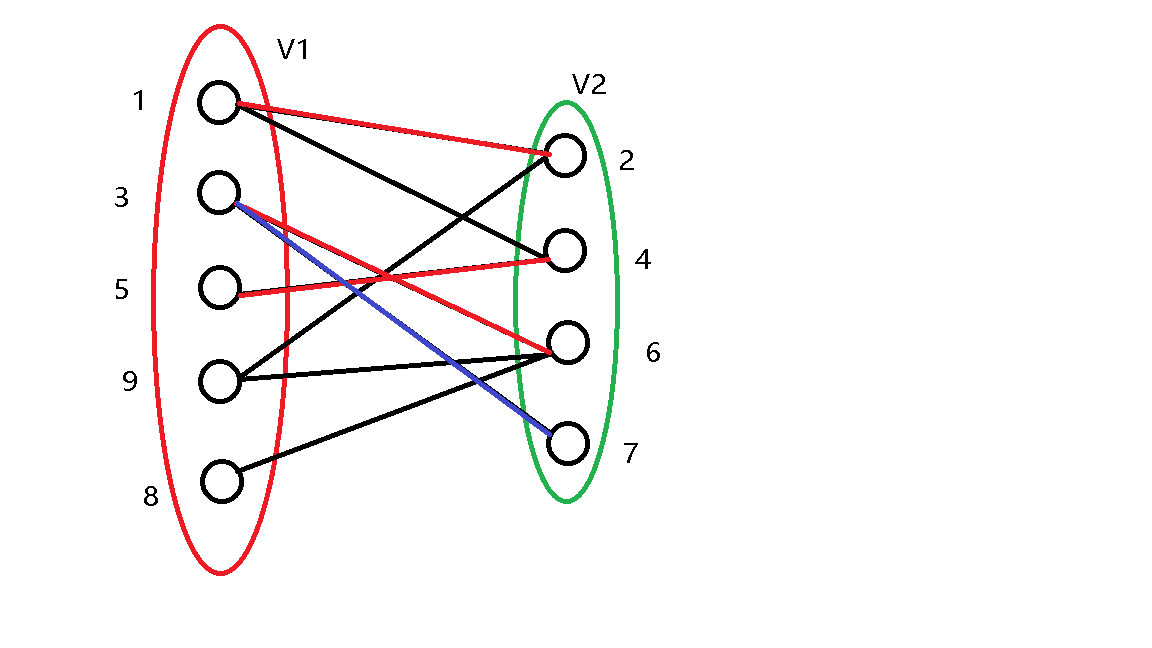
发现 \(3\) 号点已经被 \(6\) 号点匹配，继续尝试更改 \(6\) 号点的匹配，发现 \(6\) 号节点可以与 \(9\) 号点匹配，那么将 \(6\) 号和 \(9\) 号点匹配，\(3\) 号点与 \(7\) 号店匹配。
\(8\) 号点与 \(6\) 号点之间有边，尝试将这个边标记为匹配。
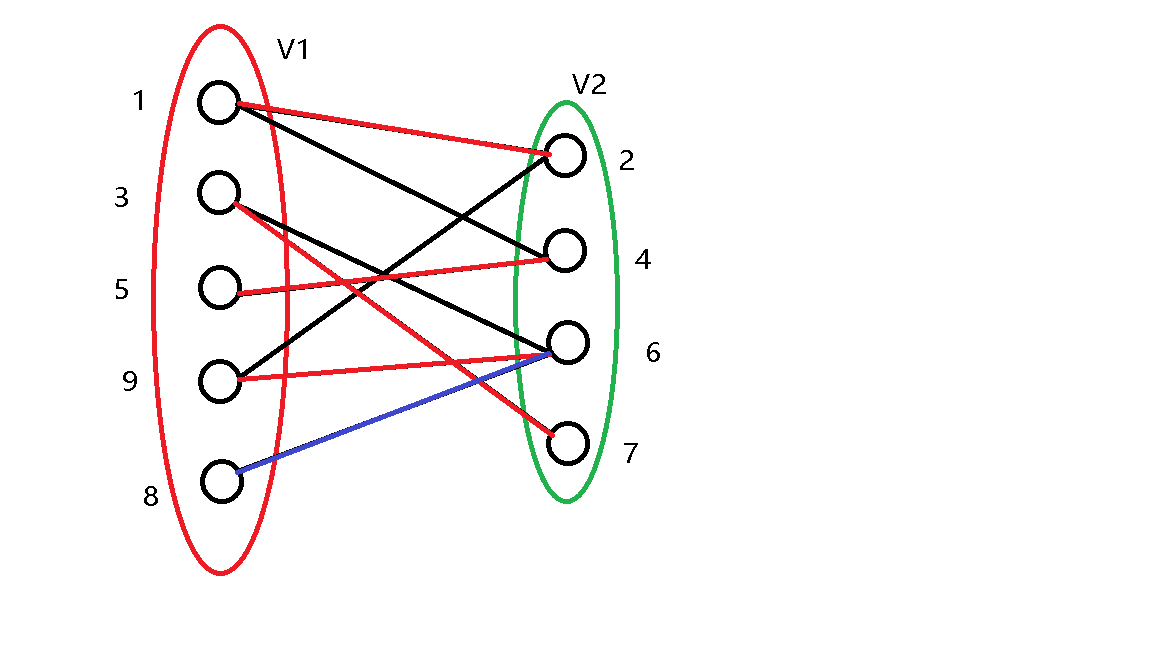
发现 \(6\) 号点已经被 \(9\) 号点匹配，继续尝试更改 \(9\) 号点的匹配。
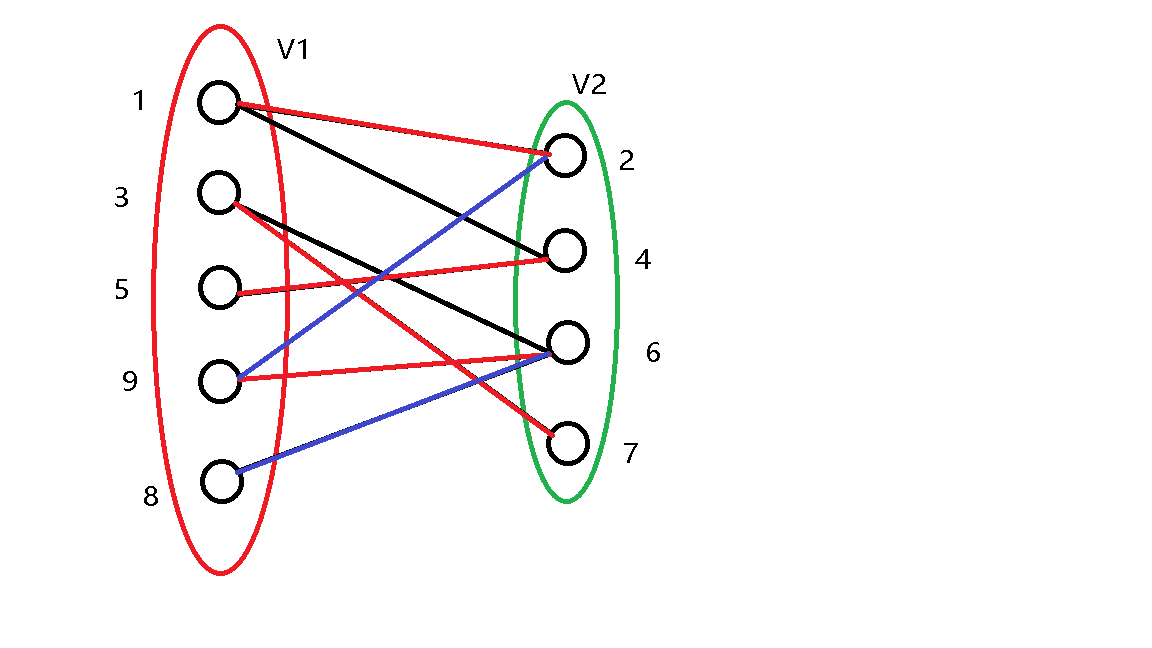
发现 \(2\) 号点已经被 \(1\) 号点匹配，继续尝试更改 \(1\) 号点的匹配。
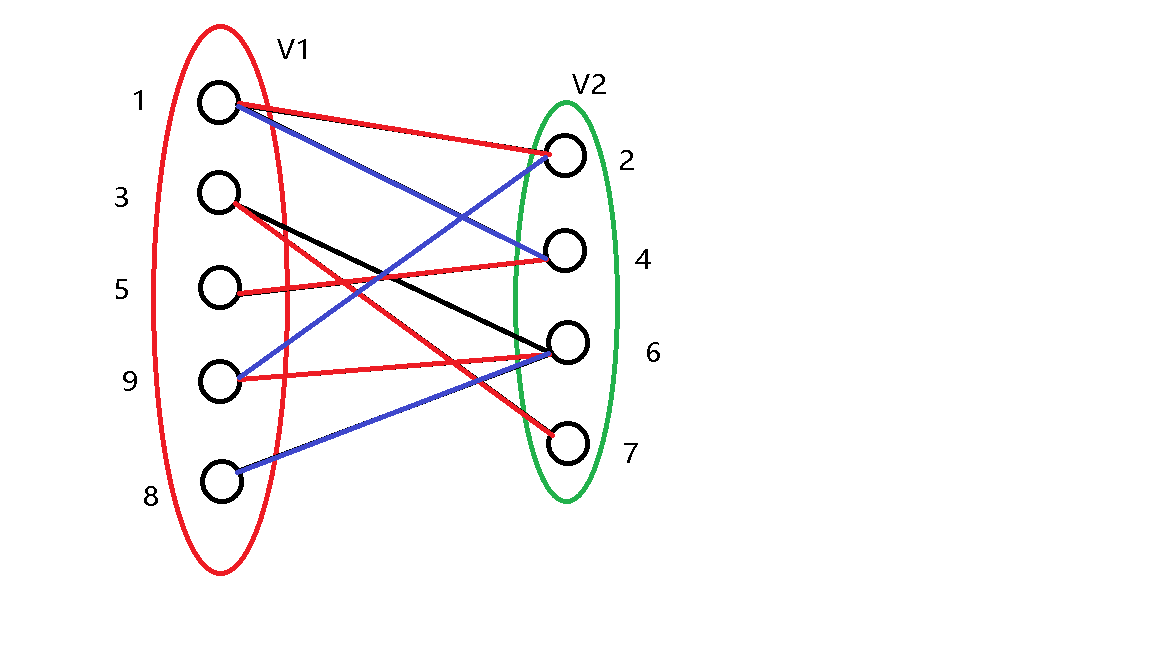
发现 \(4\) 号点已经被 \(5\) 号点匹配，继续尝试更改 \(5\) 号点的匹配，发现 \(5\) 号点无法更改匹配，说明本次尝试无法更改匹配。
\(9\) 号点被匹配过了，跳过。
这样就得出了最终匹配：
可以发现：此过程相当于对每个点寻找它的增广路，，然后切换所有边的匹配状态，以此增加匹配数。
完整代码：洛谷 P3386 【模板】二分图最大匹配
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int G[510][510];
int match[510], reserve_boy[510];//match[i]表示i号点的匹配对象（图上红边），reverse_boy[i]表示尝试匹配中i号点是否被匹配（图上蓝边）
int n, m;
bool dfs(int x){
for(int i = 1; i <= m; i++)
if(!reserve_boy[i] && G[x][i]){
reserve_boy[i] = 1;//这个点标记为被匹配
if(!match[i] || dfs(match[i])){//这个点没被匹配货可以更改匹配
match[i] = x;//更新匹配
return true;
}
}
return false;
}
int main(){
int e;
scanf("%d%d%d", &n, &m, &e);
while(e--){
int a, b;
scanf("%d%d", &a, &b);
G[a][b] = 1;
}
int sum = 0;
for(int i = 1; i <= n; i++){
memset(reserve_boy, 0, sizeof(reserve_boy));
if(dfs(i))
sum++;
}
printf("%d\n", sum);
return 0;
}
最大流算法
讲到最大流时会讲，此处不做阐述。
二分图完美匹配
对于一个二分图，如果它的两个点集点数相等且他的最大匹配数量等于任意一个点集大小，那么就称这是这个二分图的一个完美匹配。
二分图最大权完美匹配
KM 算法
匈牙利算法可以在 \(O(|V| ^ 4)\) 的时间复杂度内求出一个二分图的最大权完美匹配。
先来两个定义：
-
可行顶标：给每个点赋值一个点权 \(l_u\)，满足 \(\forall (u, v) \in E\)，\(w_{u, v} \leq l_u + l_v\)
-
相等子图：原图的一个生成子图，包括了原图所有的点，包含且仅包含满足 \(w_{u, v} = l_u + l_v\) 的边 \((u, v) \in E\)
定理1.3.1
对于某组可行顶标，如果根据这组可行顶标构造的相等子图存在完美匹配，那么，该匹配就是原二分图的最大权完美匹配。
证：考虑任意一组完美匹配 \(M\)，其边权和为：\(\displaystyle\sum_{(u, v) \in M}w_{u, v} \leq \sum_{(u, v) \in M} l(u) + l(v)\) (可行顶标的定义) \(= \displaystyle\sum_{u \in V} l(u)\) (二分图完美匹配的定义)
而这个相等子图的完美匹配的边权和为 \(\displaystyle\sum_{u \in V} l(u)\)，因此一定是最大权完美匹配。
于是现在问题变成了调整可行顶标，使得相等子图存在完美匹配。
初始时我们随便给所有顶点一个可行的可行顶标(一般设 \(l_u = \operatorname{max}_{1 \leq j \leq n}w_{i, j}, l_v = 0\))。然后每次选出左部点中第一个没有匹配的点，遍历所有从它出发的在相等子图中的交错路，如果存在增广路就将增广路上的所有边切换匹配状态。
否则记左部点中在交错路中的集合为 \(S_1\)，没在的为 \(S_2\)，右部点的为 \(T_1\) 和 \(T_2\)。
那么在相等子图中的边有如下的事实：
-
不存在 \(S_1 \rightarrow T_2\) 的边，否则从 \(S_1\) 中的点出发的交错路会到达 \(T_2\) 中的点。
-
如果存在 \(S_2 \rightarrow T_1\) 的边，那一定不是匹配边，否则这个 \(S_2\) 中的点应该属于 \(S_1\)
现在开始协调调已经有匹配的左部点的顶标，我们考虑给 \(S_1\) 的所有点的顶标减去一个数 a，给 \(T_1\) 的所有点的顶标加上 a。那么有：
-
\(S_1 \rightarrow T_1\) 的边不会变化，因为它们中的点在交错路上，满足 \(l_u + l_v = w_{u, v}\)
-
\(S_2 \rightarrow T_2\) 的边不会变化，因为它们的可行顶标没有发生变化。
-
\(S_1 \rightarrow T_2\) 的边可能加入相等子图，因为 \(l_u\) 减小，\(l_v\) 不变，\(l_u + l_v\) 减小。
-
\(S_2 \rightarrow T_1\) 的边不可能加入相等子图，因为 \(l_u\) 不变，\(l_v\) 增大，\(l_u + l_v\) 增大。
因此我们要让 \(S_1 \rightarrow T_2\) 中的最大的边恰好加入相等子图，即：\(a = \operatorname{min}_{u \in S_1, v \in S_2}{l_u + l_v - w_{u, v}}\)
对 \(T_1\) 中的每个点 \(v\) 维护 \(slack_v = \operatorname{min}_{u \in S_1}{l_u + l_v - w_{u, v}}\)，那么每次修改顶标后可以通过 \(a = \operatorname{min}_{v \in T_2}slack_v\) 更新 \(a\)
这个协调的过程最多进行 \(|V|\) 次就可以找到一条增广路。于是朴素维护的复杂度为 \(O(|V| ^ 4)\)
采用DFS，就是最朴素的写法。
举个例子：对于二分图
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e2 + 9, M = 3e5 + 9, inf = 0x3f3f3f3f3f3f3f3f;
int w[N][N], slack[N];
int lx[N], ly[N];
bool visx[N], visy[N];
int matx[N], maty[N], pre[N], n, m;
queue <int> q;
bool check(int x){
visy[x] = 1;
if(maty[x]){
q.push(maty[x]);
return false;
}
while(x){
maty[x] = pre[x];
int t = matx[pre[x]];
matx[pre[x]] = x;
x = t;
}
return true;
}
bool bfs(){
while(!q.empty()){
int u = q.front();
q.pop();
if(visx[u])
continue;
visx[u] = 1;
for(int v = 1; v <= n; v++){
if(w[u][v] != -inf){
if(visy[v])
continue;
if(lx[u] + ly[v] - w[u][v] < slack[v]){
slack[v] = lx[u] + ly[v] - w[u][v];
pre[v] = u;
if(!slack[v] && check(v))
return true;
}
}
}
}
int delta = inf;
for(int i = 1; i <= n; i++)
if(!visy[i])
delta = min(delta, slack[i]);
for(int i = 1; i <= n; i++){
if(visx[i])
lx[i] -= delta;
if(visy[i])
ly[i] += delta;
else
slack[i] -= delta;
}
for(int i = 1; i <= n; i++)
if(!visy[i] && !slack[i] && check(i))
return true;
return false;
}
int KM(){
for(int i = 1; i <= n; i++){
lx[i] = -inf;
for(int j = 1; j <= n; j++)
lx[i] = max(lx[i], w[i][j]);
}
for(int i = 1; i <= n; i++){
memset(slack, 0x3f, sizeof(slack));
memset(visx, 0, sizeof(visx));
memset(visy, 0, sizeof(visy));
while(!q.empty())
q.pop();
q.push(i);
while(!bfs());
}
int ret = 0;
for(int i = 1; i <= n; i++)
ret += w[maty[i]][i];
return ret;
}
signed main(){
scanf("%lld%lld", &n, &m);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
w[i][j] = -inf;
for(int i = 1; i <= m; i++){
int u, v, x;
scanf("%lld%lld%lld",&u, &v, &x);
w[u][v] = max(w[u][v], x);
}
printf("%lld\n", KM());
for(int i = 1; i <= n; i++)
printf("%lld ", maty[i]);
return 0;
}
费用流算法
讲到费用流时会讲，此处不做阐述。
二分图的应用：最小点覆盖
定义：对于一张二分图，它的点覆盖是一个点集的子集，满足每条边都恰好有一个顶点在这个子集中。
它的最小点覆盖则是所有点覆盖中集合大小最小的点覆盖。
定理1.4.1
对于一张二分图，其最大匹配数等于其最小点覆盖数。
证：考虑如果存在完美匹配则显然。否则设已经有了一个匹配且右部点没有全部匹配，
然后从右边的每个非匹配点出发找增广路，把经过的所有节点标注出来，如图：
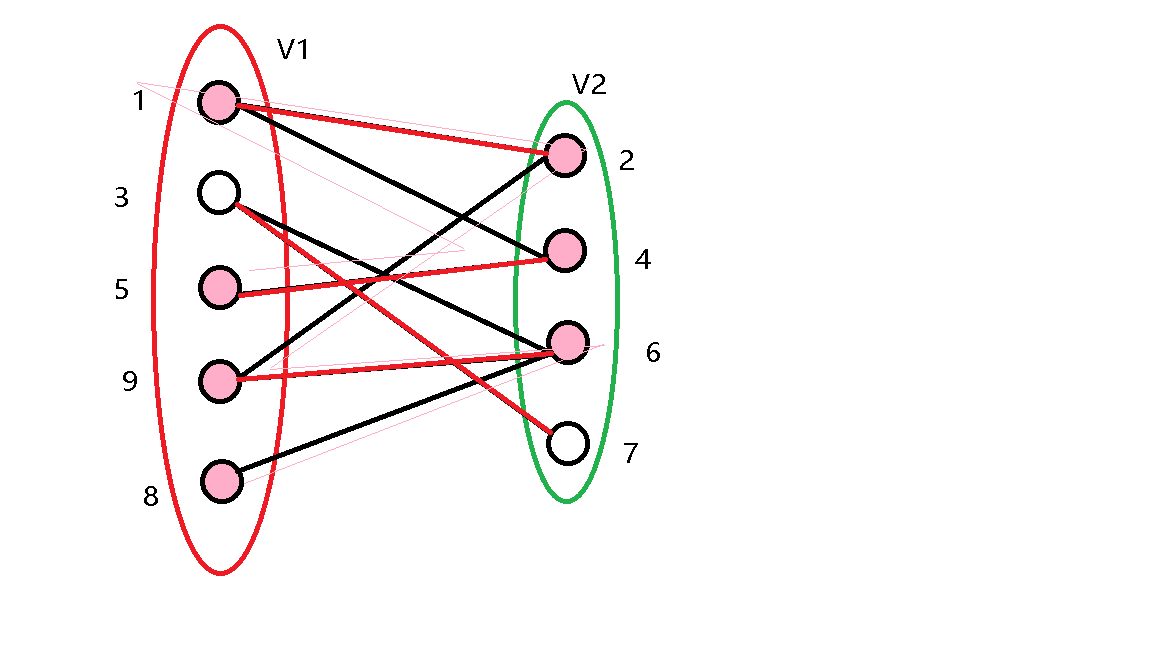(粉色细线为增广路)
这时候我们把右部点中没有被标记的点拿出来，左部点被标记的点拿出来。
分别考虑左部点和右部点。对于左部点：如果它不是匹配点，那么找到了一条增广路，匹配可以增大；对于右部点：如果它不是匹配点，那么一定会从它出发寻找非匹配边。
\(\therefore\) . 所有拿出来的点都是匹配点。
再次是分别考虑左部点和右部点。考虑右边的标记点连出来的边，假设它左边的点没有标记(那么该右部点一定是匹配点)，那么有两种情况：
-
该点不是匹配点：那么这条边一定不是匹配边，于是可以加入交错路，左部点不可能不标记.
-
该点是匹配点：那么这条边一定是匹配边，但是这样右部点就不可能被标记
左部点的情况同理。
\(\therefore\) 拿出来的点构成一个点覆盖。
覆盖所有匹配边就至少需要这么多点。
至此，我们证明了最大匹配等于最小覆盖，并给出了一种可行的构造方案。
二分图的应用：最大独立集
定义：对于一张二分图，那些没有边直接的顶点组成的集合。
它的最大独立集则是所有独立集中集合大小最大的独立集。
定理1.5.1
对于一张二分图，其最大点独立集数 \(U\) 等于其总点数减去最大匹配数 \(M\) 。
证：考虑把最小点覆盖的点全部去掉一定构成一个独立集，也即 \(U \geq n − M\)
另一方面，所有匹配里面最多选择一个点，也即 \(U \leq n − M\)，于是有 \(U = n − M\)
网络流
网络的基本概念
网络是指一种特殊的有向图 \(G = (V, E)\)，其与一般有向图的不同之处在于有容量和源汇点。
\(E\) 中每条边 \((u, v)\) 都有一个被称为容量的权值 \(c_{u, v}\)，对于 \((u, v) \not \in E\)，可以设 \(c_{u, v} = 0\)
\(V\) 中有两个特殊的点：源点（\(s\)），汇点（\(t\)）（\(s \neq t\)）。
流是一个从有序数对 \(u, v\) 映射到实数域 \(\mathbb{R}\) 的函数 \(f(u, v)\)。
网络的性质
-
容量限制：对于所有 \(u, v \in V\)，有 \(0 \leq f(u, v) \leq c(u, v)\)，即每条边的流量必须小于等于这条边的流量。特别的，如果 \(f(u, v) = c(u, v)\)，则称边 \(u, v\) 满流；
-
流量守恒：对于所有 \(i \in V - \{s, t\}\)，有 \(\displaystyle\sum_{u \in V \wedge u \neq i} f(u, i) = \sum_{v \in V \wedge v \neq i} f(i, v)\)，即除了源汇点外的其它点，流入的流量等于流出的流量。而源点可以无限流出流量，汇点可以无限流入流量；
-
斜对称性：\(f(u, v) = -f(v, u)\)，也就是说，\(u\) 到 \(v\) 有 \(f(u, v)\) 的流量，也可以说成是 \(v\) 到 \(u\) 有 \(-f(u, v)\) 的流量。
通俗地讲，在网络中，我们要干的事情是把若干的「流」从 \(s\) 输送到 \(t\)。\(s\) 点只送出流，\(t\) 点只接受流。而中间的点只能用来中转流量。\(c(u, v)\) 限定了 \(u\) 点只能向 \(v\) 点输送的最大流量，因此 \(f(u, v)\)（称作 \((u, v)\) 的流量）不能超过 \(c(u, v)\)。
注意，网络还有一个特殊的性质，那就是如果 \((u, v) \in E\)，那么 \((v, u) \not \in E\)，如果真的出现如图：
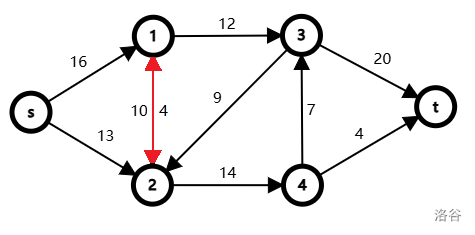
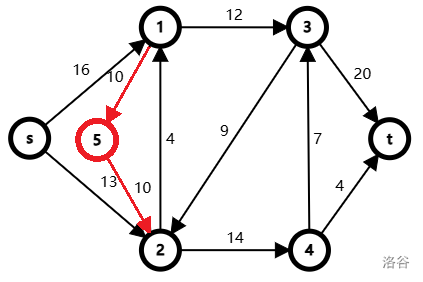
的这种情况，\(1\) 到 \(2\) 的流量为 \(10\)，\(2\) 到 \(1\) 的流量为 \(4\)，那么此时我们只需要新建一个节点 \(5\)，从 \(1\) 到 \(5\) 和从 \(5\) 到 \(2\) 各连一条容量为 \(10\) 的边，就和原网络等价了：
网络最大流
最大流问题是求 \(G\) 上的流 \(f\) 以最大化整个网络的流量 \(|f| = \displaystyle\sum_{v \in V} f(s, v) - \sum_{v \in V} f(v, s)\)。接下来，我们会分别介绍 \(3\) 种方法来解决这个问题。
\(\text{Ford - Fulkerson}\) 方法
残量网络
定义
流了一个流之后，有的边因为有流量，所以还能够的流的量就减少了，同时我们能够选择在这条边上反悔一定的流量，我们将这抽象成残量网络。
设 \(f\) 为流网络 \(G = (V, E)\) 中的一个流，对于节点对 \((u, v)\)，定义其残存容量 \(c_f(u, v)\) 如下：
我们将 \(G\) 中所有结点和剩余容量大于 \(0\) 的边构成的子图称为残量网络 \(G_f\)（\(\text{Residual Network}\)），即 \(G_f = (V, E_f)\)，其中 \(E_f = \{(u, v) \mid c_f(u, v) > 0\}\)。也就是说，将每条边的容量减去流量后，删去流满的边，再连上反向边，就可以得到残量网络。
另外，如果有大小为 \(5\) 的流从 \(u\) 输送到 \(v\)，而同时有大小为 \(7\) 的流从 \(v\) 输送到 \(u\)，这显然没有意义。本质上，只有大小为 \(2\) 的流从 \(v\) 输送到 \(u\)。这就是为什么我们要连反向边。在反向边上推流相当于是把原先推的流给推回去。
残量网络 \(G_f\) 类似于一个容量为 \(c_f\) 的流网络，因此残量网络中也可以定义流，但是针对的容量变成了变成了 \(c_f\)。
我们设 \(f\) 是 \(G\) 中的一个流，\(f'\) 是对应残量网络中的一个流，定义 \(f \uparrow f'\) 为流 \(f'\) 对流 \(f\) 的递增，它是一个从有序数对 \(u, v\) 映射到实数域 \(\mathbb{R}\) 的函数，它的定义如下：
这是很好理解的，根据反向边的作用，往反向边推流等于把原先推过来的流又从新推回去，相当于撤销了推流的操作。
引理 2.4.1
在网络 \(G\) 中，若 \(f\) 是其中一个流，而 \(f'\) 是残量网络 \(G_f\) 上的一个流，那么 \(f \uparrow f'\) 也是 \(G\) 的一个流，而且 \(|f \uparrow f'| = |f| + |f'|\)。
证明：
我们先证明 \(f \uparrow f'\) 满足原网络 \(G\) 中每条边的容量限制，且除了 \(s\) 和 \(t\) 以外，每个节点满足容量守恒的性质。
首先，根据反向边的容量设置，有 \(f'(v, u) \leq c_f(v, u) = f(u, v)\)，那么 \((f \uparrow f')(u, v) = f(u, v) + f'(u, v) - f'(v, u) \geq f(u, v) + f'(u, v) - f(u, v) = f'(u, v) \geq 0\)。
此外，\((f \uparrow f')(u, v) = f(u, v) + f'(u, v) - f'(v, u) \leq f(u, v) + f'(u, v) \leq f(u, v) + c_f(u, v) = c(u, v)\)。因此 \(0 \leq (f \uparrow f')(u, v) \leq c(u, v)\)，那么 \((f \uparrow f')(u, v)\) 是满足容量限制的。
我们再来证明流量守恒。由于 \(f\) 和 \(f'\) 均满足容量守恒，因此对于所有不是 \(s\) 和 \(t\) 的节点 \(u\)，有：
此时 \(f \uparrow f'\) 满足流量守恒，那么 \(f \uparrow f'\) 也是原网络中的一个流。
下面我们再来计算 \(f \uparrow f'\)，根据网络的性质，我们知道 \(G\) 中不存在反向边，因此我们设 \(V_1 = \{v \mid (s, v) \in E\}\)，即有边从源点 \(s\) 到达的节点的集合，\(V_2 = \{v \mid (v, s)\}\)，即有边到达源点的节点集合，那么 \(V_1 \cup V_2 \in V\)，而 \(V_1 \cap V_2 = \emptyset\)，那么 \(|f \uparrow f'| = \displaystyle\sum_{v \in V} (f \uparrow f')(s, v) - \sum_{v \in V} (f \uparrow f')(v, s) = \sum_{v \in V_1} (f \uparrow f')(s, v) - \sum_{v \in V_2} (f \uparrow f')(v, s)\)。
根据 \(f \uparrow f'\) 的定义，我们可以得到：
此时，我们可以将所有和式的下标拓展到 \(V\)，因为不属于 \(V_1\) 的点，\(s\) 没有像它连边，不属于 \(V_1V_2\) 的点，它没有向 \(s\)连边，此时 \(c\) 和 \(c_f\) 都为 \(0\)，那么 \(f\) 和 \(f'\) 也一定为 \(0\)，因此原式最终等于 \(\displaystyle\sum_{v \in V} f(s, v) - \sum_{v \in V} f(v, s) + \sum_{v \in V} f'(s, v) - \sum_{v \in V} f'(v, s) = |f| + |f'|\)
此时我们证明了流的可加性，增加后的流会更接近最大流，这在下一小节很有用处。
增广路与增广
定义
增广路是 \(G_f\) 上一条从源点 \(s\) 到汇点 \(t\) 的路径。对于一条增广路 \(p\)，我们给每一条边 \((u, v) \in p\) 都加上该增广路的残存容量 \(c_f(p) = \min\{c_f(u, v) \mid (u, v) \in p\}\) 以令整个网络的流量增加，这一过程被称为增广（\(\text{Augment}\)）。
引理 2.4.2.1
在网络 \(G\) 中，若 \(f\) 是其中一个流，设 \(p\) 是残量网络 \(G_f\) 中的一条增广路，该增广路的残存容量 \(c_f(p) = \min\{c_f(u, v) \mid (u, v) \in p\}\)，定义一个从有序数对 \(u, v\) 映射到实数域 \(\mathbb{R}\) 的函数 \(f_p(u, v)\) 为：
则 \(f_p\) 是残量网络中的一个流，且 \(f_p = c_f(p) > 0\)。
证明：
这个定理得证明比较简单。首先，既然 \(c_f(p)\) 取的是所有边容量的最小值，那么 \(c_f(p)\) 一定小于等于每条边上的容量限制。而除了源点和汇点以外，由于 \(p\) 是一条路径，那么每个点有一条边进入，必有一条边出去，那么流入和流出的量就是相同的，因此流量守恒。于是 \(f_p\) 是残量网络中的一个流。
现在再来证明 \(f_p = c_f(p)\)，根据整个网络的流量 \(|f| = \displaystyle\sum_{v \in V} f(s, v) - \sum_{v \in V} f(v, s)\)。由于最终要到达 \(t\)，那么 \(p\) 中从 \(s\) 出发的边一定比到达 \(s\) 的边大 \(1\)，那么式子的左边就比式子的右边多了一项，而路径 \(p\) 上每条边的流量都是 \(c_f(p)\)，因此结果就是 \(c_f(p)\)。
于是我们证明了 \(f_p = c_f(p)\)，而由于每条边的残余容量都大于 \(0\)（否则这条路就未联通，不算增广路），因此 \(c_f(p) > 0\)，于是我们证明了引理。
推论 2.4.2.2
在网络 \(G\) 中，若 \(f\) 是其中一个流，设 \(p\) 是残量网络 \(G_f\) 中的一条增广路，\(f_p\) 的定义如上，那么如果将 \(f\) 增加 \(f_p\)，则 \(f \uparrow f'\) 是 \(G\) 中的一个流，且 \(|f \uparrow f_p| = |f| + |f_p| \geq |f|\)。
可以通过引理 2.4.1 和引理 2.4.2.1 立即证明。
此时我们证明了不断找增广路更新最大流会使最大流单增，不断靠近真正的最大流，这就叫做 \(\text{Ford - Fulkerson}\) 方法，后面的 \(\text{Edmonde - Karp}\)、\(\text{Dinic}\) 和 \(\text{ISAP}\) 算法都基于这种思路。
割
定义
网络的一个割将顶点集合 \(V\) 划分成 \(S\) 和 \(T = V - S\) 两个集合，使得 \(s \in S\) 且 \(t \in T\)。若 \(f\) 是一个流，则定义横跨割的净流量 \(f(S, T) = \displaystyle\sum_{u \in S} \sum_{v \in T} f(u, v) - \sum_{u \in S} \sum_{v \in T} f(v, u)\)，而割 \((S, T)\) 的容量则被定义成 \(c(S, T) = \displaystyle\sum_{u \in S} \sum_{v \in T} c(u, v)\)。
一个网络的最小割是整个网络中容量最小的割。
引理 2.4.3.1
设 \(f\) 为网络 \(G\) 中的一个流，\((S, T)\) 为网络中一个任意的割，则横跨割 \((S, T)\) 的净流量为 \(f(S, T) = |f|\)。
证明：
根据容量守恒，对于不是源点和汇点的节点 \(u\)，我们有 \(\displaystyle\sum_{v \in V} f(u, v) - \sum_{v \in V} f(v, u) = 0\)。
由于 \(S\) 中除 \(s\) 外每个点都满足容量守恒，因此
由于 \(S \cup T = v\) 且 \(S \cap T = \emptyset\)，于是我们将 \(V\) 拆分成 \(S\) 和 \(T\) 两部分分别求和：
引理证明成立。此时我们知道了一个流会与一个割相互对应。
推论 2.4.3.2
网络 \(G\) 中任意流 \(f\) 的值不能超过网络中任意割的容量。
证明：
根据引理 2.4.3.1，我们知道 \(|f| = f(S, T) = \displaystyle\sum_{u \in s} \sum_{v \in T} f(u, v) - \sum_{u \in s} \sum_{v \in T} f(v, u) \leq \sum_{u \in s} \sum_{v \in T} f(u, v) \leq \sum_{u \in s} \sum_{v \in T} c(u, v) = c(S, T)\)。
推论证明成立，此时我们可以得出网络最大流的值不能超过网络的最小割的容量，其实网络最大流的值就等于网络的最小割的值，这就是下一个定理。
定理 2.3.3.3（最大流最小割定理）
这是整个网络流中最重要的定理，一切网络流算法的正确性都由该定理保证。
设 \(f\) 为网络 \(G\) 中的一个流，那么以下条件是等价的：
-
\(f\) 是 \(G\) 的一个最大流；
-
残量网络 \(G_f\) 中不包含任何增广路；
-
\(|f| = c(S, T)\)，其中 \(c(S, T)\) 为网络 \(G\) 的最小割的容量。
证明：
先证明 \(1\) 可以推出 \(2\)，考虑反证法。
假设 \(f\) 是 \(G\) 的一个最大流，但残量网络 \(G_f\) 中还包含一条增广路 \(p\)，那么根据推论 2.4.2.2，\(|f \uparrow f_p| > |f|\)，这与 \(f\) 是 \(G\) 的一个最大流相矛盾。因此 \(1\) 可以推到 \(2\)。
现在再来证明 \(2\) 可以推到 \(3\)。由于 \(1\) 和 \(2\) 是等价的，因此此时残量网络 \(G_f\) 中不存在任何一条增广路，于是我们定义 \(S\) 为 \(V\) 中能被 \(S\) 到达的点构成的集合，\(T = V - S\)，显然 \(s \in S\)，而 \(t \not \in S\)，那么 \((S, T)\) 就是原先的网络 \(G\) 的一个割。
现在考虑一对节点 \(u \in S\) 和 \(v \in T\)，如果 \((u, v) \in E\)，由于已经不存在增广路，因此 \(f(u, v) = c(u, v)\)。而如果 \((v, u) \in E\)，那么 \(f(v, u) = 0\)，否则 \(c_f(u, v) = f(v, u)\) 将为正值，那么边 \((u, v)\) 会出现在残量网络 \(G_f\) 中，那么 \(v\) 也因该属于 \(S\)，矛盾。因此 \(f(S, T) = \displaystyle\sum_{u \in S} \sum_{v \in T} f(u, v) - \sum_{v \in T} \sum_{u \in S} f(v, u) = \sum_{u \in S} \sum_{v \in T} c(u, v) - \sum_{v \in T} \sum_{u \in S} 0 = c(S, T)\)，而根据推论 2.4.3.2，网络 \(G\) 中任意的流 \(f\) 不会超过任意的割的容量，那么网络 \(G\) 的最大流的值只能等于网络 \(G\) 的最小割的容量。因此 \(2\) 可以推到 \(3\)。
我们最后来证明 \(3\) 可以推到 \(1\)。根据推论 2.4.3.2，\(|f| \leq c(S, T)\)，因此 \(|f|\) 的上界就是网络 \(G\) 的最小割的容量，因此此时 \(f\) 是网络 \(G\) 的最大流。
三个条件可以互相推导，因此定理 2.4.3.3 成立。
此时我们就可以不断在残量网络中找增广路来更新最大流，直到找不到增广路为止，此时的流就是最大流了。以下是这种思路的几种具体实现。
\(\text{Edmonde - Karp}\) 算法
算法实现
\(\text{Edmonde - Karp}\) 算法的核心是用 BFS 找长度最短的增广路，每次我们找到这样一条增广路，就从 \(s\) 反推回 \(t\)，并更新每条边的剩余容量。
完整代码：洛谷 P3376 【模板】网络最大流
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e2 + 9, M = 5e3 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int fl[N], fr[N];
int maxflow(int s, int t){
int flow = 0;
while(true){
queue <int> q;
memset(fl, -1, sizeof(fl));
fl[s] = 1e18;
q.push(s);
while(!q.empty()){
int u = q.front();
q.pop();
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(e[i].c && fl[v] == -1){
fl[v] = min(e[i].c, fl[u]);
fr[v] = i;
q.push(v);
}
}
}
if(fl[t] == -1)
return flow;
flow += fl[t];
for(int u = t; u != s; u = e[fr[u] ^ 1].v){
e[fr[u]].c -= fl[t];
e[fr[u] ^ 1].c += fl[t];
}
}
}
int n, m, s, t;
signed main(){
scanf("%lld%lld%lld%lld", &n, &m, &s, &t);
for(int i = 1; i <= m; i++) {
int u, v, c;
scanf("%lld%lld%lld", &u, &v, &c);
addEdge(u, v, c);
addEdge(v, u, 0);
}
printf("%lld", maxflow(s, t));
return 0;
}
复杂度分析
\(\text{Edmonde - Karp}\) 算法时间复杂度的保证在于每次找的是长度最短的增广路，我们来看看它的原因。
先定义，残量网络 \(G_f\) 中从节点 \(u\) 到节点 \(v\) 的最短路径长度（忽视容量）为 \(\delta_f(u, v)\)。
引理 2.4.4.2.1
在网络 \(G\) 中，如果运行 \(\text{Edmonde - Karp}\) 算法，则在残量网络 \(G_f\) 中，对于所有节点 \(u \in V - \{s\}\)，\(\delta_f(s, v)\) 随着每次流量的递增而单增。
证明：
考虑反证法。
我们假设对于某个节点 \(v \in V - \{s\}\)，存在一个使流量增加的操作，导致节点 \(s\) 到节点 \(v\) 的最短路径距离减小。设 \(f\) 为出现这种变化前的流量，\(f'\) 为出现这种变化之后的流量。设 \(v\) 是所有在本次增流中与 \(s\) 的距离减小的点中，\(\delta_{f'} (s, v)\) 最小的节点，因此 \(\delta_{f'}(s, v) < \delta_f(s, v)\)。设 \(p = s \leadsto u \rightarrow v\) 为残量网络 \(G_{f'}\) 上从源点 \(s\) 到节点 \(v\) 的一条最短路径，显然，\(\delta_{f'}(s, u) = \delta_{f'}(s, v) - 1\)。
由于 \(v\) 已经是本次增流中与 \(s\) 的距离减小的点中，\(\delta_{f'}(s, v)\) 最小的节点，而 \(\delta_{f'}(s, u) < \delta_{f'}(s, v)\)，那么 \(u\) 到 \(s\) 的距离一定没有减少，那么 \(\delta_{f'}(s, u) \geq \delta_f(s, u)\)。
此时我们一定知道 \((u, v)\) 不在残量网络 \(G_f\) 中，否则：
（第一个不等式就是差分约束时我们求出的 \(dis_v \leq dis_u + w_{u, v}\)）
此时与我们的假设 \(\delta_{f'}(s, v) < \delta_f(s, v)\) 相矛盾。
但是，由于在残量网络 \(G_{f'}\) 中，从 \(u\) 可以走到 \(v\)，那么 \((u, v)\) 一定在残量网络 \(G_{f'}\) 中，而 \((u, v)\) 并不在残量网络 \(G_f\) 中，因此本次推流操作一定增加了 \(v\) 到 \(u\) 的流量，此时就会建上反向边。由于 \(\text{Edmonde - Karp}\) 算法每次都找最短路增广，因此在残量网络 \(G_f\) 中，\(s\) 到 \(u\) 的最短路一定是 \(s \leadsto v \rightarrow u\)，那么：
这又与我们的假设 \(\delta_{f'}(s, v) < \delta_f(s, v)\) 相矛盾。因此我们最终推出对于所有节点 \(u \in V - \{s\}\)，\(\delta_f(s, v)\) 随着每次流量的递增而单增。
定理 2.4.4.2.2
在网络 \(G\) 中，如果运行 \(\text{Edmonde - Karp}\) 算法，那么该算法的增广次数为 \(O(VE)\)。
证明：
我们新定义，在残量网络 \(G_f\) 中，如果一条增广路的残存容量等于该路径上 \((u, v)\) 这条边的残存容量，那么就称 \((u, v)\) 为增广路 \(p\) 上的关键边，在沿一条增广路推流后，该增广路上所有关键边都会消失，但是会生成反边，当再次增广时，如果反向边被推流，那么又会从新生成原来的边，又有可能成为关键边，但是一条边成为关键边的次数也是有上限的。
设 \((u, v) \in E\)，由于 \(\text{Edmonde - Karp}\) 每次都找最短路增广，那么当 \((u, v)\) 第一次成为关键边时，有 \(\delta_f(s, v) = \delta_f(s, u) + 1\)。一旦进行推流操作，这条边就会消失，直到出现之前所说的反向边被推流的情况出现，也就是 \(f(u, v)\) 减少时，\((u, v)\) 才会出现，如果这种情况出现时 \(f'\) 是目前求出的流，那么 \(\delta_{f'}(s, u) = \delta_{f'}(s, v) + 1\)，而根据引理 2.4.4.2.1，\(\delta_f(s, v) \leq \delta_{f'}(s, v)\)，那么 \(\delta_{f'}(s, u) = \delta_{f'}(s, v) + 1 \geq \delta_f(s, v) + 1 = \delta_f(s, u) + 2\)。
因此，从边 \((u, v)\) 成为关键边到下一次成为关键边，\(s\) 到 \(u\) 的距离至少增加了 \(2\)，而 \(s\) 到 \(u\) 的初始距离一定大于等于 \(0\)，考虑到从 \(s\) 到 \(u\) 的路径上不可能再经过 \(s, u\) 和 \(t\)（前两个显然，不可能经过 \(t\) 是因为 \((u, v)\) 在增广路上），因此，直到 \(u\) 变得不可到达之前，\(s\) 和 \(u\) 的最短距离最多是 \(|V| - 2\)，而成为一次关键边，最短距离至少变大 \(2\)，那么 \((u, v)\) 至多只会成为 \(O(V)\) 次关键边。由于一共有 \(O(E)\) 条边可能成为关键边，那么一共会有 \(O(VE)\) 个关键边，而每条增广路至少有一条关键边，因此定理成立。
用 BFS 寻找增广路时，最多会进行 \(O(E)\) 次迭代，因此 \(\text{Edmonde - Karp}\) 算法的时间复杂度为 \(O(VE^2)\)。
\(\text{Dinic}\) 算法
算法实现
我们考虑 \(\text{Edmonde - Karp}\) 算法比较缓慢的原因，那就是每次都要重新找一条从 \(s\) 到 \(t\) 的增广路。我们能不能一次 BFS 就找到多条增广路呢？这就是 \(\text{Dinic}\) 算法的思想。我们 BFS 一张图的时候，如果一个点有分叉，那么就把当前流 \(f\) 往每条路径都推一次流，具体实现如下：
-
BFS 用于给图分层，限制 DFS 的搜索范围，使得 DFS 不会绕圈子，因此在分层图中找到的每一条路径都是最短的，符合 \(\text{Edmonde - Karp}\) 算法的设计；
-
DFS 用于增广，当从点 \(u\) 的某个分支往下 DFS 找到一条增广路后，就不断回溯并更新路径上边的容量，使得后面再做 DFS 时容量是正确的。
\(\text{Dinic}\) 算法有两个优化，如下：
-
对增广完毕的剪枝。当从一个点 \(u\) DFS 时，如果可以往后推的流为 \(0\)，那么以后也无法从 \(u\) 继续推流，因此就将其删去；
-
当前弧优化。当 DFS 遍历当前点 \(u\) 的第 \(i\) 条分支时，前 \(i - 1\) 条分支已经无法继续推流了，下一次访问到 \(u\) 时就可以从第 \(i\) 条分支开始。
完整代码：洛谷 P3376 【模板】网络最大流
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e2 + 9, M = 5e3 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, s, t;
bool bfs(){
for(int i = 1; i <= n; i++)
dep[i] = INF;
queue <int> q;
q.push(s);
dep[s] = 0;
while(!q.empty()){
int u = q.front();
q.pop();
cur[u] = head[u];
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(dep[v] == INF && e[i].c > 0){
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return dep[t] != INF;
}
int dfs(int u, int flow){
if(u == t)
return flow;
int res = 0;
for(int &i = cur[u]; i; i = e[i].nex){
int v = e[i].v, k;
if(e[i].c > 0 && dep[v] == dep[u] + 1 && (k = dfs(v, min(e[i].c, flow)))){
res += k;
flow -= k;
e[i].c -= k;
e[i ^ 1].c += k;
if(!flow)
return res;
}
}
if(!res)
dep[u] = INF;
return res;
}
int ans;
signed main(){
scanf("%lld%lld%lld%lld", &n, &m, &s, &t);
for(int i = 1; i <= m; i++){
int u, v, w;
scanf("%lld%lld%lld", &u, &v, &w);
addEdge(u, v, w);
addEdge(v, u, 0);
}
while(bfs())
ans += dfs(s, INF);
printf("%lld", ans);
return 0;
}
复杂度分析
有了 \(\text{Edmonde - Karp}\) 算法的复杂度证明，\(\text{Dinic}\) 的时间复杂度就比较容易证得了。
由于 \(\text{Dinic}\) 算法是先分层再 DFS，因此我们需要关注图中最长的最短路的长度，而由于每次最长的最短路长度都会增加，而最短路上最多有 \(O(V)\) 个点，因此 Dinic 会进行 \(O(V)\) 次增广。
我们现在来证明单次增广的复杂度是 \(O(VE)\) 的，且上界非常松。
对于那些流满的边，当前弧优化会花费 \(O(m)\) 的时间复杂度跳过他们。而我们用 DFS 搜索一条增广路的时间复杂度是 \(O(n)\)（其实远达不到，除非几乎所有增广路都没有公共边）。找到增广路后，我们回溯至增广路上第一条关键边（因为没有剩余流量了），并将所有关键边的流量置为零。这些关键边会在第二次遍历到时被当前弧优化直接跳过，这部分，即跳过已经作为某次增广的关键边的边的总复杂度就是当前弧优化的 \(O(m)\)，因此，增广一次再回溯的时间复杂度为 \(O(VE)\)，那么总复杂度就是 \(O(V^2E)\)，且常数应该比 \(1\) 还小。
\(\text{ISAP}\) 算法
推送-重贴标签算法
现在抛开前面讲的所有残量网络、增广路、割及其一系列定理，我们换一个角度思考网络最大流问题。
高度函数
推送
重贴标签
通用推送-重贴标签算法
最高标推送-重贴标签（\(\text{HLPP}\)） 算法
完整代码：洛谷 P4722 【模板】最大流 加强版 / 预流推进
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1.2e4 + 9, M = 1.2e5 + 9;
struct Edge{
int v, f, nex;
} e[M << 2];
int head[N], ecnt = 1;
void addEdge(int u, int v, int f){
e[++ecnt] = Edge{v, f, head[u]};
head[u] = ecnt;
}
int h[N], E[N], gap[N], n, m, s, t;//h[i]表示一个点的高度，E[i]表示一个点的超额流，gap[i]为优化数组
bool inq[N];
struct cmp{
bool operator ()(int x, int y) const{
return h[x] < h[y];
}
};
priority_queue <int, vector<int>, cmp> p;
queue <int> q;
bool bfs(){
memset(h, 0x3f3f, sizeof(h));
h[t] = 0;
q.push(t);//从汇点往上回溯
while(!q.empty()){
int u = q.front();
q.pop();
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(e[i ^ 1].f && h[v] > h[u] + 1){//如果v的流量还有剩余，且v的高度比u高，就可以将v中存储的水推向u
h[v] = h[u] + 1;//更新高度，让之后的点更有机会推流
q.push(v);
}
}
}
return h[s] != 0x3f3f3f3f3f3f3f3f;//判断源点是否联通
}
void push(int u){//推送操作
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(e[i].f && h[u] == h[v] + 1){//可以往v推流
int f = min(e[i].f, E[u]);//找到最大可以推向v的水量
e[i].f -= f;//这条边的流量减小
e[i ^ 1].f += f;//用于反悔的边流量增加
E[u] -= f;//u点的超额流减小
E[v] += f;//v点的超额流增加
if(v != s && v != t && !inq[v]){//更新其它点
p.push(v);//按照高度排序
inq[v] = true;
}
if(!E[u])
break;
}
}
}
void relabel(int u){//重贴标签操作
h[u] = 0x3f3f3f3f3f3f3f3f;
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(e[i].f && h[u] > h[v] + 1)//找到一个高度使得h[u]比h[v]大，u可以往v推流，且最小
h[u] = h[v] + 1;//更新高度
}
}
int HLPP(){
if(!bfs())//s和t不连通，最大流为0
return 0;
h[s] = n;
for(int i = 1; i <= n; i++)
if(h[i] < 0x3f3f3f3f3f3f3f3f)
gap[h[i]]++;
for(int i = head[s]; i; i = e[i].nex){//先推一遍
int v = e[i].v;
if(e[i].f && h[v] < 0x3f3f3f3f3f3f3f3f){
int f = e[i].f;
e[i].f -= f;
e[i ^ 1].f += f;
E[s] -= f;
E[v] += f;
if(v != s && v != t && !inq[v]){
p.push(v);
inq[v] = true;
}
}
}
while(!p.empty()){
int u = p.top();
inq[u] = false;
p.pop();
push(u);//往下推流
if(E[u]){//还有剩余的超额流
gap[h[u]]--;
if(!gap[h[u]])//优化二
for(int i = 1; i <= n; i++)
if(i != s && i != t && h[i] > h[u] && h[i] < n - 1)
h[i] = n + 1;
relabel(u);//调整高度来推送剩下的超额流
gap[h[u]]++;
p.push(u);
inq[u] = true;
}
}
return E[t];
}
signed main(){
scanf("%lld%lld%lld%lld", &n, &m, &s, &t);
for(int i = 1; i <= m; i++){
int u, v, f;
scanf("%lld%lld%lld", &u, &v, &f);
addEdge(u, v, f);
addEdge(v, u, 0);
}
printf("%lld", HLPP());
return 0;
}
费用流
现在流网络 \(G = (V, E)\) 中每条边除了容量 \(c(u, v)\)，还有多了一个单位费用 \(w(u, v)\)（\(w\) 也满足斜对称性，也就是 \(w(u, v) = -w(v, u)\)），一条边费用为 \(f(u, v) \times w(u, v)\)，整个网络的总费用就是每一条边费用的总和。
则该网络中使得总费用最小的那个最大流就被称作最小费用最大流，即满足 \(\displaystyle\sum_{v \in V} f(s, v) - \sum_{v \in V} f(v, s)\) 最大的前提下，最小化 \(\displaystyle\sum_{u \in V} \sum_{v \in V} f(u, v) \times c(u, v)\)。
\(\text{SSP}\) 算法
这个算法的思路非常简单，就是把求最大流时用的 BFS 换成了 SPFA，每次找费用最小的增广路来增广，不过它只能用来处理没有负环的网络。下面我们来证明这是正确的。
首先，根据推出的最大流最小割定理，不断在残量网络上找增广路来更新答案一定可以求出最大流，那我们只用证明这样做的费用是最小的。
考虑数学归纳法，假设流量为 \(i\) 时最小花费为 \(i\)，由于图中不存在负环，因此 \(f_0 = 0\)。此时 \(\text{SSP}\) 算法什么事也没干，因此边界条件是符合的。
假设用 \(\text{SSP}\) 求出来的流量为 \(i\) 时的最小花费就是 \(f_i\)，此时我们在残量网络中找到了费用最小的增广路并求出了 \(f_{i + 1}\)，那么 \(\Delta f = f_{i + 1} - f_i\) 就是这条增广路的费用。
假设存在一个更小的 \(f'_{i + 1}\)，因为 \(\Delta f\) 已经是费用最小的增广路了，那么 \(f'_{i + 1} - f_i\) 的花费所对应的增广路一定经过了负环。但是如果存在负环，那么在求 \(f_i\) 时就可以往负环推入一定量的流，由于是环，一定满足流量守恒，但这时的费用已经减小了，因此 \(f_i\) 就不是花费最小的流量为 \(i\) 的流。因此不存在一个更小的 \(f'_{i + 1}\)，符合数学归纳法，证明成立。
不过有一点，SPFA 每次是找费用最小的增广路，那么有可能增广的流的大小一直为 \(1\)，因此总复杂度是 \(O(nm |f|)\) 的，而 \(|f|\) 可能很大，达到 \(2^{\frac n2}\)，此时总时间复杂度为 \(O(n^3 2^{\frac n2})\)，因此 \(\text{SSP}\) 为伪多项式复杂度的。
完整代码：洛谷 P3381 【模板】最小费用最大流
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 5e3 + 9, M = 5e4 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, w, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int w){
e[++ecnt] = Edge{v, c, w, head[u]};
head[u] = ecnt;
}
int cur[N], dis[N], n, m, s, t;
queue <int> q;
bool inq[N];
bool spfa(){
for(int i = 1; i <= n; i++){
dis[i] = INF;
}
q.push(s);
inq[s] = true;
dis[s] = 0;
while(!q.empty()){
int u = q.front();
q.pop();
cur[u] = head[u];
inq[u] = false;
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(e[i].c > 0 && dis[v] > dis[u] + e[i].w){
dis[v] = dis[u] + e[i].w;
if(!inq[v]){
q.push(v);
inq[v] = true;
}
}
}
}
return dis[t] != INF;
}
bool vis[N];
pii dfs(int u, int flow){
if(u == t)
return mk(flow, 0);
int res = 0, val = 0;
vis[u] = 1;
for(int &i = cur[u]; i; i = e[i].nex){
int v = e[i].v;
if(!vis[v] && dis[v] == dis[u] + e[i].w && e[i].c){
pii k = dfs(v, min(e[i].c, flow));
if(!k.first)
continue;
res += k.first;
flow -= k.first;
val += e[i].w * k.first + k.second;
e[i].c -= k.first;
e[i ^ 1].c += k.first;
if(!flow)
break;
}
}
vis[u] = 0;
if(!res){
dis[u] = INF;
}
return mk(res, val);
}
int ans, res;
signed main(){
scanf("%lld%lld%lld%lld", &n, &m, &s, &t);
for(int i = 1; i <= m; i++){
int u, v, c, w;
scanf("%lld%lld%lld%lld", &u, &v, &c, &w);
addEdge(u, v, c, w);
addEdge(v, u, 0, -w);
}
while(spfa()){
pii tmp = dfs(s, INF);
ans += tmp.first;
res += tmp.second;
}
printf("%lld %lld", ans, res);
return 0;
}
\(\text{Primal-Dual}\) 原始对偶算法
完整代码：洛谷 P3381 【模板】最小费用最大流
消圈算法
上下界网络流
上下界网络流较初始网络 \(G\)，每条边上还多了一个流量下界 \(b_{u, v}\)，也就是在保证流量守恒的前提下，每条边的流量 \(f_{u, v}\) 还要满足 \(b_{u, v} \leq f_{u, v} \leq c_{u, v}\)，这使得流量限制更加严格，后面有些复杂的网络流建模的题目都可以用上下界网络流无脑切掉。
无源汇上下界可行流
这是整个上下界网络流的基础。此时整个网络中都不存在源点 \(s\) 和汇点 \(t\)，因此每一个点都要保证流量守恒。
解决这类问题的通用方法是，先满足流量下界 \(b(u, v)\)，不过此时流量并没有守恒，于是我们计算出一个点 \(u\) 的净流量 \(w_u = \displaystyle\sum_{v \in V} f(u, v) - \sum_{v \in V} f(v, u)\)，如果 \(w_u > 0\)，说明流入 \(u\) 的流量太多了，需要流出，反之则需要流入。此时满足了流量下界的要求，因此我们从新设 \(c(u, v) = c(u, v) - b(u, v)\)，转化为一个普通网络流问题。
此时我们考虑在原图上建出超级源点 \(S\) 和超级汇点 \(T\)，如果 \(w_u > 0\)，就从 \(S\) 网 \(u\) 连一条边，如果 \(w_u < 0\)，就从 \(u\) 像 \(T\) 连一条边。跑一边普通的网络最大流。这样除 \(S\) 和 \(T\) 外每个点都流量守恒了，此时如果从 \(S\) 出发的每一条边 \((S, u)\) 都流满了，证明 \(u\) 可以将多流入的这 \(w_u\) 的流流出去，对 \(T\) 也是一样的道理。也就是说，如果最大流正好等于 \(\displaystyle\sum_{w_u > 0} w_u\)（由于斜对称性，\(\displaystyle\sum_{w_u > 0} w_u = \displaystyle\sum_{w_u < 0} w_u\)，因此求二者皆可），那么就存在一种满足上下界的可行流，反之就不存在。
完整代码：LOJ115 无源汇有上下界可行流
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e2 + 9, M = 2e4 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, b, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int b){
e[++ecnt] = Edge{v, c, b, head[u]};
head[u] = ecnt;
}
int fl[N], cur[N], dep[N], n, m, s, t;
bool bfs(){
for(int i = 1; i <= n; i++)
dep[i] = INF;
queue <int> q;
q.push(s);
dep[s] = 0;
while(!q.empty()){
int u = q.front();
q.pop();
cur[u] = head[u];
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(dep[v] == INF && e[i].c > 0){
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return dep[t] != INF;
}
int dfs(int u, int flow){
if(u == t)
return flow;
int res = 0;
for(int &i = cur[u]; i; i = e[i].nex){
int v = e[i].v, k;
if(e[i].c > 0 && dep[v] == dep[u] + 1 && (k = dfs(v, min(e[i].c, flow)))){
res += k;
flow -= k;
e[i].c -= k;
e[i ^ 1].c += k;
if(!flow)
return res;
}
}
if(!res)
dep[u] = INF;
return res;
}
int ans, sum;
signed main(){
scanf("%lld%lld", &n, &m);
s = n + 1, t = n + 2;
n += 2;
for(int i = 1; i <= m; i++){
int u, v, b, c;
scanf("%lld%lld%lld%lld", &u, &v, &b, &c);
fl[u] -= b;
fl[v] += b;
addEdge(u, v, c - b, b);
addEdge(v, u, 0, b);
}
for(int i = 1; i <= n; i++){
if(fl[i] > 0){
sum += fl[i];
addEdge(s, i, fl[i], 0);
addEdge(i, s, 0, 0);
}
if(fl[i] < 0){
addEdge(i, t, -fl[i], 0);
addEdge(t, i, 0, 0);
}
}
while(bfs())
ans += dfs(s, INF);
if(ans != sum)
printf("NO");
else {
printf("YES\n");
for(int i = 2; i <= 2 * m; i += 2)
printf("%lld\n", e[i].b + e[i ^ 1].c);
}
return 0;
}
有源汇上下界可行流
从 \(t\) 往 \(s\) 连一条下界为 \(0\)，上界为 \(\infty\) 的边，然后转化成无源汇上下界可行流，注意分清楚源汇点和超级源汇点。
有源汇上下界最大流
我们先求解出一组可行解，由于最大流有反悔操作，因此无论初始的 \(f\) 是什么样的，只要它合法，我们一定可以通过 \(\text{Dinic}\) 求出最大流。我们只需要把超级源汇点 \(S, T\) 删去，将 \(t\) 到 \(u\) 连的边删去。继续在残量网络中跑一遍网络最大流就可以了。
注意，判断是否存在可行流时，比较的是 \(S\) 到 \(T\) 的流量，而在有源汇网络中可行流的大小是 \(s\) 到 \(t\) 连的反边的容量，一定要注意。
完整代码：LOJ116 有源汇有上下界最大流
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e2 + 9, M = 2e4 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, b, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int b){
e[++ecnt] = Edge{v, c, b, head[u]};
head[u] = ecnt;
}
int fl[N], cur[N], dep[N], n, m, ss, tt, S, T;
bool bfs(int s, int t){
for(int i = 1; i <= n; i++)
dep[i] = INF;
queue <int> q;
q.push(s);
dep[s] = 0;
while(!q.empty()){
int u = q.front();
q.pop();
cur[u] = head[u];
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(dep[v] == INF && e[i].c > 0){
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return dep[t] != INF;
}
int dfs(int u, int t, int flow){
if(u == t)
return flow;
int res = 0;
for(int &i = cur[u]; i; i = e[i].nex){
int v = e[i].v, k;
if(e[i].c > 0 && dep[v] == dep[u] + 1 && (k = dfs(v, t, min(e[i].c, flow)))){
res += k;
flow -= k;
e[i].c -= k;
e[i ^ 1].c += k;
if(!flow)
return res;
}
}
if(!res)
dep[u] = INF;
return res;
}
int Dinic(int s, int t){
int res = 0;
while(bfs(s, t))
res += dfs(s, t, INF);
return res;
}
int ans, sum;
signed main(){
scanf("%lld%lld%lld%lld", &n, &m, &ss, &tt);
S = n + 1, T = n + 2;
n += 2;
for(int i = 1; i <= m; i++){
int u, v, b, c;
scanf("%lld%lld%lld%lld", &u, &v, &b, &c);
fl[u] -= b;
fl[v] += b;
addEdge(u, v, c - b, b);
addEdge(v, u, 0, b);
}
for(int i = 1; i <= n; i++){
if(fl[i] > 0){
sum += fl[i];
addEdge(S, i, fl[i], 0);
addEdge(i, S, 0, 0);
}
if(fl[i] < 0){
addEdge(i, T, -fl[i], 0);
addEdge(T, i, 0, 0);
}
}
addEdge(tt, ss, INF, 0);
addEdge(ss, tt, 0, 0);
ans = Dinic(S, T);
if(ans != sum)
printf("please go home to sleep");
else {
ans = e[ecnt].c;
n -= 2;
head[ss] = e[head[ss]].nex;
head[tt] = e[head[tt]].nex;
for(int i = 1; i <= n; i++)
if(fl[i])
head[i] = e[head[i]].nex;
ans += Dinic(ss, tt);
printf("%lld", ans);
}
return 0;
}
有源汇上下界最小流
根据 \(s\) 到 \(t\) 的最小流流量等于 \(t\) 到 \(s\) 的最大流流量相反数这一性质，直接用可行流流量减去 \(t\) 到 \(s\) 的最大流流量即可。
完整代码：LOJ117 有源汇有上下界最小流
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e4 + 9, M = 2e5 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, b, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int b){
e[++ecnt] = Edge{v, c, b, head[u]};
head[u] = ecnt;
}
int fl[N], cur[N], dep[N], n, m, ss, tt, S, T;
bool bfs(int s, int t){
for(int i = 1; i <= n; i++)
dep[i] = INF;
queue <int> q;
q.push(s);
dep[s] = 0;
while(!q.empty()){
int u = q.front();
q.pop();
cur[u] = head[u];
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(dep[v] == INF && e[i].c > 0){
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return dep[t] != INF;
}
int dfs(int u, int t, int flow){
if(u == t)
return flow;
int res = 0;
for(int &i = cur[u]; i; i = e[i].nex){
int v = e[i].v, k;
if(e[i].c > 0 && dep[v] == dep[u] + 1 && (k = dfs(v, t, min(e[i].c, flow)))){
res += k;
flow -= k;
e[i].c -= k;
e[i ^ 1].c += k;
if(!flow)
return res;
}
}
if(!res)
dep[u] = INF;
return res;
}
int Dinic(int s, int t){
int res = 0;
while(bfs(s, t))
res += dfs(s, t, INF);
return res;
}
int ans, sum;
signed main(){
scanf("%lld%lld%lld%lld", &n, &m, &ss, &tt);
S = n + 1, T = n + 2;
n += 2;
for(int i = 1; i <= m; i++){
int u, v, b, c;
scanf("%lld%lld%lld%lld", &u, &v, &b, &c);
fl[u] -= b;
fl[v] += b;
addEdge(u, v, c - b, b);
addEdge(v, u, 0, b);
}
for(int i = 1; i <= n; i++){
if(fl[i] > 0){
sum += fl[i];
addEdge(S, i, fl[i], 0);
addEdge(i, S, 0, 0);
}
if(fl[i] < 0){
addEdge(i, T, -fl[i], 0);
addEdge(T, i, 0, 0);
}
}
addEdge(tt, ss, INF, 0);
addEdge(ss, tt, 0, 0);
ans = Dinic(S, T);
if(ans != sum)
printf("please go home to sleep");
else {
ans = e[ecnt].c;
n -= 2;
head[ss] = e[head[ss]].nex;
head[tt] = e[head[tt]].nex;
for(int i = 1; i <= n; i++)
if(fl[i])
head[i] = e[head[i]].nex;
ans -= Dinic(tt, ss);
printf("%lld", ans);
}
return 0;
}
有源汇上下界费用流
我们一般解决的问题为有源汇上下界最小费用可行流。
我们依然考虑和有源汇上下界可行流的思路，我们将一条边 \((u, v)\) 的流量从新设为 \(c(u, v) - b(u, v)\)，此时我们在新图上跑一边普通的最小费用最大流，由于下界的费用一定是要满足的，而跑最小费用最大流又求出了新增流量的最小费用，因此可以求出最小费用。
网络流模型总结
限制流量
如果一张图拥有多个源点，每个源点流出的流量有限制，那么就从超级源点连一条流量为限制的边；如果一张图拥有多个汇点，每个汇点流入的流量有限制，那么就从该店向超级汇点连一条流量为限制的边。
拆点 / 拆边
拆点的情况比较少，那就是如果一个点只能经过 \(k\) 次，那么就将这一个点拆成入点（我一般设为 \(n + 1 \sim 2 \times n\)）和出点（我一般设为 \(1 \sim n\)），从入点往出点连一条流量为 \(k\) 的边，如果一个点还有点权 \(c\)，那么就在把这条边的费用设为 \(c\)。
拆边一般是以下两种情况：
-
一条边 \((u, v)\) 允许经过多次，但费用 \(c\) 只算一次，那么就从 \(u\) 向 \(v\) 先连一条费用为 \(c\)，流量为 \(1\) 的边，再从 \(u\) 向 \(v\) 连一条费用为 \(0\)，流量为 \(\infty\) 的边；
-
当一条 \((u, v)\) 边产生的费用不再是流量乘以单位费用时，如果这条边流量增加 \(1\)，费用的增加量满足某个公式时，那么我们可以从 \(u\) 向 \(v\) 连 \(c_{u, v}\) 条重边，每条边的容量为 \(1\)，费用为 \(w_f - w_{f - 1}\)。此时假设流了 \(f\) 的流，那么费用就是 \(w_f\) 了。
最小割（集合划分）模型
鱼，我所欲也；熊掌，亦我所欲也。二者不可得兼，舍鱼而取熊掌者也。生，亦我所欲也；义，亦我所欲也。二者不可得兼，舍生而取义者也。——《孟子 \(\cdot\) 告子上》
如果一个元素可以放在两个不同的集合中，放在每个集合中都有对应的贡献，但是不能同时放在两个集合中。或者选了某个数，与它有某种关系的数都无法选择时，我们必须舍弃一部分权值，我们肯定希望损失的权值尽可能小。此时就需要用到最小割模型了。
形式化的，有两个集合 \(A\) 和 \(B\)，我们需要把 \(u \in [1, n]\) 放入两个集合中的一个。设 \(a_u\) 为 \(u\) 不放在 \(A\) 中损失的权值，\(b_u\) 为不放在 \(B\) 中损失的权值，\(w_{u, v}\) 为 \(u, v\) 不放在一个集合中损失的权值。现在，我们需要最小化 \(\displaystyle\min_{x_1, x_2, \dots, x_n} \sum_{(u, v) \in E} w_{u, v} x_u \overline{x_v} + \displaystyle\sum_u a_u x_u + b_u \overline{x_u}\)（\(x_i \in \{0, 1\}\)，\(\overline{x_i}\) 为 \(x_i\) 取反后的结果，\(E\) 是给定的组合）。
此时，我们考虑用最小割建模，由于网络的一组割一定会把 \(s\) 和 \(t\) 之间的所有路径都去掉一条边，那么我们从 \(s\) 往 \(u\) 连一条边权为 \(a_u\) 的边，从 \(u\) 往 \(t\) 连一条边权为 \(b_u\) 的边，此时我们构建出了一条从 \(s\) 到 \(t\) 的路径，我们必须割掉任意一条边，此时就会将对应的权值加入答案。
对于 \(w_{u, v}\)，我们在 \(u\) 和 \(v\) 之间连一条边权为 \(w_{u, v}\) 的双向边，此时，若 \(u, v\) 不属于同一个集合，那么 \((u, v)\) 和 \((v, u)\) 中至少割掉了一条边。如果割掉了 \((u, v)\) 这条边，那么 \(u\) 就和 \(s\) 联通，而 \(v\) 和 \(t\) 联通，此时相当于把 \(u\) 放到了 \(A\) 集合，\(v\) 放到了 \(B\) 集合；如果割掉了 \((v, u)\) 这条边，那么就相当于把 \(u\) 放到了 \(A\) 集合，\(v\) 放到了 \(B\) 集合，满足了所有限制。
现在，还有几种情况没有处理：
-
\(a_i\) 和 \(b_i\) 有可能会出现负数，此时边的容量可能会出现负数的情况，无法跑最大流，此时我们需要给每条边加上一个容量使得容量非负，然后再减去增加量乘以最小割的边数即可。
-
\(c_{i, j}\) 有可能会出现负数，此时如果 \(c_{i, j}\) 全部为负，那么就将 \(c\) 全部取反，在最终结果中减去割掉的这些边的权值就可以了。如果 \(c_{i, j}\) 部分为负，那么这道题就不可以做了（虽然我不知道为什么）。
此时，我们跑一遍最大流，用总权值减掉最大流就可以得到答案了。
最大权闭合子图
一张有向图 \(G\) 的闭合子图 \(G'\) 满足对于所有点 \(u \in V'\)，\(u\) 的所有出边指向的点仍然属于 \(V'\)。而最大权闭合子图则是给每个点赋了一个权值 \(w_u\) 求所有闭合子图中点权和最大的那一个（可以发现最大权闭合子图不一定是极大的，因为有些点的点权为负）。
我们这样建模，我们先设出原点 \(s\) 和汇点 \(t\)，然后对于每个点权 \(w_u\) 大于 \(0\) 的点，我们从 \(s\) 往 \(u\) 连一条容量为 \(w_u\) 的边；对于每个点权 \(w_u\) 小于 \(0\) 的点，我们从 \(u\) 往 \(t\) 连一条容量为 \(-w_u\) 的边。最后，对于每条原图中的边，都把它的容量设成 \(\infty\)，则最大权闭合子图的值 \(=\) 原图中的正权和 \(-\) 新图的最大流。
我们考虑如何证明它的正确性。首先肯定需要把最大流转换成最小割。
设我们当前考虑到了闭合子图 \(G_1\)，它在 \(G\) 中的补集设为 \(G_2 = G - G_1\)，再设 \(V_1^+\) 为 \(G_1\) 中点权为正的点构成的点集，\(V_1^-\) 为 \(G_1\) 中点权为负的点构成的点集。同理定义 \(V_2^+\) 和 \(V_2^-\)。
此时我们确定下来了原图的一个划分，那么新图中的一个划分 \((S, T)\) 就是 \((s \cup V_1, t \cup V_2) = (V_1, V_2) \cup (V_1, t) \cup (s, V_2) \cup (s, t) = (s, V_2) \cup (t, V_1) = (s, V_2^+) \cup (V_1^-, t)\)，此时该划分对应的割的容量 \(c(S, T) = \displaystyle\sum_{u \in V_2^+} w_u + \sum_{u \in V_1^-} (-w_u)\)。
而最大权闭合子图的权值 \(w(V_1)\) 又被定义成 \(\displaystyle\sum_{u \in V_1^+} w_u + \sum_{u \in V_1^-} w_u = \sum_{u \in V_1^+} w_u - \sum_{u \in V_1^-} (-w_u)\)。将该式与上面的式子相加可以得到 \(w(V_1) + c(S, T) = \displaystyle\sum_{u \in V_2^+} w_u + \sum_{u \in V_1^-} (-w_u) + \sum_{u \in V_1^+} w_u - \sum_{u \in V_1^-} (-w_u) = \sum_{u \in V_2^+} w_u + \sum_{u \in V_1^+} w_u = \sum_{u \in V_1} w_u\)。
移项后，我们可以得到 \(w(V_1) = \displaystyle\sum_{u \in V_1} w_u - c(S, T)\)，由于图中正点权的和为定值，因此我们只需要求出最小割就可以了。
\(\text{DAG}\) 的最小不相交路径覆盖
这个问题需要我们用尽可能少的没有公共结点的路径去覆盖一个 \(\text{DAG}\)，使得每个点都被覆盖。
由于我们每个点只能经过一次，根据之前拆点 / 拆边模型的总结，我们将原图中的所有点拆成入点和出点，每个点的入点向出点连一条容量为 \(1\) 的边，这就限制了这条边只能走一次。而对于原图中的一条边 \((u, v)\)，我们从 \(u\) 的出点向 \(v\) 的入点连边，容量也为 \(1\)。
显然，我们一定可以用 \(n\) 条路径覆盖整张图，只是每条路径就相当于一个点。现在，由于所有入点和入点之间没有连边，出点和出点之间没有连边，因此这是一个二分图。我们跑一遍二分图的最大匹配，如果两个点 \(u, v\) 被匹配了，就相当于是把 \(u\) 处的路径与 \(v\) 处的路径合并在了一起，会使总路径数减少 \(1\)，因此我们用总点数减去二分图最大匹配数就可以求出答案。
关于用网络流求二分图最大匹配，参见网络流与线性规划 \(24\) 题中关于第 \(3\) 题的讲解。
\(\text{DAG}\) 的最小可相交路径覆盖
此时每个点可以经过多次，不是很好搞，那么我们考虑两条路径 \(u_1 \leadsto p \leadsto v_1\) 和 \(u_2 \leadsto p \leadsto v_2\)，此时我们不希望这两条路径相交，于是我们从 \(u_2\) 向 \(v_2\) 连一条边，这样第 \(2\) 条路径就不会经过 \(p\) 了。因此我们跑一遍传递闭包，把连通的两个点之间连一条边，这样就可以转化成最小不相交路径问题了。这相当于是对原图进行了如下操作：
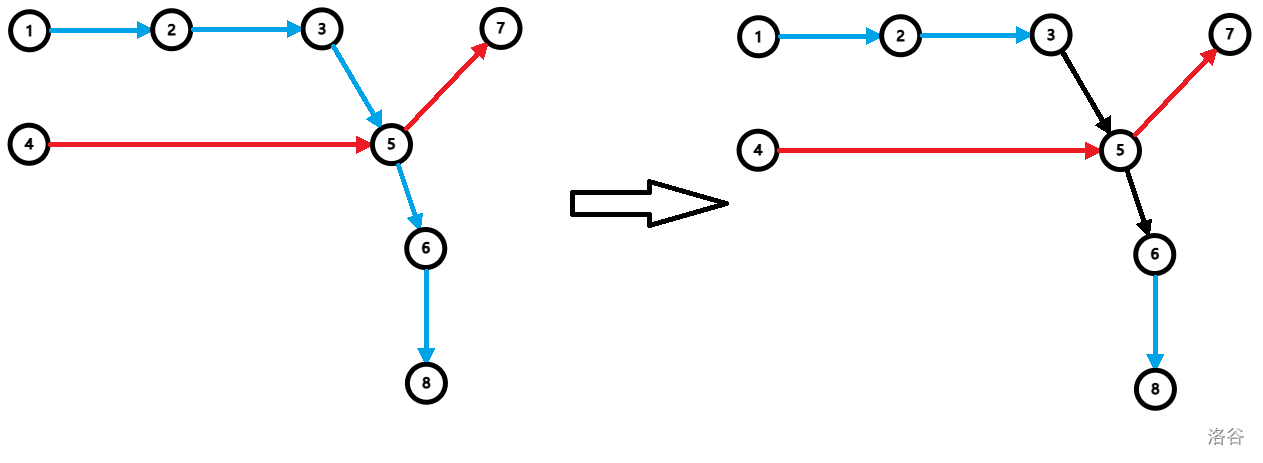
从图中也可以看出，此时一条路径上的点可以不直接相邻。
其实这就是 \(\text{Dilworth}\) 定理，偏序集的最长反链等于其最小不可重链覆盖。而在 \(\text{DAG}\) 中，每个点只会向编号比它大的点连边，这就是一种偏序关系。但是只告诉我们连边方式，这样的偏序集是不完整的，因此我们用传递闭包找到所有与 \(u\) 连通且编号比 \(u\) 大的点，此时偏序集就完整了，我们可以通过求出其最小不可重链覆盖来求出答案。
流量一定权值最大（小）模型
此模型用于解决流量一定时，所有增广路的某种性质和的最大值和最小值，详见P2770 航空路线问题的讲解。
流量守恒模型
此模型利用流量守恒求解了一些区间覆盖问题，详见P3358 最长k可重区间集问题的讲解。
网络流与线性规划 \(24\) 题
由于网络流的例题实在是太多了，因此接下来的代码中都只会放上建模部分的代码。
3.洛谷 P2756 飞行员配对方案问题
多倍经验：洛谷 P3386 【模板】二分图最大匹配、洛谷 B3605 [图论与代数结构 401] 二分图匹配
在这里我们来介绍一下如何用网络流求解二分图最大匹配。
我们考虑一个左部点最多只会与一个右部点连边，根据流量限制模型，我们从 \(s\) 向每个左部点连一条容量为 \(1\) 的边，从每右部点向 \(t\) 连一条容量为 \(1\) 的边。之前二分图中所有边的容量全部设成 \(1\)，此时从每个左部点出发只会有容量为 \(1\) 的流，到达每个右部点的流也只有 \(1\)，那么此时就完成了二分图的匹配。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e2 + 9, M = 2e4 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, s, t;
bool bfs();
int dfs(int u, int flow);
int ans;
signed main(){
scanf("%lld%lld", &m, &n);
s = n + 1, t = n + 2;
while(true){
int u, v;
scanf("%lld%lld", &u, &v);
if(u == -1 && v == -1)
break;
addEdge(u, v, 1);
addEdge(v, u, 0);
}
for(int i = 1; i <= m; i++){
addEdge(s, i, 1);
addEdge(i, s, 0);
}
for(int i = m + 1; i <= n; i++){
addEdge(i, t, 1);
addEdge(t, i, 0);
}
n += 2;
while(bfs())
ans += dfs(s, INF);
n -= 2;
printf("%lld\n", ans);
for(int u = 1; u <= m; u++){
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(v <= n && e[i ^ 1].c == 1){
printf("%lld %lld\n", u, v);
break;
}
}
}
return 0;
}
5.洛谷 P2762 太空飞行计划问题
多倍经验：洛谷 P3410 拍照
我们把每个实验和每个仪器抽象成点，把依赖关系抽象成边，此时做每个实验可以增加收益，买每个仪器会减少收益，那么这就变成了一个最大权闭合子图问题，直接做就完了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e2 + 9, M = 5e3 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, s, t;
bool bfs();
int dfs(int u, int flow);
int ans, sum;
signed main(){
scanf("%lld%lld", &m, &n);
s = m + n + 1, t = m + n + 2;
for(int i = 1; i <= m; i++){
int x;
scanf("%lld", &x);
addEdge(s, i, x);
addEdge(i, s, x);
sum += x;
while(getchar() == ' '){
scanf("%lld", &x);
addEdge(i, x + m, INF);
addEdge(x + m, i, 0);
}
}
for(int i = 1; i <= n; i++){
int x;
scanf("%lld", &x);
addEdge(i + m, t, x);
addEdge(t, i + m, x);
}
n += m + 2;
while(bfs())
ans += dfs(s, INF);
n -= m + 2;
for(int i = 1; i <= m; i++)
if(dep[i] != INF)
printf("%lld ", i);
printf("\n");
for(int i = 1; i <= n; i++)
if(dep[i + m] != INF)
printf("%lld ", i);
printf("\n");
printf("%lld", sum - ans);
return 0;
}
7.洛谷 P2764 最小路径覆盖问题
多倍经验：UVA1184 Air Raid
这就是 \(\text{DAG}\) 最小不想交路径覆盖的板子题，只是输出方案比较麻烦。我们先找到哪些出点和入点对只有出点往外有流，这就是一条链的开头，从这个点开始不断找流满的边，就可以找到一条路径了（注意你走到的全是入点，再往后 DFS 时需要跳到该入点对应的出点）。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 9, M = 1e5 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, s, t;
bool bfs();
int dfs(int u, int flow);
int vis[N], ans;
signed main(){
scanf("%lld%lld", &n, &m);
s = 2 * n + 1, t = 2 * n + 2;
for(int i = 1; i <= m; i++){
int u, v;
scanf("%lld%lld", &u, &v);
addEdge(u, v + n, 1);
addEdge(v + n, u, 0);
}
for(int i = 1; i <= n; i++){
addEdge(s, i, 1);
addEdge(i, s, 0);
}
for(int i = 1; i <= n; i++){
addEdge(i + n, t, 1);
addEdge(t, i + n, 0);
}
n = n * 2 + 2;
while(bfs())
ans += dfs(s, INF);
n = (n - 2) / 2;
for(int i = 1; i <= n; i++){
if(!vis[i]){
int tmp = i + n, beg = true;
for(int j = head[tmp]; j; j = e[j].nex){
int v = e[j].v;
if(v >= 1 && v <= n && e[j].c){
beg = false;
break;
}
}
if(!beg)
continue;
int u = i;
printf("%lld ", u);
while(true){
bool flag = false;
for(int j = head[u]; j; j = e[j].nex){
int v = e[j].v;
if(v > n && v <= 2 * n && !e[j].c){
flag = true;
printf("%lld ", v - n);
vis[v - n] = true;
u = v - n;
break;
}
}
if(!flag)
break;
}
printf("\n");
}
}
printf("%lld\n", n - ans);
return 0;
}
8.洛谷 P2765 魔术球问题
假设有 \(n\) 个数，每个数朝比它大且与它的和为平方数的数连边，跑一遍 \(\text{DAG}\) 的最小不相交路径覆盖就可以得到这 \(n\) 个数最少可以放在多少个柱子上。因此我们对 \(n\) 二分答案就可以了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 9, M = 1e5 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, s, t;
bool bfs(int lim);
int dfs(int u, int flow);
int vis[N], ans, res, tmp = 1;
signed main(){
scanf("%lld", &n);
int l = 1, r = 3000;
while(l <= r){
int mid = (l + r) >> 1;
memset(head, 0, sizeof(head));
ecnt = tmp = 1, ans = 0;
s = 2 * mid + 1, t = 2 * mid + 2;
for(int i = 1; i <= mid; i++){
while(tmp * tmp - i <= i)
tmp++;
for(int j = tmp; j * j - i <= mid; j++){
addEdge(i, j * j - i + mid, 1);
addEdge(j * j - i + mid, i, 0);
}
}
for(int i = 1; i <= mid; i++){
addEdge(s, i, 1);
addEdge(i, s, 0);
}
for(int i = 1; i <= mid; i++){
addEdge(i + mid, t, 1);
addEdge(t, i + mid, 0);
}
while(bfs(mid * 2 + 2))
ans += dfs(s, INF);
if(mid - ans <= n){
if(mid - ans == n)
res = mid;
l = mid + 1;
} else
r = mid - 1;
}
printf("%lld\n", res);
memset(head, 0, sizeof(head));
ecnt = tmp = 1, ans = 0;
s = 2 * res + 1, t = 2 * res + 2;
for(int i = 1; i <= res; i++){
while(tmp * tmp - i <= i)
tmp++;
for(int j = tmp; j * j - i <= res; j++){
addEdge(i, j * j - i + res, 1);
addEdge(j * j - i + res, i, 0);
}
}
for(int i = 1; i <= res; i++){
addEdge(s, i, 1);
addEdge(i, s, 0);
}
for(int i = 1; i <= res; i++){
addEdge(i + res, t, 1);
addEdge(t, i + res, 0);
}
while(bfs(res * 2 + 2))
ans += dfs(s, INF);
for(int i = 1; i <= res; i++){
if(!vis[i]){
int tmp = i + res, beg = true;
for(int j = head[tmp]; j; j = e[j].nex){
int v = e[j].v;
if(v >= 1 && v <= res && e[j].c){
beg = false;
break;
}
}
if(!beg)
continue;
int u = i;
printf("%lld ", u);
while(true){
bool flag = false;
for(int j = head[u]; j; j = e[j].nex){
int v = e[j].v;
if(v > res && v <= 2 * res && !e[j].c){
flag = true;
printf("%lld ", v - res);
vis[v - res] = true;
u = v - res;
break;
}
}
if(!flag)
break;
}
printf("\n");
}
}
return 0;
}
9.洛谷 P2766 最长不下降子序列问题
首先，我们跑一遍朴素的 DP，设 \(dp_i\) 表示以 \(i\) 结尾的最长不下降子序列长度，那么可以简单的写出 DP 转移方程 \(dp_i = \displaystyle\max_{j < i \wedge a_j \leq a_i} dp_j + 1\)，那么就求出第一问的答案，设答案为 \(ans\)。
因此，只有 \(dp_i = 1\) 的位置可以作为最长不下降子序列的开头，而只有 \(dp_i = ans\) 的位置可以作为最长不下降子序列的结尾。那么我们可以建立出超级源点和超级汇点，从超级汇点往每个 \(dp_i = 1\) 的位置连边，表示这个点可以作为起点；从 \(dp_i = ans\) 的位置往超级汇点连边，表示这个点可以作为终点。再对于每个 \(j < i \wedge a_j \leq a_i\)，从 \(j\) 往 \(i\) 连一条边，表示 \(i\) 可以拼在 \(j\) 后面。这三类边容量全部为 \(\infty\)。
最后，有些元素会有使用次数限制，那么直接根据拆点模型，把一个点拆成入点和出点，中间连容量为使用次数的边即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e3 + 9, M = 1e5 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, s, t;
bool bfs();
int dfs(int u, int flow);
int f[N], a[N], maxn, ans;
signed main(){
scanf("%lld", &n);
if(n == 1){
printf("1\n1\n1");
return 0;
}
s = 2 * n + 1, t = 2 * n + 2;
for(int i = 1; i <= n; i++)
scanf("%lld", &a[i]);
for(int i = 1; i <= n; i++){
f[i] = 1;
for(int j = i - 1; j >= 1; j--)
if(f[j] + 1 > f[i] && a[i] >= a[j])
f[i] = f[j] + 1;
for(int j = i - 1; j >= 1; j--)
if(f[j] + 1 == f[i] && a[i] >= a[j]){
addEdge(j, i + n, 1);
addEdge(i + n, j, 0);
}
maxn = max(maxn, f[i]);
}
printf("%lld\n", maxn);
for(int i = 1; i <= n; i++){
if(f[i] == 1){
addEdge(s, i + n, 1);
addEdge(i + n, s, 0);
}
if(f[i] == maxn){
addEdge(i, t, 1);
addEdge(t, i, 0);
}
addEdge(i + n, i, 1);
addEdge(i, i + n, 0);
}
n = 2 * n + 2;
while(bfs())
ans += dfs(s, INF);
n = (n - 2) / 2;
printf("%lld\n", ans);
memset(head, 0, sizeof(head));
ecnt = 1;
for(int i = 1; i <= n; i++){
for(int j = i - 1; j >= 1; j--)
if(f[j] + 1 == f[i] && a[i] >= a[j]){
addEdge(j, i + n, 1);
addEdge(i + n, j, 0);
}
maxn = max(maxn, f[i]);
}
for(int i = 1; i <= n; i++){
if(f[i] == 1){
addEdge(s, i + n, 1);
addEdge(i + n, s, 0);
}
if(f[i] == maxn){
addEdge(i, t, 1);
addEdge(t, i, 0);
}
addEdge(i + n, i, 1);
addEdge(i, i + n, 0);
}
addEdge(s, 1 + n, INF);
addEdge(1 + n, s, 0);
addEdge(1 + n, 1, INF);
addEdge(1, 1 + n, 0);
if(f[n] == maxn){
addEdge(n, t, INF);
addEdge(t, n, 0);
addEdge(n + n, n, INF);
addEdge(n, n + n, 0);
}
n = 2 * n + 2, ans = 0;
while(bfs())
ans += dfs(s, INF);
n = (n - 2) / 2;
printf("%lld\n", ans);
return 0;
}
10.洛谷 P2770 航空路线问题
容易发现航线方向并没有影响，我们只需要找出两条从 \(1\) 到 \(n\) 的航线，并且要途径的城市最多。这看起来就像是找到两条增广路，使得路径长度和最大。由于找增广路只能保证增加的流量最大，而这道题流量已经定下来了，为 \(2\)，因此无法通过朴素最大流得到答案，考虑费用流。其实，对于这种流量一定，最大（小）化所有增广路的某种边权和的题，我们都可以考虑费用流。
我们可以观察到，除了 \(1\) 和 \(n\)，其它每个点只能经过一次，因此考虑拆点，从入点向出点连一条容量为 \(1\)，费用为 \(1\) 的边，表示这个城市只能经过一次，会使得途径的城市增加 \(1\)。对于 \(1\) 和 \(n\) 号点，只用将容量改为 \(2\) 就可以了。
最后，由于点不会重复，因此路径上的边极大概率不会重复，除了直接连接 \(u\) 和 \(v\) 的边。此时，就把这种边的容量设为 \(2\)，其它边容量设为 \(1\) 就可以了。
关于输出方案的部分，可以从 \(1\) 号点开始做两次 DFS，根据反向边得流量判断这条边还能不能走，DFS 完后把这条 \(1\) 到 \(n\) 路径上的边的反向边容量都减去 \(1\) 就可以了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 1e5 + 9, M = 1e5 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, w, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int w){
e[++ecnt] = Edge{v, c, w, head[u]};
head[u] = ecnt;
}
int cur[N], dis[N], n, m, s, t;
queue <int> q;
bool inq[N];
bool spfa();
bool vis[N];
pii dfs(int u, int flow);
int flg[N], ans, res;
map <int, string> name;
map <string, int> id;
string ch, ch2;
vector <string> vec;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
s = n + 1, t = n;
for(int i = 1; i <= n; i++){
cin >> ch;
id[ch] = i;
name[i] = ch;
}
for(int i = 1; i <= m; i++){
cin >> ch >> ch2;
int u = id[ch], v = id[ch2];
if(u > v)
swap(u, v);
if(u == 1 && v == n){
addEdge(u, v + n, 2, 0);
addEdge(v + n, u, 0, 0);
} else {
addEdge(u, v + n, 1, 0);
addEdge(v + n, u, 0, 0);
}
}
for(int i = 1; i <= n; i++){
if(i == n || i == 1){
addEdge(i + n, i, 2, -1);
addEdge(i, i + n, 0, 1);
} else {
addEdge(i + n, i, 1, -1);
addEdge(i, i + n, 0, 1);
}
}
n = n * 2;
while(spfa()){
pii tmp = dfs(s, INF);
ans += tmp.first;
res += tmp.second;
}
n /= 2;
if(ans == 2){
cout << -res - 2 << endl;
int u = 1;
cout << name[1] << endl;
while(true){
bool flag = false;
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(e[i ^ 1].c && !flg[v - n]){
cout << name[v - n] << endl;
u = v - n;
if(u == n)
flag = true;
else
flg[u] = true;
break;
}
}
if(flag)
break;
}
u = 1;
while(true){
bool flag = false;
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(e[i ^ 1].c && !flg[v - n]){
u = v - n;
if(u == n)
flag = true;
else {
vec.push_back(name[v - n]);
flg[u] = true;
}
break;
}
}
if(flag)
break;
}
for(int i = vec.size() - 1; i >= 0; i--)
cout << vec[i] << endl;
cout << name[1];
} else
printf("No Solution!");
return 0;
}
11.洛谷 P2774 方格取数问题
多倍经验：洛谷 P4474 王者之剑
考虑到一个格子中的数选了后，它上下左右的数都不能选了，这看起来很像最小割模型，我们考虑怎么建模。
由于最小割模型考虑的是两个集合，那么我们考虑如何将这张图划分成两个部分。首先处在对角线上的两个数字肯定能同时选，因此我们将这张棋盘黑白染色，横纵坐标之和为偶数的格子染成黑色，横纵坐标之和为奇数的格子染成白色，那么原图就变成一个二分图，比较像最小割模型的样子了。
其实，之前讲的最小割模型还有一种建图方式，那就是将一个点拆成入点和出点，中间连容量为 \(\infty\) 的边，那么这条边在最小割时一定不会被割掉，割掉的还是容量为 \(a_u\) 或 \(b_u\) 的两条边（虽然这似乎很无用）。但这种建模方式对这道题比较有启发，因为选一个点，损失的是别人的权值。因此每个点向与它相邻的点连边，容量为 \(\infty\)，我们再建立超级汇点向所有左部点连边，从所有右部点向超级汇点连边，容量为这个点的权值。
我们现在考虑每一个左部点，它连了一个这样的子图：
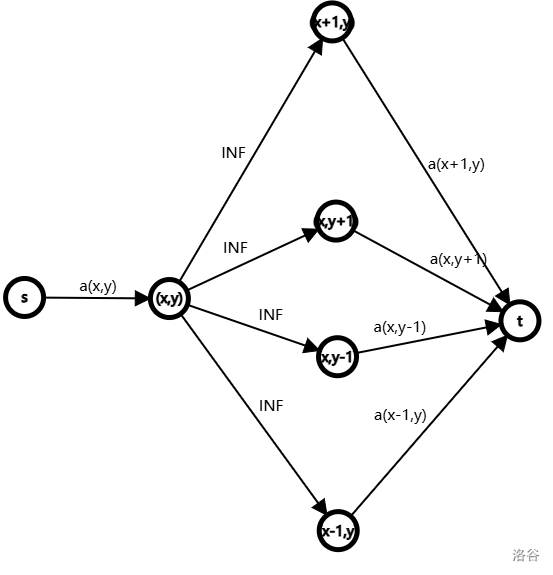
由于求最小割，因此容量为 \(\infty\) 的边一定不会被割掉。但是由于要让 \(s\) 和 \(t\) 不连通，那么要么割掉容量为 \(a_{x, y}\) 的边，要么割掉容量为 \(a_{x + 1, y}, a_{x, y + 1}, a_{x, y - 1}, a_{x - 1, y}\) 的这 \(4\) 条边，满足了题目选择格子不能相邻的要求，那么这道题就做完了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e4 + 9, M = 1e5 + 9, K = 1e2 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, s, t;
bool bfs();
int dfs(int u, int flow);
int c[K][K], d[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}, ans, sum;
signed main(){
scanf("%lld%lld", &m, &n);
s = m * n + 1, t = m * n + 2;
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++){
scanf("%lld", &c[i][j]);
sum += c[i][j];
}
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if((i + j) & 1){
addEdge(s, (i - 1) * n + j, c[i][j]);
addEdge((i - 1) * n + j, s, 0);
} else {
addEdge((i - 1) * n + j, t, c[i][j]);
addEdge(t, (i - 1) * n + j, 0);
}
}
}
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++){
if(!((i + j) & 1))
continue;
for(int k = 0; k < 4; k++){
int dx = i + d[k][0];
int dy = j + d[k][1];
if(dx < 1 || dx > m || dy < 1 || dy > n)
continue;
addEdge((i - 1) * n + j, (dx - 1) * n + dy, INF);
addEdge((dx - 1) * n + dy, (i - 1) * n + j, 0);
}
}
n = m * n + 2;
while(bfs())
ans += dfs(s, INF);
printf("%lld\n", sum - ans);
return 0;
}
13.洛谷 P3254 圆桌问题
这就是很典型的限制流量模型，我们从源点向每个单位连一条容量为 \(r_i\) 的边，从每个桌子向汇点连一条容量为 \(c_i\) 的边，每个单位再向每个桌子连一条容量为 \(1\) 的边。
跑完最大流后，如果有一条容量为 \(r_i\) 的边没有流满，证明有 \(1\) 个单位中有代表无法被安排座位，此时不存在方案。如果存在方案，那么我们就看一个单位连出去的所有边中，哪些边流满了，此时这个单位就往这些边所指的桌子派了一个代表。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e3 + 9, M = 4e4 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, s, t;
bool bfs();
int dfs(int u, int flow);
int r[N], c[N], ans;
signed main(){
scanf("%lld%lld", &m, &n);
s = m + n + 1, t = m + n + 2;
for(int i = 1; i <= m; i++){
scanf("%lld", &r[i]);
addEdge(s, i, r[i]);
addEdge(i, s, 0);
}
for(int i = 1; i <= n; i++){
scanf("%lld", &c[i]);
addEdge(i + m, t, c[i]);
addEdge(t, i + m, 0);
}
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++){
addEdge(i, j + m, 1);
addEdge(j + m, i, 0);
}
n += m + 2;
while(bfs())
ans += dfs(s, INF);
n -= m + 2;
bool flag = true;
for(int u = 1; u <= m; u++){
int cnt = 0;
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(v <= n + m && e[i ^ 1].c)
cnt++;
}
if(cnt != r[u]){
flag = false;
break;
}
}
printf("%d\n", flag);
if(flag){
for(int u = 1; u <= m; u++){
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(v <= n + m && e[i ^ 1].c)
printf("%lld ", v - m);
}
printf("\n");
}
}
return 0;
}
14.洛谷 P3355 骑士共存问题
多倍经验：洛谷 P4304 [TJOI2013] 攻击装置、洛谷 P5030 长脖子鹿放置
这依然是最小割模型。
由于骑士只能攻击异色格，那么这个棋盘依然可以黑白染色，那么就按照洛谷 P2774 方格取数问题的做法去做就行了。
不过有些时候，比如洛谷 P5030 长脖子鹿放置这道题，长脖子鹿可以攻击到同色格，此时我们就不能向洛谷 P2774 方格取数问题这样黑白染色了。不过我们观察到，相间的两行一定不会互相攻击，因此我们把横坐标为奇数染成黑色，横坐标为偶数的染成白色，然后就和洛谷 P2774 方格取数问题一样了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 4e4 + 9, M = 4e5 + 9, K = 2e2 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, s, t;
bool bfs();
int dfs(int u, int flow);
int flag[K][K], d[8][2] = {{-1, -2}, {-2, -1}, {-2, 1}, {-1, 2}, {1, -2}, {2, -1}, {2, 1}, {1, 2}}, ans;
signed main(){
scanf("%lld%lld", &n, &m);
s = n * n + 1, t = n * n + 2;
for(int i = 1; i <= m; i++){
int x, y;
scanf("%lld%lld", &x, &y);
flag[x][y] = 1;
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
if(flag[i][j])
continue;
if((i + j) & 1){
addEdge(s, (i - 1) * n + j, 1);
addEdge((i - 1) * n + j, s, 0);
} else {
addEdge((i - 1) * n + j, t, 1);
addEdge(t, (i - 1) * n + j, 0);
}
}
}
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++){
if(flag[i][j] || !((i + j) & 1))
continue;
for(int k = 0; k < 8; k++){
int dx = i + d[k][0];
int dy = j + d[k][1];
if(dx < 1 || dx > n || dy < 1 || dy > n || flag[dx][dy])
continue;
addEdge((i - 1) * n + j, (dx - 1) * n + dy, INF);
addEdge((dx - 1) * n + dy, (i - 1) * n + j, 0);
}
}
n = n * n + 2;
while(bfs())
ans += dfs(s, INF);
n -= 2;
printf("%lld\n", n - m - ans);
return 0;
}
15.洛谷 P3356 火星探险问题
终于遇到一道需要拆边的题目了。
首先，每个点可以经过多次，但是贡献只算一次，因此我们考虑拆点，从每个石块入点向出点先连一条容量为 \(1\) 的，费用为 \(1\) 的边，再连一条容量为 \(\infty\)，费用为 \(0\) 的边，此时就限定了贡献只能算一次。输出方案就和洛谷 P2770 航空路线问题一样了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 5e3 + 9, M = 5e4 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, w, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int w){
e[++ecnt] = Edge{v, c, w, head[u]};
head[u] = ecnt;
}
int cur[N], dis[N], n, m, s, t;
bool inq[N];
bool spfa();
bool vis[N];
pii dfs(int u, int flow);
int id[N][N], ans, res, a, b, p, q, tot;
bool flag[N];
void getans(int now, int u){
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;//入点
v -= p * q;
if(v >= 0 && v <= p * q && e[i ^ 1].c){
e[i ^ 1].c--;
if(v == u + 1)
printf("%lld 1\n", now);
else
printf("%lld 0\n", now);
if(v == p * q)
return;
getans(now, v);
break;
}
}
}
signed main(){
scanf("%lld%lld%lld", &a, &p, &q);
n = p * q;
for(int i = 1; i <= q; i++)
for(int j = 1; j <= p; j++)
id[i][j] = ++tot;
s = n * 2 + 1, t = n * 2;
addEdge(s, 1, a, 0);
addEdge(1, s, 0, 0);
for(int i = 1; i <= q; i++)
for(int j = 1; j <= p; j++){
int c;
scanf("%lld", &c);
if(c == 0){
addEdge(id[i][j] + n, id[i][j], INF, 0);
addEdge(id[i][j], id[i][j] + n, 0, 0);
} else if(c == 1){
addEdge(id[i][j] + n, id[i][j], 0, 0);
addEdge(id[i][j], id[i][j] + n, 0, 0);
} else {
addEdge(id[i][j] + n, id[i][j], 1, -1);
addEdge(id[i][j], id[i][j] + n, 0, 1);
addEdge(id[i][j] + n, id[i][j], INF, 0);
addEdge(id[i][j], id[i][j] + n, 0, 0);
}
if(id[i][j + 1]){
addEdge(id[i][j], id[i][j + 1] + n, INF, 0);
addEdge(id[i][j + 1] + n, id[i][j], 0, 0);
}
if(id[i + 1][j]){
addEdge(id[i][j], id[i + 1][j] + n, INF, 0);
addEdge(id[i + 1][j] + n, id[i][j], 0, 0);
}
}
n = n * 2 + 1;
while(spfa()){
pii tmp = dfs(s, INF);
ans += tmp.first;
res += tmp.second;
}
n = (n - 1) / 2;
for(int i = 1; i <= ans; i++)
getans(i, 1);//从 i 的出点开始
return 0;
}
17.洛谷 P3358 最长k可重区间集问题
不相交的区间是不会对一个点的区间数造成更多贡献的，因此问题变成选出 \(k\) 组区间集，每个集合内的区间互不相交且这 \(k\) 组权值之和最大。
首先，这道题又是限制了流量，求路径某种性质的最大值，因此考虑最大费用最大流。我们将区间编号。由于每个区间 \([l_i, r_i]\) （注意题目中是开区间）只能选一次，因此我们从 \(l_i\) 向 \(r_i\) 连一条容量为 \(1\)（由于这是区间，我们已经有入点 \(l_i\) 和出点 \(r_i\) 了，不需要拆点），费用为 \(r_i - l_i\) 的边。由于每次选出的区间集中每个区间都不能相交，因此我们对于所有 \(l_j \geq r_i\)，都从第 \(i\) 个区间向第 \(j\) 个区间连一条容量为 \(1\)，费用为 \(0\) 的边。此时跑一边最大费用最大流即可得出答案，但是边数是 \(O(n^2)\) 的，肯定会炸，考虑如何优化。
其实，我们大部分的边都用于连接两个不相交的区间了，根据 CF1956F Nene and the Passing Game 的想法，我们从坐标轴上每个点向它的下一个点连一条容量为 \(k\)，费用为 \(0\) 的边，对于每个区间 \([l_i, r_i]\)，我们依然从 \(l_i\) 向 \(r_i\) 连一条容量为 \(1\)，费用为 \(r_i - l_i\) 的边，此时保证了整个网络中的流等于 \(k\)，因此所有横跨坐标轴上一个点 \(u\) 的所有边 \([l_i, r_i]\) 中，流满的边不会超过 \(k\) 条，满足了题目要求。此时，我们图中的边数就从 \(O(n^2)\) 降到了 \(O(n)\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 5e3 + 9, M = 5e4 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, w, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int w){
e[++ecnt] = Edge{v, c, w, head[u]};
head[u] = ecnt;
}
int cur[N], dis[N], n, m, k, s, t;
queue <int> q;
bool inq[N];
bool spfa();
bool vis[N];
pii dfs(int u, int flow);
int l[N], r[N], tmp[N], ans, res, tot;
signed main(){
scanf("%lld%lld", &n, &k);
for(int i = 1; i <= n; i++){
scanf("%lld%lld", &l[i], &r[i]);
tmp[++tot] = l[i], tmp[++tot] = r[i];
}
sort(tmp + 1, tmp + tot + 1);
tot = unique(tmp + 1, tmp + tot + 1) - (tmp + 1);
for(int i = 1; i <= n; i++){
l[i] = lower_bound(tmp + 1, tmp + tot + 1, l[i]) - tmp;
r[i] = lower_bound(tmp + 1, tmp + tot + 1, r[i]) - tmp;
addEdge(l[i], r[i], 1, -(tmp[r[i]] - tmp[l[i]]));
addEdge(r[i], l[i], 0, (tmp[r[i]] - tmp[l[i]]));
}
for (int i = 0; i < tot; i++){
addEdge(i, i + 1, k, 0);
addEdge(i + 1, i, 0, 0);
}
s = 0, n = t = tot;
while(spfa()){
pii tmp = dfs(s, INF);
res += tmp.second;
}
printf("%lld", -res);
return 0;
}
20.洛谷 P4012 深海机器人问题
和洛谷 P3356 火星探险问题问题一样，只不过权值在边上，甚至都不用拆点了，直接在两个相邻格子之间连两条重边即可。注意到这道题目有多源点和汇点，需要用限制流量模型。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 5e3 + 9, M = 5e4 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, w, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int w){
e[++ecnt] = Edge{v, c, w, head[u]};
head[u] = ecnt;
}
int cur[N], dis[N], n, m, s, t;
bool inq[N];
bool spfa();
bool vis[N];
pii dfs(int u, int flow);
int id[N][N], ans, res, a, b, p, q, tot;
signed main(){
scanf("%lld%lld%lld%lld", &a, &b, &p, &q);
s = (p + 1) * (q + 1) + 1, n = t = (p + 1) * (q + 1) + 2;
for(int i = 0; i <= p; i++)
for(int j = 0; j <= q; j++)
id[i][j] = ++tot;
for(int i = 0; i <= p; i++)
for(int j = 0; j < q; j++){
int c;
scanf("%lld", &c);
addEdge(id[i][j], id[i][j + 1], INF, 0);
addEdge(id[i][j + 1], id[i][j], 0, 0);
addEdge(id[i][j], id[i][j + 1], 1, -c);
addEdge(id[i][j + 1], id[i][j], 0, c);
}
for(int j = 0; j <= q; j++)
for(int i = 0; i < p; i++){
int c;
scanf("%lld", &c);
addEdge(id[i][j], id[i + 1][j], INF, 0);
addEdge(id[i + 1][j], id[i][j], 0, 0);
addEdge(id[i][j], id[i + 1][j], 1, -c);
addEdge(id[i + 1][j], id[i][j], 0, c);
}
for(int i = 1; i <= a; i++){
int k, x, y;
scanf("%lld%lld%lld", &k, &x, &y);
addEdge(s, id[x][y], k, 0);
addEdge(id[x][y], s, 0, 0);
}
for(int i = 1; i <= b; i++){
int r, x, y;
scanf("%lld%lld%lld", &r, &x, &y);
addEdge(id[x][y], t, r, 0);
addEdge(t, id[x][y], 0, 0);
}
while(spfa()){
pii tmp = dfs(s, INF);
res += tmp.second;
}
printf("%lld", -res);
return 0;
}
21.洛谷 P4013 数字梯形问题
又是一道限制流量，求路径某种性质最大值的题目，依然考虑最大费用最大流。由于每个点都有经过次数的限制，而且权值在点上，因此直接套用拆点模型，从入点向出点连一条容量为使用次数，费用为点权的边。由于第一排每个点都是源点，于是最后再套用流量限制模型即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 5e3 + 9, M = 5e4 + 9, INF = 1e18 + 9;
int tot, n, m, s, t;
struct MCMF{
struct Edge{
int v, c, w, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int w){
e[++ecnt] = Edge{v, c, w, head[u]};
head[u] = ecnt;
}
int cur[N], dis[N];
queue <int> q;
bool inq[N];
bool spfa();
bool vis[N];
pii dfs(int u, int flow);
} g1, g2, g3;
int id[N][N], c[N][N], ans, res, cnt;
signed main(){
scanf("%lld%lld", &m, &n);
cnt = (m + m + n - 1) * n / 2;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m + i - 1; j++){
scanf("%lld", &c[i][j]);
id[i][j] = ++tot;
g1.addEdge(id[i][j] + cnt, id[i][j], 1, -c[i][j]);
g1.addEdge(id[i][j], id[i][j] + cnt, 0, c[i][j]);
g2.addEdge(id[i][j] + cnt, id[i][j], INF, -c[i][j]);
g2.addEdge(id[i][j], id[i][j] + cnt, 0, c[i][j]);
g3.addEdge(id[i][j] + cnt, id[i][j], INF, -c[i][j]);
g3.addEdge(id[i][j], id[i][j] + cnt, 0, c[i][j]);
}
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m + i - 1; j++){
if(id[i + 1][j]){
g1.addEdge(id[i][j], id[i + 1][j] + cnt, 1, 0);
g1.addEdge(id[i + 1][j] + cnt, id[i][j], 0, 0);
g2.addEdge(id[i][j], id[i + 1][j] + cnt, 1, 0);
g2.addEdge(id[i + 1][j] + cnt, id[i][j], 0, 0);
g3.addEdge(id[i][j], id[i + 1][j] + cnt, INF, 0);
g3.addEdge(id[i + 1][j] + cnt, id[i][j], 0, 0);
}
if(id[i + 1][j + 1]){
g1.addEdge(id[i][j], id[i + 1][j + 1] + cnt, 1, 0);
g1.addEdge(id[i + 1][j + 1] + cnt, id[i][j], 0, 0);
g2.addEdge(id[i][j], id[i + 1][j + 1] + cnt, 1, 0);
g2.addEdge(id[i + 1][j + 1] + cnt, id[i][j], 0, 0);
g3.addEdge(id[i][j], id[i + 1][j + 1] + cnt, INF, 0);
g3.addEdge(id[i + 1][j + 1] + cnt, id[i][j], 0, 0);
}
}
s = tot * 2 + 1, t = tot * 2 + 2;
for(int i = 1; i <= m; i++){
g1.addEdge(s, i + cnt, 1, 0);
g1.addEdge(i + cnt, s, 0, 0);
g2.addEdge(s, i + cnt, 1, 0);
g2.addEdge(i + cnt, s, 0, 0);
g3.addEdge(s, i + cnt, 1, 0);
g3.addEdge(i + cnt, s, 0, 0);
}
for(int i = 1; i <= m + n - 1; i++){
g1.addEdge(id[n][i], t, 1, 0);
g1.addEdge(t, id[n][i], 0, 0);
g2.addEdge(id[n][i], t, INF, 0);
g2.addEdge(t, id[n][i], 0, 0);
g3.addEdge(id[n][i], t, INF, 0);
g3.addEdge(t, id[n][i], 0, 0);
}
while(g1.spfa()){
pii tmp = g1.dfs(s, INF);
res += tmp.second;
}
printf("%lld\n", -res);
res = 0;
while(g2.spfa()){
pii tmp = g2.dfs(s, INF);
res += tmp.second;
}
printf("%lld\n", -res);
res = 0;
while(g3.spfa()){
pii tmp = g3.dfs(s, INF);
res += tmp.second;
}
printf("%lld", -res);
return 0;
}
23.洛谷 P4015 运输问题
流量限制模板题。限制完流量后，从每个仓库 \(i\) 向每个商店 \(j\) 连一条容量为 \(\infty\)，费用为 \(c_{i, j}\) 的边，跑最小费用最大流即可即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 2e2 + 9, M = 2e4 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, w, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int w){
e[++ecnt] = Edge{v, c, w, head[u]};
head[u] = ecnt;
}
int cur[N], dis[N], n, m, s, t;
queue <int> q;
bool inq[N];
bool spfa();
bool vis[N];
pii dfs(int u, int flow);
int a[N], b[N], c[N][N], res;
signed main(){
scanf("%lld%lld", &m, &n);
s = n + m + 1, t = n + m + 2;
for(int i = 1; i <= m; i++){
scanf("%lld", &a[i]);
addEdge(s, i, a[i], 0);
addEdge(i, s, 0, 0);
}
for(int i = 1; i <= n; i++){
scanf("%lld", &b[i]);
addEdge(i + m, t, b[i], 0);
addEdge(t, i + m, 0, 0);
}
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++){
scanf("%lld", &c[i][j]);
addEdge(i, j + m, INF, c[i][j]);
addEdge(j + m, i, 0, -c[i][j]);
}
n += m + 2;
while(spfa()){
pii tmp = dfs(s, INF);
res += tmp.second;
}
printf("%lld\n", res);
memset(head, 0, sizeof(head));
ecnt = 1;
res = 0;
n -= m + 2;
for(int i = 1; i <= m; i++){
addEdge(s, i, a[i], 0);
addEdge(i, s, 0, 0);
}
for(int i = 1; i <= n; i++){
addEdge(i + m, t, b[i], 0);
addEdge(t, i + m, 0, 0);
}
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++){
addEdge(i, j + m, INF, -c[i][j]);
addEdge(j + m, i, 0, c[i][j]);
}
n += m + 2;
while(spfa()){
pii tmp = dfs(s, INF);
res += tmp.second;
}
printf("%lld", -res);
return 0;
}
24.洛谷 P4016 负载平衡问题
多倍经验：洛谷 P2512 [HAOI2008] 糖果传递、洛谷 P5817 [CQOI2011] 分金币、UVA11300 Spreading the Wealth、洛谷 P2125 图书馆书架上的书
有网络流和贪心两种做法，但是所有多倍经验题都只能用贪心，因此最好还是写贪心吧。不过这道题能用贪心，相当于跑网络流时没有进行退流操作。
首先我们算出 \(a_i\) 的平均值 \(\overline a\)。如果 \(a_i < \overline a\)，那么它需要 \(\overline a − a_i\) 的货物；反之，它需要送出 \(a_i − \overline a\) 的货物。这又是一个流量限制模型。
不过我们需要最小化搬运量，因此还需要在设计网络时考虑给边加上费用。对于每个 \(i\)，向 \(i − 1\) 和 \(i + 1\)（如果超出范围则为 \(n\) 或 \(1\)）连边，容量为 \(\infty\)，费用为 \(1\)，因为货物可以随意移动。最后，跑最小费用最大流即可得出答案。
不过这显然无法处理 \(n \leq 10^6\) 的数据，因此我们考虑贪心。
设 \(x_i\) 表示 \(i\) 向 \(i\) 左侧的点送了多少货物（正数表示送出，负数表示接受）。记 \(nex\)
表示 \(i\) 右侧的点，那么有 \(\forall 1 \leq i \leq n, a_i + x_{nex} − x_i = \overline a\)。
我们把所有方程列成一个方程组：
从第 \(1\) 个式子中，我们可以得到 \(x_2\) 与 \(x_1\) 的关系；把前两个式子加起来可以得到 \(x_3\) 与 \(x_1\) 的关系；把前 \(3\) 个式子加起来可以得到 \(x_4\) 与 \(x_1\) 的关系……一般的，如果记 \(s_i = \displaystyle\sum_{j = 1}^{i - 1} \overline a - a_i\)，那么答案就为 \(\displaystyle\sum_{i = 1}^n |x_i| = \sum_{i = 1}^n |x_1 + s_i|\)，这相当于求数轴上的一个点到所有 \(-s_i\) 的距离之和最小，也就是到所有 \(s_i\) 的距离之和最小，那么 \(x_1\) 取 \(s_i\) 的中位数时，就可以取到最小值，因此我们花 \(O(n \log n)\) 的复杂度就解决了问题。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6 + 9;
int s[N], a[N], n, sum, ans;
signed main(){
scanf("%lld", &n);
for(int i = 1; i <= n; i++){
scanf("%lld", &a[i]);
sum += a[i];
}
sum /= n;
for(int i = 1; i <= n; i++)
s[i] = s[i - 1] + a[i] - sum;
sort(s + 1, s + n + 1);
for(int i = 1; i <= n; i++)
ans += abs(s[i] - s[n / 2 + 1]);
printf("%lld\n", ans);
return 0;
}
网络流建模杂题
我们现在已经会了一些基础的网络流建模方式了，现在开始就是一些比较考思维的题目了。
1.P2053 [SCOI2007] 修车
借用本题高赞题解的开头：
人不能两次踏进同一条河流。——赫拉克利
人不能两次踏进同一条河流，因为你第一次踏进的河流和第二次踏进的河流已经不是同一个河流了（水流走了）。同样地，对于一个修车工人而言，修第一辆车的他和修第二辆车的他不是同一个人。因为他已经让找他修车的其他人等待了一段时间。
如果一个工人 \(i\) 修的倒数第 \(j\) 辆车子是 \(k\)，那么这会对答案造成 \(\displaystyle\frac{jT_{k, i}}{n}\)。
那么我们考虑将一个工人拆成 \(n\) 个点 \((i, j)\)（\(j \in [1, n]\)），每个点表示修倒数第 \(j\) 辆车时的第 \(i\) 个工人，这样每个工人就只会修一辆车了。于是我们就从点 \((i, j)\) 向每一辆车 \(k\) 连一条容量为 \(1\)，费用为 \(jT_{k, i}\) 的边。最后建出源汇点之后跑最小费用最大流即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 5e3 + 9, M = 5e4 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, w, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int w){
e[++ecnt] = Edge{v, c, w, head[u]};
head[u] = ecnt;
}
int cur[N], dis[N], n, m, s, t;
queue <int> q;
bool inq[N];
bool spfa();
bool vis[N];
pii dfs(int u, int flow);
int ans, res;
signed main(){
scanf("%lld%lld", &m, &n);
s = (m + 1) * n + 1, t = (m + 1) * n + 2;
for(int i = 1; i <= n; i++){
addEdge(s, i, 1, 0);
addEdge(i, s, 0, 0);
}
for (int i = 1; i <= n * m; i++){
addEdge(i + n, t, 1, 0);
addEdge(t, i + n, 0, 0);
}
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++){
int x;
scanf("%lld", &x);
for(int k = 1; k <= n; k++){
addEdge(i, j * n + k, 1, x * k);
addEdge(j * n + k, i, 0, -x * k);
}
}
while(spfa()){
pii tmp = dfs(s, INF);
res += tmp.second;
}
printf("%.2lf", res * 1.0 / n);
return 0;
}
2.洛谷 P2050 [NOI2012] 美食节
这道题目是上一道题目的加强版，一个最朴素的想法就是如果将点了第 \(i\) 道菜的 \(p_i\) 个同学看成点的是不一样的菜，就和上一道题目一样了。但是这道题目 \(\displaystyle\sum p_i = p\) 已经是 \(800\) 了，比上一道题的 \(60\) 已经大了不少了，因此无法这么做。
我们仿照上一道题目建模，只不过这次我们从源点向每一道菜连一条容量为 \(p_i\)，费用为 \(0\) 的边。我们从每道菜向每个厨师 \((j, k)\) （注意 \(k \in [1, p]\)）连一条容量为 \(1\)，费用为 \(c_{i, j}k\) 的边，每个厨师再向汇点连一条容量为 \(1\)，费用为 \(0\) 的边，这时跑一次最小费用最大流即可。但是此时边的数量为 \(\mathcal O(mp + n)\) 的，点的数量是 \(\mathcal O(nmp)\) 的，只能得到 \(60\) 分，考虑优化。
其实我们发现会有大量浪费的节点，因为所有厨师总共只会做 \(n\) 道菜，最多只需要建出 \(n\) 个厨师节点。我们考虑这样一个事实，那就是只有当一个厨师做了倒数第 \(1\) 道菜，才可以做倒数第 \(2\) 道菜，以此类推。那么我们其实可以先把做最后一道菜的每个厨师建出来，然后跑一遍最小费用最大流，把到 \(t\) 的这条边流满了的厨师再建出新的点，以此类推，那么点数就降低到了 \(\mathcal O(n + m + p)\)，边数降低到了 \(\mathcal O(np)\)，可以通过此题了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 5e3 + 9, M = 5e4 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, w, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int w){
e[++ecnt] = Edge{v, c, w, head[u]};
head[u] = ecnt;
}
int cur[N], dis[N], n, m, s, t;
queue <int> q;
bool inq[N];
bool spfa();
int top[N];
bool vis[N], nxt[N];
pii dfs(int u, int flow);
int p[N], c[N][N], ans, res, sum;
signed main(){
scanf("%lld%lld", &n, &m);
for(int i = 1; i <= n; i++){
scanf("%lld", &p[i]);
sum += p[i];
}
s = m * sum + n + 1, t = m * sum + n + 2;
for(int i = 1; i <= n; i++){
addEdge(s, i, p[i], 0);
addEdge(i, s, 0, 0);
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
scanf("%lld", &c[i][j]);
addEdge(i, n + (j - 1) * sum + 1, 1, c[i][j]);
addEdge(n + (j - 1) * sum + 1, i, 0, -c[i][j]);
}
}
for(int i = 1; i <= m; i++){
top[i] = 1;
addEdge(n + (i - 1) * sum + 1, t, 1, 0);
addEdge(t, n + (i - 1) * sum + 1, 0, 0);
}
while(spfa()){
pii tmp = dfs(s, INF);
res += tmp.second;
for(int j = 1; j <= m; j++){
int now = n + (j - 1) * sum + top[j];
if(nxt[now] && top[j] < sum){
top[j]++;
for(int i = 1; i <= n; i++){
addEdge(i, now + 1, 1, c[i][j] * top[j]);
addEdge(now + 1, i, 0, -c[i][j] * top[j]);
}
addEdge(now + 1, t, 1, 0);
addEdge(t, now + 1, 0, 0);
}
}
}
printf("%lld", res);
return 0;
}
3.洛谷 P2469 [SDOI2010] 星际竞速
首先考虑普通的最小不相交路径覆盖，我们将一个点拆成入点和出点，从入点往出点连一条容量为 \(1\) 的边，不过由于有边权，因此必须跑最小费用最大流。这里有一个小的优化，如果 \(u\) 到 \(v\) 的边权大于 \(a_v\)，那么任何 \(u\) 到 \(v\) 的路径的边权和都大于 \(a_v\)，此时不如直接用能力爆发跳到 \(v\)，因此不用建出 \(u, v\) 这条边。
不过这道题麻烦在每一次重新开始一条路径还要花费一定代价，但中途经过这个点却不需要花费这一代价。我们依然从源点向每个入点连一条容量为 \(1\) 费用为 \(0\) 的边，从每个出点向汇点连一条容量为 \(1\) 费用为 \(0\) 的边，不过这时，我们再从源点向每个出点容量为 \(1\)，费用为 \(a_i\) 的边，这时如果一个点作为某条路径的开头，那么到它出点的所有边都没有被匹配，那么这时就多出来了一条 \(s \rightarrow out_u \rightarrow t\) 的增广路，由于要跑出最大流，那么这条增广路一定会流满，因此代价会加上 \(a_i\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 5e3 + 9, M = 5e4 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, w, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int w){
e[++ecnt] = Edge{v, c, w, head[u]};
head[u] = ecnt;
}
int cur[N], dis[N], n, m, s, t;
queue <int> q;
bool inq[N];
bool spfa();
bool vis[N];
pii dfs(int u, int flow);
int a[N], ans, res, sum;
signed main(){
scanf("%lld%lld", &n, &m);
s = n * 2 + 1, t = n * 2 + 2;
for(int i = 1; i <= n; i++){
scanf("%lld", &a[i]);
addEdge(s, i + n, 1, a[i]);
addEdge(i + n, s, 0, -a[i]);
addEdge(s, i, 1, 0);
addEdge(i, s, 0, 0);
addEdge(i + n, t, 1, 0);
addEdge(t, i + n, 0, 0);
}
for(int i = 1; i <= m; i++){
int u, v, w;
scanf("%lld%lld%lld", &u, &v, &w);
if(u > v)
swap(u, v);
if(w < a[v]){
addEdge(u, v + n, 1, w);
addEdge(v + n, u, 0, -w);
}
}
n = n * 2 + 2;
while(spfa()){
pii tmp = dfs(s, INF);
res += tmp.second;
}
printf("%lld", res);
return 0;
}
4.洛谷 P1361 小M的作物
多倍经验：洛谷 P1646 [国家集训队] happiness、洛谷 P4313 文理分科
这道题看起来就和最小割模型一模一样，不过此时两个作物种在一个田地里也会造成权值损失，因此我们考虑换一种方法简图，对于一对会造成贡献的一对作物 \(x_i, y_i\)，我们从源点向 \(x_i\) 连一条容量为 \(a_{x_i}\) 的边，从 \(x_i\) 向汇点连一条容量为 \(b_{x_i}\) 的边（\(y_i\) 同理），此时我们在新建一个节点 \(u\)，从源点向 \(u\) 连一条容量为 \(c_{1, i}\) 的边，再从 \(u\) 往 \(x_i\) 和 \(y_i\) 都连一条容量为 \(INF\) 的边（\(c_{2, i}\) 同理），此时我们考虑我们连出来的这张图的一个子图：
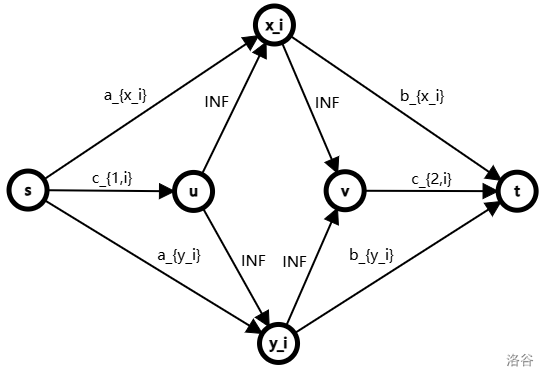
此时我们考虑 \(s \rightarrow x_i \rightarrow t\) 和 \(s \rightarrow y_i \rightarrow t\) 这两条路径，一共有四种不同割边方式：
-
如果割掉权值为 \(a_{x_i}\) 和 \(a_{y_i}\) 的这两条边，那么就没有割掉权值为 \(b_{x_i}\) 和 \(b_{y_i}\) 的这两条边，但是由于要在 \(s \rightarrow u \rightarrow x_i \rightarrow t\) 这条路径中割掉一条边，那么只能割掉 \(c_{1, i}\) 这条边。割掉权值为 \(b_{x_i}\) 和 \(b_{y_i}\) 的这两条边同理。
-
如果割掉权值为 \(a_{x_i}\) 和 \(b_{y_i}\) 的这两条边，那么就没有割掉权值为 \(b_{x_i}\) 和 \(a_{y_i}\) 的这两条边，但是由于要在 \(s \rightarrow u \rightarrow x_i \rightarrow t\) 和 \(s \rightarrow y_i \rightarrow v \rightarrow t\) 这两条路径中都割掉一条边，那么只能割掉 \(c_{1, i}\) 和 \(c_{2, i}\) 这条边。割掉权值为 \(a_{y_i}\) 和 \(b_{x_i}\) 的这两条边同理。
那么此时各种种植方式和割边的容量和就一致了，跑一边最大流即可得出答案。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 3e5 + 9, M = 1e6 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, s, t;
bool bfs();
int dfs(int u, int flow);
int ans, sum, tot;
signed main(){
scanf("%lld", &n);
s = N - 2, t = N - 1;
for(int i = 1; i <= n; i++){
int a;
scanf("%lld", &a);
addEdge(s, i, a);
addEdge(i, s, 0);
sum += a;
}
for(int i = 1; i <= n; i++){
int b;
scanf("%lld", &b);
addEdge(i, t, b);
addEdge(t, i, 0);
sum += b;
}
tot = n;
scanf("%lld", &m);
for(int i = 1; i <= m; i++){
int cnt, c1, c2, x;
scanf("%lld%lld%lld", &cnt, &c1, &c2);
sum += c1 + c2;
addEdge(s, tot + 1, c1);
addEdge(tot + 1, s, 0);
addEdge(tot + 2, t, c2);
addEdge(t, tot + 2, 0);
for(int j = 1; j <= cnt; j++){
scanf("%lld", &x);
addEdge(tot + 1, x, INF);
addEdge(x, tot + 1, 0);
addEdge(x, tot + 2, INF);
addEdge(tot + 2, x, 0);
}
tot += 2;
}
n = N - 1;
while(bfs())
ans += dfs(s, INF);
printf("%lld", sum - ans);
return 0;
}
5.洛谷 P3980 [NOI2008] 志愿者招募
这道题目有一个比较好想的上下界费用流做法。我们先把所有种类的志愿者和每一天看成点，根据流量限制模型，我们只需要从每一天向汇点连一条下界为 \(a_i\) 的边，就可以限制第 \(i\) 天至少有 \(a_i\) 名志愿者，再从源点向每类志愿者连一条下界为 \(0\) 的边。最后，我们再从每一类志愿者向 \(s_i\) 到 \(t_i\) 中每一个点连一条下界为 \(0\)，费用为 \(c_i\) 的边，这可以用线段树优化建图。然后跑一遍上下界费用流即可。只不过这样比较难写，而且常数还大。因此我们还有一种普通最大流的做法。
其实这道题目和洛谷 P3358 最长k可重区间集问题很像，我们还是可以从 \(s_i\) 往 \(t_i\) 连边表示一个区间。只是每个点变成了至少要被多少个区间覆盖，且每个点的限制还不一样，我们考虑如何把至少需要 \(a_i\) 个人休息转化成至少怎么样，然后就可以满足网络流的限制。
一个非常人类智慧的方法就是假设有 \(\infty\) 个志愿者，最开始所有人都在休息，那么第 \(i\) 天的限制就变成了至多有 \(\infty - a_i\) 个志愿者在休息。于是我们从第 \(i\) 天往第 \(i + 1\) 天连一条容量为 \(\infty - a_i\) 的边，那么为了保证流量守恒，如果上一个点推过来的流比较大，那么只能多往 \(s_i \rightarrow t_i\) 这些边多推一些流，表示让这些志愿者工作起来，就满足题目限制了。跑一边最大流即可得出答案。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 1e5 + 9, M = 1e5 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, w, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int w){
e[++ecnt] = Edge{v, c, w, head[u]};
head[u] = ecnt;
}
int cur[N], dis[N], n, m, s, t;
queue <int> q;
bool inq[N];
bool spfa();
bool vis[N];
pii dfs(int u, int flow);
int res;
signed main(){
scanf("%lld%lld", &n, &m);
s = n + 2, t = n + 3;
for(int i = 1; i <= n; i++){
int a;
scanf("%lld", &a);
addEdge(i, i + 1, INF - a, 0);
addEdge(i + 1, i, 0, 0);
}
for(int i = 1; i <= m; i++){
int l, r, c;
scanf("%lld%lld%lld", &l, &r, &c);
addEdge(l, r + 1, INF, c);
addEdge(r + 1, l, 0, -c);
}
addEdge(s, 1, INF, 0);
addEdge(1, s, 0, 0);
addEdge(n + 1, t, INF, 0);
addEdge(t, n + 1, 0, 0);
n += 3;
while(spfa()){
pii tmp = dfs(s, INF);
res += tmp.second;
}
printf("%lld", res);
return 0;
}
6.洛谷 P4043 [AHOI2014/JSOI2014] 支线剧情
一道比较模板的有源汇上下界最小费用可行流题目，我们建立出汇点，超级源汇点，从每个剧情结束点向汇点连边，然后直接根据之前的讲解建图即可。
由于是第一次写上下界费用流的题，因此这次把模板部分也粘贴了上来：
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 5e4 + 9, M = 2e5 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, w, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int w){
e[++ecnt] = Edge{v, c, w, head[u]};
head[u] = ecnt;
}
int cur[N], dis[N], n, m, s, t, S, T;
queue <int> q;
bool inq[N];
bool spfa(){
for(int i = 1; i <= n; i++){
dis[i] = INF;
}
q.push(S);
inq[S] = true;
dis[S] = 0;
while(!q.empty()){
int u = q.front();
q.pop();
cur[u] = head[u];
inq[u] = false;
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(e[i].c > 0 && dis[v] > dis[u] + e[i].w){
dis[v] = dis[u] + e[i].w;
if(!inq[v]){
q.push(v);
inq[v] = true;
}
}
}
}
return dis[T] != INF;
}
bool vis[N];
pii dfs(int u, int flow){
if(u == T)
return mk(flow, 0);
int res = 0, val = 0;
vis[u] = 1;
for(int &i = cur[u]; i; i = e[i].nex){
int v = e[i].v;
if(!vis[v] && dis[v] == dis[u] + e[i].w && e[i].c){
pii k = dfs(v, min(e[i].c, flow));
if(!k.first)
continue;
res += k.first;
flow -= k.first;
val += e[i].w * k.first + k.second;
e[i].c -= k.first;
e[i ^ 1].c += k.first;
if(!flow)
break;
}
}
vis[u] = 0;
if(!res){
dis[u] = INF;
}
return mk(res, val);
}
int deg[N], ans, res;
signed main(){
scanf("%lld", &n);
s = 1, t = n + 1, S = n + 2, T = n + 3;
for(int i = 1; i <= n; i++){
int k;
scanf("%lld", &k);
for(int j = 1; j <= k; j++){
int v, w;
scanf("%lld%lld", &v, &w);
addEdge(i, v, INF, w);
addEdge(v, i, 0, -w);
deg[i]--, deg[v]++;
res += w;
}
addEdge(i, t, INF, 0);
addEdge(t, i, 0, 0);
}
for(int i = 1; i <= n; i++){
if(deg[i] > 0){
addEdge(S, i, deg[i], 0);
addEdge(i, S, 0, 0);
}
if(deg[i] < 0){
addEdge(i, T, -deg[i], 0);
addEdge(T, i, 0, 0);
}
}
addEdge(t, s, INF, 0);
addEdge(s, t, 0, 0);
n += 3;
while(spfa()){
pii tmp = dfs(S, INF);
ans += tmp.first;
res += tmp.second;
}
printf("%lld", res);
return 0;
}
7.洛谷 P3153 [CQOI2009] 跳舞
我们首先把男生女生分开考虑，由于一个人最多只会和 \(k\) 个他不喜欢的人跳舞，这启示我们将一个人拆点，拆成喜欢和不喜欢两个点，并从喜欢点向不喜欢点连一条容量为 \(k\) 的边，这就限制了从不喜欢点向外最多只会连 \(k\) 条边。我们再从男生喜欢点向喜欢的女生喜欢点连边，从男生不喜欢点向不喜欢的女生不喜欢点连边，容量都为 \(1\)。
不过此时这个问题不太好解，因为如果建立超级源点向每个男生喜欢点连边，每条边容量设为 \(\infty\)（女生同理），跑最大流的话，每个男生流出的流量可能不相同，而题目规定每个男生流出的流量必须相同。那么此时我们就可以二分答案（其实这道题答案不算大，最多只有 \(n\)，因此可以直接枚举一遍），将超级源点向每个男生喜欢点连的边的流量都设为 \(mid\)，这样跑一边最大流，如果流量是 \(n \times mid\)，就证明所有男生流出的流量相同，就可以更新答案了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 9, M = 1e5 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, k, s, t;
bool bfs();
int dfs(int u, int flow);
int ans;
vector <int> vec;
signed main(){
scanf("%lld%lld", &n, &k);
s = 4 * n + 1, t = 4 * n + 2;
for(int i = 1; i <= n; i++){
addEdge(s, i, 1);
vec.push_back(ecnt);
addEdge(i, s, 0);
addEdge(i, i + n, k);
addEdge(i + n, i, 0);
addEdge(i + 2 * n, t, 1);
vec.push_back(ecnt);
addEdge(t, i + 2 * n, 0);
addEdge(i + 3 * n, i + 2 * n, k);
addEdge(i + 2 * n, i + 3 * n, 0);
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
char c;
cin >> c;
if(c == 'N'){
addEdge(i + n, j + 3 * n, 1);
addEdge(j + 3 * n, i + n, 0);
} else {
addEdge(i, j + 2 * n, 1);
addEdge(j + 2 * n, i, 0);
}
}
}
while(true){
int res = 0;
while(bfs())
res += dfs(s, INF);
if(res != n)
break;
ans++;
for(int i = 0; i < (int)vec.size(); i++){
int num = vec[i];
e[num].c++;
}
}
printf("%lld", ans);
return 0;
}
8.洛谷 P5458 [BJOI2016] 水晶
每次听别人讲网络流，讲到这道题时都叫我们自行看题，看来这道题目确实是又臭又长。
首先，这道题目的多个坐标可能对应一个点，具体一点说，就是 \(x, y, z\) 坐标同时加上或减去一个数，它表示的还是同一个格子，因此我们将 \(x, y, z\) 坐标同时减去 \(z\)，那么所有格子的 \(z\) 坐标就都是 \(0\) 了，此时我们就将这个 \(3\) 维坐标 \((x, y, z)\) 转化成了 \(2\) 维坐标 \((x - z, y - z)\)，且此时一个坐标就对应一个格子。
其次我们考虑 \(3\) 个有水晶的格子，如果它们要形成共振，如果排列成三角形，那么这 \(3\) 个格子一定是 \((x, y)\)，\((x, y - 1)\)（或 \((x - 1, y)\)），\((x - 1, y - 1)\)，那它们的横纵坐标之和就是 \(x + y, x + y - 1, x + y - 2\)，显而易见，它们构成了一个 \(\bmod \, 3\) 的剩余系；如果排列成直线形，那么这 \(3\) 个格子一定是 \((x, y)\)，\((x, y - 1)\)（或 \((x - 1, y)\)），\((x, y + 1)\)（或 \((x + 1, y)\)），那它们的横纵坐标之和就是 \(x + y, x + y + 1, x + y - 1\)，显而易见，它们也构成了一个 \(\bmod \, 3\) 的剩余系。这就说明，如果 \(3\) 个水晶相邻且横纵坐标之和 \(\bmod \, 3\) 分别是 \(0, 1, 2\)，那么它们就会产生共振。
现在题目信息转化得差不多了，考虑到题目要求剩余价值最大，这不难想到最小割模型，而且由于权值在点上，这启示我们要拆点。我们将每个水晶拆成入点和出点，中间连一条容量为价值的边。我们再建立出源点和汇点，从源点向每个横纵坐标之和 \(\bmod \, 3 = 1\) 的水晶的入点连边，再从每个横纵坐标之和 \(\bmod \, 3 = 1\) 的水晶的出点向每个横纵坐标之和 \(\bmod \, 3 = 0\) 的水晶的入点连边，接着从每个横纵坐标之和 \(\bmod \, 3 = 1\) 的水晶的出点向每个横纵坐标之和 \(\bmod \, 3 = 2\) 的水晶的入点连边，最后再从每个横纵坐标之和 \(\bmod \, 3 = 2\) 的水晶的出点向汇点连边，边全都是 \(\infty\)。此时 \(3\) 个会产生共振的水晶就会构成一条路径，必须割掉一条边。此时跑一遍最大流就可以得出答案。
最后一点，就是一个点可能会有多个水晶，我们只需要从这些水晶中选一个出来，并从这个水晶的出点向其他水晶的出点连容量为 \(\infty\) 边即可，这样就可以将这两个水晶合并在一起了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 1e5 + 9, M = 1e6 + 9, K = 6e3 + 9, INF = 1e18 + 9;
struct Edge{
int v, nex;
double c;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, double c){
e[++ecnt] = Edge{v, head[u], c};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, s, t;
bool bfs();
double dfs(int u, double flow);
int x[N], y[N], z[N], tmp[N], tot, d[6][2] = {{-1, -1}, {0, -1}, {1, 0}, {1, 1}, {0, 1}, {-1, 0}};
double c[N], sum, ans;
map <pii, int> id;
signed main(){
scanf("%lld", &n);
s = n * 2 + 1, t = n * 2 + 2;
for(int i = 1; i <= n; i++){
scanf("%lld%lld%lld%lf", &x[i], &y[i], &z[i], &c[i]);
x[i] -= z[i], y[i] -= z[i];
if(((x[i] + y[i]) % 3 + 3) % 3 == 0)
c[i] += c[i] * 0.1;
sum += c[i];
if(id[mk(x[i], y[i])]){
addEdge(id[mk(x[i], y[i])] + n, i + n, INF);
addEdge(i + n, id[mk(x[i], y[i])] + n, 0);
} else
id[mk(x[i], y[i])] = i;
addEdge(i + n, i, c[i]);
addEdge(i, i + n, 0);
}
for(int i = 1; i <= n; i++){
if(((x[i] + y[i]) % 3 + 3) % 3 == 1){
addEdge(s, i + n, INF);
addEdge(i + n, s, 0);
} else if(((x[i] + y[i]) % 3 + 3) % 3 == 2){
addEdge(i, t, INF);
addEdge(t, i, 0);
}
}
for(int i = 1; i <= n; i++){
if(((x[i] + y[i]) % 3 + 3) % 3 == 1){
for(int j = 0; j < 6; j++){
int dx = x[i] + d[j][0];
int dy = y[i] + d[j][1];
if(id[mk(dx, dy)] && ((dx + dy) % 3 + 3) % 3 == 0){
addEdge(i, id[mk(dx, dy)] + n, INF);
addEdge(id[mk(dx, dy)] + n, i, 0);
}
}
}
if(((x[i] + y[i]) % 3 + 3) % 3 == 0){
for(int j = 0; j < 6; j++){
int dx = x[i] + d[j][0];
int dy = y[i] + d[j][1];
if(id[mk(dx, dy)] && ((dx + dy) % 3 + 3) % 3 == 2){
addEdge(i, id[mk(dx, dy)] + n, INF);
addEdge(id[mk(dx, dy)] + n, i, 0);
}
}
}
}
while(bfs())
ans += dfs(s, INF);
printf("%.1lf", sum - ans);
return 0;
}
9.洛谷 P2805 [NOI2009] 植物大战僵尸
依然是一道题面又臭又长的题目，不过这道题的建模要简单一些。
我们将每个植物看成一个点，点权为吃掉这个植物的收益。我们再从一个植物 \(u\) 向所有它保护的植物 \(v\) 连一条边，表示必须吃掉植物 \(u\) 才能吃掉 \(v\)。注意，这里的保护还包括一个植物在另一个植物的前面，这样必须吃掉前面的植物才能吃掉后面的植物。
我们注意到植物的能源可能是负数，但是有些时候吃掉一个能源为负数的植物，就可以去吃掉更多能源为正数的植物。这一看就是我们之前讲到的最大权闭合子图模型。
不过这道题目中可能会出现多个植物互相保护的情况，这样我们就一个植物都吃不了。但是根据最大权闭合子图的定义，一个强连通分量也是一个闭合子图，就会被算进答案。因此，我们先跑一遍 Tarjan 缩点，将所有大小大于 \(2\) 的强连通分量忽略，再对于每个点权 $ p_u$ 大于 \(0\) 的点，我们从 \(s\) 往 \(u\) 连一条容量为 \(p_u\) 的边；对于每个点权 \(p_u\) 小于 \(0\) 的点，我们从 \(u\) 往 \(t\) 连一条容量为 \(-p_u\) 的边就可以了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6 + 9, M = 1e6 + 9, K = 39, INF = 1e18 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
struct edge{
int v, nex;
} e2[M << 1];
int head2[N], ecnt2;
void addEdge2(int u, int v){
e2[++ecnt2] = edge{v, head2[u]};
head2[u] = ecnt2;
}
int cur[N], dep[N], n, m, s, t;
bool bfs();
int dfs(int u, int flow);
int low[N], dfn[N], dfncnt;
stack <int> sta;
bool ins[N];
int scc[N], sc;
void tarjan(int u){
low[u] = dfn[u] = ++dfncnt;
sta.push(u);
ins[u] = true;
for(int i = head2[u]; i; i = e2[i].nex){
int &v = e2[i].v;
if(!dfn[v]){
tarjan(v);
low[u] = min(low[u], low[v]);
} else if(ins[v])
low[u] = min(low[u], dfn[v]);
}
if(low[u] == dfn[u]){
if(sta.top() == u){
ins[sta.top()] = 0;
sta.pop();
} else {
++sc;
while(sta.top() != u){
scc[sta.top()] = sc;
ins[sta.top()] = 0;
sta.pop();
}
scc[sta.top()] = sc;
ins[sta.top()] = 0;
sta.pop();
}
}
}
int id(int x, int y){
return (x - 1) * m + y;
}
int c[K][K], siz[N], sum, ans;
signed main(){
scanf("%lld%lld", &n, &m);
s = n * m + 1, t = n * m + 2;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
scanf("%lld%lld", &c[i][j], &siz[id(i, j)]);
for(int k = 1; k <= siz[id(i, j)]; k++){
int a, b;
scanf("%lld%lld", &a, &b);
a++, b++;
addEdge2(id(a, b), id(i, j));
}
if(j != 1)
addEdge2(id(i, j - 1), id(i, j));
}
}
for(int i = 1; i <= n * m; i++)
if(!dfn[i])
tarjan(i);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
if(!scc[id(i, j)]){
if(c[i][j] > 0){
sum += c[i][j];
addEdge(s, id(i, j), c[i][j]);
addEdge(id(i, j), s, 0);
} else {
addEdge(id(i, j), t, -c[i][j]);
addEdge(t, id(i, j), 0);
}
}
for(int k = head2[id(i, j)]; k; k = e2[k].nex){
int v = e2[k].v;
addEdge(id(i, j), v, INF);
addEdge(v, id(i, j), 0);
}
}
}
while(bfs())
ans += dfs(s, INF);
printf("%lld", max(sum - ans, 0ll));
return 0;
}
10.洛谷 P3305 [SDOI2013] 费用流
第一问直接跑网络最大流就可以了，我们考虑第 \(2\) 问。很显然，\(\text{Bob}\) 一定会将所有花费 \(P\) 全部加在流量最大的边上。那么 \(\text{Alice}\) 的最优策略就出来了，那就是在最大流不变的情况下，让流量最大的边的流量尽可能小。
由于要让最大值最小，因此我们考虑二分答案。不过直接二分最大流不是那么好搞，因此我们考虑改变每条边的容量来间接改变最大流。一个显然的事实就是我们最终确定出的最大流一定至少有一条边流了 \(mid\) 的流量，否则还可以从原点找到增广路来增广。因此我们二分出容量上限 \(mid\)，将所有容量大于 \(mid\) 的边改为 \(mid\)，跑一遍网络最大流。如果这个时候最大流没有变，那么就将答案更新为 \(mid \times P\)。
最后，这道题要用到实数二分，细节比较多，要多加小心啊。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e2 + 9, M = 5e3 + 9, INF = 1e18 + 9;
const double eps = 1e-6;
struct Edge{
int v, nex;
double c;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, double c){
e[++ecnt] = Edge{v, head[u], c};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, p, s, t;
bool bfs();
double dfs(int u, double flow);
int fl[M];
double ans;
vector <int> vec;
signed main(){
scanf("%lld%lld%lld", &n, &m, &p);
s = 1, t = n;
for(int i = 1; i <= m; i++){
int u, v, c;
scanf("%lld%lld%lld", &u, &v, &c);
addEdge(u, v, c);
vec.push_back(ecnt);
fl[ecnt] = c;
addEdge(v, u, 0);
}
while(bfs())
ans += dfs(s, INF);
double l = 0, r = 5e4, res = 0;
while(fabs(l - r) > eps) {
double mid = (l + r) / 2;
for(int i : vec){
e[i].c = min(mid, 1.0 * fl[i]);
e[i ^ 1].c = 0;
}
double tmp = 0;
while(bfs())
tmp += dfs(s, INF);
if(fabs(tmp - ans) < 10 * eps){
res = mid;
r = mid - eps;
} else
l = mid + eps;
}
printf("%0.0f\n%0.4lf", ans, res * p);
return 0;
}
11.洛谷 P2153 [SDOI2009] 晨跑
这道题是一个特别模板的拆点的题目。我们将 \(1\) 号点和 \(n\) 号点经过的次数设为 \(\infty\)，其他设成 \(1\)，跑一遍最小费用最大流即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair <int, int>
#define mk make_pair
const int N = 5e3 + 9, M = 5e4 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, w, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c, int w){
e[++ecnt] = Edge{v, c, w, head[u]};
head[u] = ecnt;
}
int cur[N], dis[N], n, m, s, t;
queue <int> q;
bool inq[N];
bool spfa();
bool vis[N];
pii dfs(int u, int flow);
int ans, res;
signed main(){
scanf("%lld%lld", &n, &m);
s = n + 1, t = n;
for(int i = 1; i <= m; i++){
int u, v, w;
scanf("%lld%lld%lld", &u, &v, &w);
addEdge(u, v + n, 1, w);
addEdge(v + n, u, 0, -w);
}
for(int i = 1; i <= n; i++){
if(i == n || i == 1){
addEdge(i + n, i, INF, 0);
addEdge(i, i + n, 0, 0);
} else {
addEdge(i + n, i, 1, 0);
addEdge(i, i + n, 0, 0);
}
}
n = n * 2;
while(spfa()){
pii tmp = dfs(s, INF);
ans += tmp.first;
res += tmp.second;
}
printf("%lld %lld", ans, res);
return 0;
}
12.洛谷 P6054 [RC-02] 开门大吉
由于要让总权值最小，因此我们考虑最小割模型。
因为每个选手答对每套题目的概率不一样，那么答第 \(j\) 套题目时的选手 \(i\) 和答第 \(j - 1\) 套题目的选手 \(i\) 不一样了。根据P2053 [SCOI2007] 修车的思路，我们将一个选手 \(i\) 拆成 \(m + 1\) 个点 \((i, j)(j \in [0, m])\)，我们从 \((i, j)\) 向 \((i, j + 1)\) 连边，容量为 \(\displaystyle\sum_{k = 1}^p c_k \prod_{pr = 1}^k p_{i, j, pr}\)，表示第 \(i\) 个人做第 \(j\) 套题目的期望得分，而割掉这条边就表示第 \(i\) 个人做了第 \(j\) 套题目，我们再从源点向所有的 \((i, 1)\) 连边，流量为 \(\infty\)；\((i, m + 1)\) 向汇点连边，流量为 \(\infty\)。这样每一条路径都会割掉一条边，保证了每个人做一套题目。
此时我们考虑如何满足第 \(i\) 位选手的套题编号必须至少比第 \(j\) 位的大 \(k\) 的限制。此时我们需要限制两条割边的相对位置。因此我们对于所有限制 \((i, j, k)\)，都从每个 \((j, x)(x \in [0, m])\) 向 \((i, \min(x + k, m + 1))\) 连一条容量为 \(\infty\) 边构造出一条新的路径。此时，如果我们选择 \((j, x)\) 到 \((j, x + 1)\) 这条边割掉，那么现在还存在一条 \(s \leadsto (j, x) \rightarrow (i, x + k) \leadsto t\) 的路径，那么此时如果要割掉 \((i, x + k) \leadsto t\) 一侧的边时，那么一定割掉的是套题编号 \(\geq x + k\) 的边，满足了题目要求。
不过现在又有一个问题，那就是一个选手可能会做多套题目，我们考虑一下这种情况。
首先，如果没有 \((i, j, k)\) 的限制，根据贪心，每条路径只会割掉一条边。加上限制后我们依然会割掉这些边，但是限制是有传递性的于是我们从每个 \((i, j + 1)\) 向 \((i, j)\) 连一条容量为 \(\infty\) 的边。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 9, M = 1e5 + 9, K = 89, INF = 1e18 + 9;
struct Edge{
int v;
double c;
int nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, double c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, p, y, s, t;
bool bfs();
double dfs(int u, double flow);
int c[K], T;
double ans, f[K][K][K];
int id(int i, int j){
return (i - 1) * (m + 1) + j;
}
void init(){
for(int i = 1; i <= n; i++)
head[i] = 0;
ecnt = 1;
ans = 0;
}
signed main(){
scanf("%lld", &T);
while(T--){
init();
scanf("%lld%lld%lld%lld", &n, &m, &p, &y);
for(int i = 1; i <= p; i++)
scanf("%lld", &c[i]);
for(int j = 1; j <= m; j++)
for(int i = 1; i <= n; i++)
for(int k = 1; k <= p; k++)
scanf("%lf", &f[i][j][k]);
s = n * (m + 1) + 1, t = n * (m + 1) + 2;
for(int i = 1; i <= n; i++){
addEdge(s, id(i, 1), INF);
addEdge(id(i, 1), s, 0);
addEdge(id(i, m + 1), t, INF);
addEdge(t, id(i, m + 1), 0);
for(int j = 1; j <= m; j++){
double pr = 1;
addEdge(id(i, j + 1), id(i, j), INF);
addEdge(id(i, j), id(i, j + 1), 0);
double sum = 0;
for(int k = 1; k <= p; k++){
pr *= f[i][j][k];
sum += pr * c[k];
}
addEdge(id(i, j), id(i, j + 1), sum);
addEdge(id(i, j + 1), id(i, j), 0);
}
}
for(int i = 1; i <= y; i++){
int a, b, x;
scanf("%lld%lld%lld", &a, &b, &x);
for(int t = 1; t <= m; t++){
if(t + x >= 1 && t + x <= m + 1){
addEdge(id(b, t), id(a, t + x), INF);
addEdge(id(a, t + x), id(b, t), 0);
}
}
}
bool flag = false;
n = n * (m + 1) + 2;
while(bfs()){
ans += dfs(s, INF);
if(ans >= INF){
printf("-1\n");
flag = true;
break;
}
}
if(!flag){
if(ans >= INF)
printf("-1\n");
else
printf("%.4lf\n", ans);
}
}
return 0;
}
13.洛谷 P4298 [CTSC2008] 祭祀
这就是一个 \(\text{DAG}\) 最小相交路径覆盖的板子题，只是输出方案有点麻烦。
对于第 \(3\) 问，我们可以枚举每个点，将这个点删去后如果答案减小了，那么就说明这个点可以作为祭祀点。对于第 \(2\) 问，我们可以在第 \(3\) 问的答案中，将可以被经过别的祭祀点的流流经的祭祀点删去，就可以得到一组可行解。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e2 + 9, M = 5e3 + 9, INF = 1e18 + 9;
struct Edge{
int v, c, nex;
} e[M << 1];
int head[N], ecnt = 1;
void addEdge(int u, int v, int c){
e[++ecnt] = Edge{v, c, head[u]};
head[u] = ecnt;
}
int cur[N], dep[N], n, m, s, t;
bool bfs();
int dfs(int u, int flow);
int vis[N], tmp1[N], tmp2[N], ans;
bool plan[N], flag[N];
bitset <N> w[N];
signed main(){
scanf("%lld%lld", &n, &m);
s = 2 * n + 1, t = 2 * n + 2;
for(int i = 1; i <= m; i++){
int u, v;
scanf("%lld%lld", &u, &v);
w[u][v] = 1;
}
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
if(w[i][k])
w[i] = w[i] | w[k];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if(w[i][j]){
addEdge(i, j + n, 1);
addEdge(j + n, i, 0);
}
for(int i = 1; i <= n; i++){
addEdge(s, i, 1);
tmp1[i] = ecnt;
addEdge(i, s, 0);
addEdge(i + n, t, 1);
tmp2[i] = ecnt;
addEdge(t, i + n, 0);
}
n = n * 2 + 2;
while(bfs())
ans += dfs(s, INF);
n = (n - 2) / 2;
printf("%lld\n", n - ans);
for(int i = 1; i <= n; i++){
memset(head, 0, sizeof(head));
ecnt = 1;
for(int j = 1; j <= n; j++)
for(int k = 1; k <= n; k++)
if(w[j][k]){
addEdge(j, k + n, 1);
addEdge(k + n, j, 0);
}
for(int j = 1; j <= n; j++){
addEdge(s, j, 1);
addEdge(j, s, 0);
addEdge(j + n, t, 1);
addEdge(t, j + n, 0);
}
int cnt = n, tmp = 0;
for(int j = 1; j <= n; j++)
if(w[i][j] || w[j][i] || i == j){
e[tmp1[j]].c = 0;
e[tmp2[j]].c = 0;
cnt--;
}
n = n * 2 + 2;
while(bfs())
tmp += dfs(s, INF);
n = (n - 2) / 2;
if(cnt - tmp == n - ans - 1)
flag[i] = 1;
}
for(int i = 1; i <= n; i++)
plan[i] = flag[i];
for(int i = 1; i <= n; i++)
if(plan[i] == 1)
for(int j = 1; j <= n; j++)
if(w[i][j] || w[j][i])
plan[j] = 0;
for(int i = 1; i <= n; i++)
printf("%lld", (int)plan[i]);
printf("\n");
for(int i = 1; i <= n; i++)
printf("%lld", (int)flag[i]);
return 0;
}
网络流与贪心
参考资料
-
谭 qx、张 hr、付 ym、王 yh 的课件
-
Introduction to Algorithms(Third Edition) Thomas H.Cormen、Charles E.leiserson、Ronald L.Rivest、Clifford Stein
-
《算法竞赛》 罗勇军、郭卫斌
-
二分图最大匹配 OI Wiki
-
二分图最大权匹配 OI Wiki
-
Dinitz' Algorithm：The original Version and Even's Version Yefim Dinitz
-
网络流，二分图与图的匹配 Alex_wei
-
图论——二分图——最小点覆盖 Probie Tao
-
二分图知识点：一篇笔记带你回顾 Hacking Group 0318
-
【模板】最大权闭合子图 jimmyywang
-
题解 P2050 【[NOI2012]美食节】 Froggy
本文来自博客园，作者：Orange_new，转载请注明原文链接：https://www.cnblogs.com/JPGOJCZX/p/18422848
浙公网安备 33010602011771号