DP 学习笔记(一):DP 基础知识,基础 DP 类型
基本概念
动态规划是一种非常常见的算法,它将大问题划分为与它一样但数据规模更小的小问题,而大问题的的最优解决方案又来自于小问题的最优解决方案。简称为 DP(Dynamic Programming)。
动态规划优于暴力枚举的原因是它对于每一个问题,不是从头开始解决,而是基于之前解决的规模更小问题计算得来,这可以大大降低时间复杂度,而思维难度则上升了不止一个难度,而且它可以与数学(概率 DP)、字符串(自动机 DP)、图论(最短路算法)、数据结构(数据结构优化 DP)等多种信息竞赛中的重要版块进行深度融合,因此需要我们认真学习。
一些定义
状态:当前所求问题的信息;
函数:当前所求问题的答案,一般叫做 DP 值;
状态转移方程:如何通过当前所求问题的状态,找到它可以由哪几个小问题推出,并通过那几个小问题的函数推出当前问题的函数。一般用一个递推式子表示。
时间复杂度:\(=\) 状态个数 \(\times\) 转移时间复杂度。
DP 能解决的问题一般具有以下 \(3\) 点性质,下面通过斐波那契数列的求解过程来说明。
斐波那契数列是一种具有递推关系的数列,它的每一个数字都是前两个数字的和:\(1, 1, 2, 3, 5, 8, \dots\)。用函数表示出来就是 \(f_i = f_{i - 1} + f_{i - 2}\),那么它具有以下性质:
重叠子问题
简单来说,就是求解大问题的最优解决方案时,需要将大问题拆分成若干个小问题,小问题会被拆分成更小的问题,这些拆分出的小问题可能会有重复。比如求解斐波那契数列的第五项 \(f_5\):
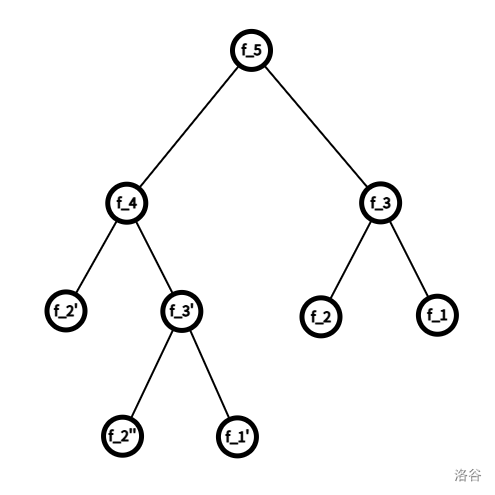
可以发现,\(f_3\) 被计算了两遍,其实只用计算一遍就可以了,这就是 DP 可以实现较优复杂度的原因,这在小数据规模时还不明显,在数据规模大时就可以极大优化代码。
最优子结构
首先,大问题的最优解包含小问题的最优解,也就是当大问题取得最优解时,小问题也取得最优解。其次,小问题的最优解可以推出大问题的最优解,这就是最优子结构。
在斐波那契数列的求解过程中,求 \(f_i\) 可以拆成求规模更小的 \(f_{i - 1}\) 和 \(f_{i - 2}\),而 \(f_{i - 1}\) 和 \(f_{i - 2}\) 又可以加起来等于 \(f_i\),这样就符合最优子结构。
无后效性
简单来说,就是当我们求出某个问题的最优解时,我们就不再关心这个最优解是如何得到的,也就不再改变这个值了,而是将这个解作为已知继续推出其它问题的最优解。
求解斐波那契数列的过程中,当我们求出 \(f_i\) 的值以后,这个值我们就不再改了。当我们要求 \(f_{i + 1}\) 和 \(f_{i + 2}\),直接把 \(f_i\) 的值拿来用就行了,这就符合最优子结构。
无后效性是可以使用 DP 的前提条件,当后续的操作会影响到之前操作的值时,就无法通过重叠子问题来优化枚举的复杂度,也就无法使用 DP。一般求解 DP 问题都需要考虑 DP 的顺序,让问题没有后效性。
DP 一般有以下 \(3\) 种写法:
记忆化搜索
在搜索时,如果遇到之前求解过的状态,就直接将它的 DP 值拿来用,而不用继续往下递归。
求解斐波那契数列的记忆化搜索代码:
int f[N];
int fib(int x){
if(x == 1 || x == 2)
return 1;
if(f[x])
return x;
else
return fib(x - 1) + fib(x - 2);
}
填表法
考虑当前状态是由哪几个状态转移而来。
求解斐波那契数列的填表法代码:
int f[N];
f[1] = f[2] = 1;
for(int i = 3; i <= n; i++)
f[i] = f[i - 1] + f[i - 2];
填表法也是最常见的 DP 写法。
刷表法
考虑当前状态会影响到后续哪几个状态的求解。
求解斐波那契数列的刷表法代码:
int f[N];
f[1] = 1;
for(int i = 1; i <= n; i++){
f[i + 1] += f[i];
f[i + 2] += f[i];
}
背包 DP
一类非常经典的线性 DP 题,因此专门提出来讲。
一些定义:\(n\) 表示物品个数,\(m\) 表示背包总容量,\(w_i\) 表示物品重量,\(v_i\) 表示物品价值,\(c_i\) 表示物品个数,\(f\) 表示 DP 函数(代码中为 dp)。
01背包
记 \(f_{i, j}\) 表示考虑前 \(i\) 个物品,总重量为 \(j\) 的最大价值,考虑当前物品选还是不选,那么可以很轻松写出状态转移方程:\(f_{i, j} = \max(f_{i - 1, j}, f_{i - 1, j - w_i} + v_i)\)。
完整代码:
#include <bits/stdc++.h>
using namespace std;
const int M = 109, T = 1009;
int w[M], v[M], dp[M][T], n, m;
int main(){
scanf("%d%d", &m, &n);
for(int i = 1; i <= n; i++)
scanf("%d%d", &w[i], &v[i]);
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++){
if(w[i] > j)
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j - w[i]] + v[i], dp[i - 1][j]);
}
printf("%d", dp[n][t]);
return 0;
}
滚动数组优化01背包
滚动数组可以优化背包的空间复杂度。
可以发现,\(f_{i, j}\) 的值只与 \(f_{i - 1}\) 这一行有关系,与 \(i - 2, i - 3, \dots, 1\) 这些行都没有关系,那么我们可以只存当前枚举的行上一行的信息,就可以实现空间优化。滚动数组一般有以下两种写法:
交替滚动
开两行数组,一行存计算过的旧的一行,一行存当前计算的一行。
完整代码:
int dp[2][N];
int now = 0, old = 1;
for(int i = 1; i <= n; i++){
swap(old, now);
for(int j = 0; j <= m; j++){
if(w[i] > j)
dp[now][j] = dp[old][j];
else
dp[now][j] = max(dp[old][j], dp[old][j - w[i]] + v[i]);
}
}
自我滚动
只开一行,一边计算,一边更新。这时候内层循环要倒着来枚举,下面来说明。
考虑当前状态由那些状态更新来:
发现 \(f_{i, j}\) 可能会从 \(f_{i - 1, j - k}\) 转移过来,而从前往后枚举会更新掉 \(f_{i - 1, j - k}\),导致转移错误,因此只能从后往前枚举
完整代码:
int dp[N];
for(int i = 1; i <= n; i++)
for(int j = m; j >= w[i]; j--)
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
bitset优化01背包
当我们在求解某类 \(01\) 背包时,只需要判断某种状态是否可以达到(比如[ABC221G] Jumping sequence),这时就可以用 \(bitset\) 将时间复杂度优化成 \(O(\frac{n^2}{\omega})\),其中 \(\omega = 32\)。
首先,这种可行性的背包的转移方程就是 \(f_j = \max(f_j, f_{j - w_i} + v_i)\),因为只用判断当前状态可否到达,因此 \(f_j\) 的值只有 \(0\) 和 \(1\) 两种,那么转移方程可以简化成 \(f_j = f_{j - w_i} \mid f_j\)。
\(bitset\) 顾名思义,就是存储 \(0\) 和 \(1\) 的集合,其内部是一个值只有 \(0\) 或 \(1\) 的数组,可以用 bitset <size> name 来定义,可以发现,\(f_j \mid f_{j - w_i}\) 相当于是将当前 DP 数组左移 \(w_i\) 位,再或起来,而 \(bitset\) 也支持将整个数组左右移动,复杂度为 \(O(\frac{len}{\omega})\),那么,我们只需要将循环的第二层改为将当前 \(bitset\) 异或上 \(bitset\) 左移 \(w_j\) 位,就可以将复杂度优化了。
完整代码:
bitset <50000> b;
b.set(0, 1);
for(int i = 1; i <= n; i++)
b |= (b << w[i]);
完全背包
考虑现在不止一个物品,而是有无穷个物品,但背包有个总容量,因此每个物品最多放 \(\frac{m}{w_i}\) 个,那么考虑在 \(01\) 背包的基础上再枚举一遍物品个数。
还是记 \(f_{i, j}\) 表示考虑前 \(i\) 个物品,总重量为 \(j\) 的最大价值,考虑当前物品选几个,那么可以写出状态转移方程 \(f_{i, j} = f_{i - 1, j - k \times w_i} + k \times v_i(0 \leq k \leq \frac{j}{w_i})\),不过复杂度是 \(O(n^3)\),需要优化。
其实,考虑 \(f_{i, j}\) 的转移方程 \(f_{i, j} = f_{i - 1, j - k \times w_i} + k \times v_i(0 \leq k \leq \frac{j}{w_i})\) 可以写作 \(f_{i, j} = \max(f_{i - 1, j}, v_i + f_{i - 1, j - w_i - k' \times w_i} + k' \times v_i)(0 \leq k' \leq \frac{j - w_i}{w_i})\),将 \(\max\) 中后半部分与 \(f_{i, j - w_i}\) 的转移方程 \(f_{i, j - w_i} = f_{i - 1, j - w_i - k \times w_i} + k \times v_i)(0 \leq k \leq \frac{j - w_i}{w_i})\) 相比较,可以发现原先的表达式被简化成了 \(f_{i, j} = \max(f_{i - 1, j}, f_{i, j - w_i} + v_i)\),现在就可以 \(O(n^2)\) 通过本题了。
由于考虑到 \(f_{i, j}\) 可能会从同一排靠前的位置转移而来,因此用滚动数组优化时,\(j\) 这一维需要正序枚举。
当然,可行性的完全背包也可以用 \(bitset\) 优化,这里不再赘述。
完整代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e7 + 5;
long long v[N], w[N], dp[N], n, m;
int main() {
scanf("%d%d", &n, &m);
memset(dp, 0, sizeof(dp));
for(int i = 1; i <= n; i++)
cin >> w[i] >> v[i];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
if(j >= w[i])
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
printf("%d", dp[m]);
return 0;
}
由于完全背包中每个物品也不是能选任意多个,因此也可以套用接下来多重背包的优化方式。
多重背包
可以发现这和完全背包很像,但有可能物品取不到 \(\frac{j}{w_i}\) 这么多个,那么此处就无法通过完全背包的方式优化时间复杂度,因为你无法判断 \(f_{i, j - w_i}\) 转移时是否已经选满了 \(c_i\) 个。因此只能枚举当前物品选几个,转移方程 \(f_{i, j} = f_{i - 1, j - k \times w_i} + k \times v_i(0 \leq k \leq \min(c_i, \frac{j}{w_i}))\)。
注意此时的状态是由上一排转移过来,和 \(01\) 背包类似,因此滚动数组优化时需要倒序枚举。
完整代码(会 TLE):
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 9;
int w[N], v[N], c[N], dp[N], n, m;
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%d%d%d", &v[i], &w[i], &c[i]);
for(int i = 1; i <= n; i++)
for(int j = m; j >= w[i]; j--)
for(int k = 1; k <= c[i] && k * w[i] <= j; k++)
dp[j] = max(dp[j], dp[j - k * w[i]] + k * v[i]);
printf("%d", dp[m]);
return 0;
}
二进制拆分优化多重背包
考虑一个物品价值为 \(v\),重量为 \(w\),数量为 \(c\),那么可以发现:
-
当取 \(1\) 个该物品时,重量为 \(w\),价值为 \(v\);
-
当取两个该物品时,重量为 \(2 \times w\),价值为 \(2 \times v\);
-
当取 \(3\) 个该物品时,重量为 \(3 \times w = 2 \times w + w\),价值为 \(3 \times v = 2 \times v + v\);
-
当取 \(4\) 个该物品时,重量为 \(4 \times w\),价值为 \(4 \times v\);
-
当取 \(5\) 个该物品时,重量为 \(5 \times w = 4 \times w + w\),价值为 \(5 \times v = 4 \times v + v\);
-
\(\dots\)。
可以发现,对于同一种物品,可以把它二进制拆分成 \(\log_2 c_i\) 个物品,这些物品的重量为 \(2^k \times w\),价值为 \(2^k \times v\),而且它们组合在一起就变成任意个该物品,此时可以通过 \(01\) 背包来做了,复杂度降低为 \(O(m \displaystyle\sum_{i = 1}^n \log_2 c_i)\)
完整代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m, dp[N];
int v[N], w[N], c[N];
int new_n;
int new_v[N], new_w[N], new_c[N];
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%d%d%d", &v[i], &w[i], &c[i]);
int new_n = 0;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= c[i]; j <<= 1){
c[i] -= j;
new_w[++new_n] = j * w[i];
new_v[new_n] = j * v[i];
}
if(c[i]){
new_w[++new_n] = c[i] * w[i];
new_v[new_n] = c[i] * v[i];
}
}
for(int i = 1; i <= new_n; i++)
for(int j = m; j >= new_w[i]; j--)
dp[j] = max(dp[j], dp[j - new_w[i]] + new_v[i]);
printf("%d", dp[m]);
return 0;
}
单调队列优化多重背包
混合背包
将 \(01\) 背包部分看成每个物品最多只能选 \(1\) 个,完全背包部分看成每个物品最多只能选 \(\frac{m}{w_i}\) 个,多重背包部分不变,那么可以直接转化为多重背包。
完整代码(使用了单调队列优化):
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 9;
int n, m, h1, h2, m1, m2;
int dp[N], q[N], num[N];
int w, v, c;
int main(){
scanf("%d:%d %d:%d %d", &h1, &m1, &h2, &m2, &n);
m = 60 * (h2 - h1) + m2 - m1;
for(int i = 1; i <= n; i++){
scanf("%d%d%d", &w, &v, &c);
if(c == 0)
c = 100000000;
if(c > m / w)
c = m / w;
for(int b = 0; b < w; b++){
int head = 1, tail = 1;
for(int y = 0; y <= (m - b) / w; y++){
int tmp = dp[b + y * w] - y * v;
while(head < tail && q[tail - 1] <= tmp)
tail--;
q[tail] = tmp;
num[tail++] = y;
while(head < tail && y - num[head] > c)
head++;
dp[b + y * w] = max(dp[b + y * w], q[head] + y * v);
}
}
}
printf("%d", dp[m]);
return 0;
}
二维费用背包
在 \(01\) 背包的基础上再开一维就可以了。
完整代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 209;
int dp[N][N], w[N], t[N], n, m, T;
int main(){
scanf("%d%d%d", &n, &m, &T);
for(int i = 1; i <= n; i++)
scanf("%d%d", &w[i], &t[i]);
for(int i = 1; i <= n; i++)
for(int j = m; j >= w[i]; j--)
for(int k = T; k >= t[i]; k--)
dp[j][k] = max(dp[j][k], dp[j - w[i]][k - t[i]] + 1);
printf("%d", dp[m][T]);
return 0;
}
分组背包
和 01 背包很像,就是不再枚举每个物品,而是枚举每个组别再枚举这个组别中选哪个物品就可以了。
#include <bits/stdc++.h>
using namespace std;
const int N = 109, M = 1e3 + 9;
int dp[M], w[M], v[M], n, m, cnt;
vector <int> vec[N];
int main(){
scanf("%d%d", &m, &n);
for(int i = 1; i <= n; i++){
int num;
scanf("%d%d%d", &w[i], &v[i], &num);
cnt = max(cnt, num);
vec[num].push_back(i);
}
for(int k = 1; k <= cnt; k++)
for(int j = m; j >= 0; j--)
for(int i = 0; i < vec[k].size(); i++)
if(j >= w[vec[k][i]])
dp[j] = max(dp[j], dp[j - w[vec[k][i]]] + v[vec[k][i]]);
else
dp[j] = dp[j];
printf("%d", dp[m]);
return 0;
}
树形背包 (有依赖的背包)
洛谷 P1064 [NOIP 2006 提高组] 金明的预算方案
这是树形背包的来源,但是这并不是最泛化的树形背包。
由于买附件一定要先买主件,而买主件则没有限制,因此一共有以下 \(5\) 种不同的购买方案:
-
什么都不买;
-
只买主件;
-
买主件和第一个附件(如果有);
-
买主件和第二个附件(如果有);
-
买主件和两个附件(如果都有);
我们依然按照 01 背包的 DP 状态设法,记 \(dp_{i, j}\) 表示考虑前 \(i\) 个主件,总重量为 \(j\) 的最大价值,那么我们就可以写出上面 \(5\) 种情况分别的状态转移方程:
-
\(dp_{i, j} = dp_{i - 1, j}\);
-
\(dp_{i, j} = \max(dp_{i, j}, dp_{i - 1, j - v_{i, 0}} + v_{i, 0} \times p_{i, 0})\);
-
\(dp_{i, j} = \max(dp_{i, j}, dp_{i - 1, j - v_{i, 0} - v_{i, 1}} + v_{i, 0} \times p_{i, 0} + v_{i, 1} \times p_{i, 1})\);
-
\(dp_{i, j} = \max(dp_{i, j}, dp_{i - 1, j - v_{i, 0} - v_{i, 2}} + v_{i, 0} \times p_{i, 0} + v_{i, 2} \times p_{i, 2})\);
-
\(dp_{i, j} = \max(dp_{i, j}, dp_{i - 1, j - v_{i, 0} - v_{i, 1} - v_{i, 2}} + v_{i, 0} \times p_{i, 0} + v_{i, 1} \times p_{i, 1} + v_{i, 2} \times p_{i, 2})\);
注意一下下标,然后这道题就做完了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 3.2e4 + 9, M = 69;
int v[M][3], p[M][3], dp[N], n, m, v1, p1, q1;
signed main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i++){
scanf("%d%d%d", &v1, &p1, &q1);
if(q1){
if(v[q1][1]){
v[q1][2] = v1;
p[q1][2] = p1;
} else {
v[q1][1] = v1;
p[q1][1] = p1;
}
} else {
v[i][0] = v1;
p[i][0] = p1;
}
}
for(int i = 1; i <= m; i++){
for(int j = n; j >= 1; j--){
if(v[i][0] <= j)
dp[j] = max(dp[j], dp[j - v[i][0]] + v[i][0] * p[i][0]);
if(v[i][0] + v[i][1] <= j)
dp[j] = max(dp[j], dp[j - v[i][0] - v[i][1]] + v[i][0] * p[i][0] + v[i][1] * p[i][1]);
if(v[i][0] + v[i][2] <= j)
dp[j] = max(dp[j], dp[j - v[i][0] - v[i][2]] + v[i][0] * p[i][0] + v[i][2] * p[i][2]);
if(v[i][0] + v[i][1] + v[i][2] <= j)
dp[j] = max(dp[j], dp[j - v[i][0] - v[i][1] - v[i][2]] + v[i][0] * p[i][0] + v[i][1] * p[i][1] + v[i][2] * p[i][2]);
}
}
printf("%d", dp[n]);
return 0;
}
这其实也不是特别泛化的树形背包,因为每个课程的重量是 \(1\)。不过重量不是 \(1\) 可以仿照本题思路列出状态转移方程。
首先可以发现,如果按照依赖关系建图的话,会连出一个森林,此时背包间的合并比较麻烦,因此我们建出一个超级根作为所有树根的直接先修课(比如学会如何写字),我们再强制选超级根就行了。因此我们只需要将 \(m\) 增大 \(1\) 即可。
由于是在树上,因此我们就将 DP 函数改成 \(dp_{u, i}\) 表示在 \(u\) 的子树内,选了 \(i\) 门功课的最大学分。那么我们选的这 \(i\) 门功课一定是一个包含根节点的连通块。于是我们考虑 \(u\) 的儿子 \(v\),我们假设我们在 \(v\) 的子树内选了 \(j\) 门功课,那么这 \(j\) 门功课一定与 \(u\) 联通,满足题目的限制。因此状态转移方程就是 \(dp_{u, i} = \displaystyle\max_{j = 0}^{\min(i - 1, siz_v)} dp_{u, i - j} + dp_{v, j}\)。此时我们在 \(\mathcal O(nm^2)\) 的时间复杂度内解决了问题。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 3e2 + 9;
struct Edge{
int v, nex;
} e[N];
int head[N], ecnt;
void addEdge(int u, int v){
e[++ecnt] = Edge{v, head[u]};
head[u] = ecnt;
}
int dp[N][N], n, m;
void DP(int u){
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
DP(v);
for(int i = m + 1; i >= 1; i--)
for(int j = 0; j <= i - 1; j++)
dp[u][i] = max(dp[u][i], dp[u][i - j] + dp[v][j]);
}
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++){
int fa;
scanf("%d%d", &fa, &dp[i][1]);
addEdge(fa, i);
}
DP(0);
printf("%d\n", dp[0][m + 1]);
return 0;
}
泛化物品背包
泛化物品
考虑这样一个物品,它的价值不是一个定值,而是会随着费用的变化而变化。就像同样一套题目,你在一天的早晨和晚上都去做它,效率肯定是不一样的,说明它的价值和时间有关系。这就是泛化物品的概念。
如果从更数学的角度来说,就是我们定义了一个价值函数 \(v = h(w)\),当我们输入不同的 \(w\) 的时候,这个函数会输出对应的 \(v\) 值。其实我们之前讲的很多背包问题,都是泛化物品背包的一种:
-
\(01\) 背包的 \(h\) 函数为 \(v = [w = w_i]v_i\),表示只有当放入物品的费用为 \(w_i\) 时才会获得 \(v_i\) 的收益;
-
多重背包的 \(h\) 函数为 \(v = [w_i \mid w]\left[ \displaystyle\frac{w}{w_i} \leq c_i \right] \displaystyle\frac{wv_i}{w_i}\),表示只有当放入物品的费用为 \(w_i\) 的倍数且选的物品个数 \(\leq c_i\) 时才会获得选的物品个数 \(\times v_i\) 的收益;
-
树形背包例题洛谷 P1064 [NOIP 2006 提高组] 金明的预算方案中,主件和附件一起可以看成一个物品组,你给这个物品组分配不同的花费,就会得到不同的价值,这也是一个泛化背包问题。
泛化物品合并
现在我们要做的,就是选定一个费用,然后把两个泛化物品合并起来,此时我们需要考虑如何将费用分配给这两个物品。
假设分配给这两个物品分别 \(w_1\) 和 \(w——2\) 的费用,那么我们现在要求的最大价值 \(h(w) = h_1(w_1) + h_2(w_2)\),此时我们就得到了一个新的物品,它的价值 \(h(w)\) 受两个泛化物品影响,我们一般通过简化式子,把它变成一个跟 \(w_1 + w_2\) 有关的式子,此时我们从新将 \(w_1 + w_2\) 看成一个整体。然后就可以继续合并了。
对于其中的物品都是泛化物品的背包问题,求它的答案的过程也就是求所有这些泛化物品之和的过程。假设最后合成的泛化物品的价值为 \(h_n(w_1 + w_2 + \dots + w_n) = h_n(w)\),那么我们只需要枚举一遍 \(w\) 即可。
这就是一个比较简单的泛化物品背包问题,甚至不需要合并操作。
我们考虑两个食材 \(x\) 和 \(y\),在它们之前已经花费了 \(t\) 的时间,那么此时如果先将 \(x\) 食材做成菜再做 \(y\),此时的价值为 \(a_x - (t + c_x) \times b_x + a_y - (t + c_x + c_y) \times b_y\);那么此时如果先将 \(y\) 食材做成菜再做 \(x\),此时的价值为 \(a_y - (t + c_y) \times b_y + a_x - (t + c_y + c_x) \times b_x\)。我们假设第一种顺序的价值比第二种大,那么将两式一减,可以得到 \(c_x \times b_y < c_y \times b_x\),此时我们只需要拍一遍序,再做一遍 01 背包即可。这也是泛化物品背包的另一种解法,那就是考虑顺序后再 01 背包。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 9;
struct Ingredient{
int a, b, c;
} p[N];
int dp[N], n, m, ans;
bool cmp(Ingredient x, Ingredient y) {
return x.c * y.b < y.c * x.b;
}
signed main(){
scanf("%lld%lld", &m, &n);
for(int i = 1; i <= n; i++)
scanf("%d", &p[i].a);
for(int i = 1; i <= n; i++)
scanf("%d", &p[i].b);
for(int i = 1; i <= n; i++)
scanf("%d", &p[i].c);
sort(p + 1, p + n + 1, cmp);
for(int i = 1; i <= n; i++)
for(int j = m; j >= p[i].c; j--)
dp[j] = max(dp[j], dp[j - p[i].c] + p[i].a - j * p[i].b);
for(int i = 1; i <= m; i++)
ans = max(ans, dp[i]);
printf("%lld", ans);
return 0;
}
背包方案与计数
输出任意最优方案
对于 01 背包的函数 \(dp_{i, j}\),我们再记录一个 \(f_{i, j} = 0 / 1\) 表示 \(dp_{i, j}\) 是从 \(dp_{i - 1, j}\) 转移而来还是从 \(dp_{i - 1, j - w_i}\) 转移而来,找寻方案的时候只用从 \(dp_{n, m}\) 倒着不断往回找是从哪个状态转移过来就可以了。
其实,也可以不存 \(f_{i, j}\),此时外层循环我们需要从 \(n\) 往 \(1\) 枚举,这样我们就知道每个状态是由哪个状态转移而来,然后我们再从 \(1\) 到 \(n\) 正序统计答案,此时如果 \(dp_{i, j} = dp_{i + 1, j - w_i}\),那么说明可以选择第 \(i\) 个物品,将第 \(i\) 个物品加入答案即可。注意费用不要超过限制。
输出字典序最小的最优方案
一个 01 背包问题可能会有多组物品,每组都可以作为答案,现在我们要求出所有组物品中排序好后字典序最小的哪一个。
我们考虑到最优的情况一定是 \(1, 2, 3, \dots\),这启示我们在转移的时候,如果 \(f_{i, j} = f_{i + 1, j - w_i} + v_i\),那么我们应该选取后者来转移,这样可以尽可能选编号小的点来转移。其它的就和输出任意最优方案一样了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 9;
int dp[N][N], w[N], v[N], n, m;
vector <int> vec;
signed main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%d%d", &w[i], &v[i]);
for(int i = n; i >= 1; i--){
for(int j = 0; j <= m; j++){
if(j < w[i])
dp[i][j] = dp[i + 1][j];
else
dp[i][j] = max(dp[i + 1][j], dp[i + 1][j - w[i]] + v[i]);
}
}
for(int i = 1, j = m; i <= n; i++){
if(j >= w[i] && dp[i][j] == dp[i + 1][j - w[i]] + v[i]){
vec.push_back(i);
j -= w[i];
}
}
for(int i : vec)
printf("%d ", i);
return 0;
}
求第 \(k\) 优方案
真是太神秘了,生活中应该没有人去求第 \(k\) 优解吧?
还是以 \(01\) 背包为例,我们这次不止把最优解记录在 \(dp_{i, j}\) 里,我们将前 \(k\) 优解全部记录下来,相当于每个 \(dp_{i, j}\) 是一个大小为 \(k\) 的优先队列。而每次转移的时候,我们需要将 \(dp_{i - 1, j}\) 和 \(dp_{i - 1, j - w_i} + v_i\) 这两个堆合并起来,并且取前 \(k\) 大的值保留下来。此时我们在时间和空间复杂度上都多了一个 \(k\)。
其实对于几乎所有求第 \(k\) 大值的问题(比如 \(k\) 短路),我们都可以将原先的 DP 函数看成一个堆,转移时就是堆和堆的合并。在 \(k\) 比较小的时候我们可以直接暴力插入,在 \(k\) 比较大的时候(比如 洛谷 P2483 【模板】k 短路 / [SDOI2010] 魔法猪学院),我们就需要用到可持久化可并堆这一科技了,不过这和 DP 已经没有什么关系了,也就不在这里赘述了。
另外还要注意题目对于第 \(k\) 优解的定义,将策略不同但权值相同的两个方案是看作同一个解还是不同的解。如果是前者,则维护优先队列时要保证队列里的数没有重复的。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 9, M = 1e3 + 9, K = 39;
int dp[M][K], w[N], v[N], tmp[K], n, m, k, T;
int main(){
scanf("%d", &T);
while(T--){
scanf("%d%d%d", &n, &m, &k);
for(int i = 1; i <= n; i++)
scanf("%d", &v[i]);
for(int i = 1; i <= n; i++)
scanf("%d", &w[i]);
memset(dp, 0, sizeof(dp));
for(int i = 1; i <= n; i++){
for(int j = m; j >= w[i]; j--){
int c1 = 1, c2 = 1, cnt = 1;
while(cnt <= k && c1 <= k && c2 <= k){
if(dp[j][c1] > dp[j - w[i]][c2] + v[i])
tmp[cnt] = dp[j][c1++];
else
tmp[cnt] = dp[j - w[i]][c2++] + v[i];
if(tmp[cnt] != tmp[cnt - 1])
cnt++;
}
while(cnt <= k && c1 <= k){
tmp[cnt] = dp[j][c1++];
if(tmp[cnt] != tmp[cnt - 1])
cnt++;
}
while(cnt <= k && c2 <= k){
tmp[cnt] = dp[j - w[i]][c2++] + v[i];
if(tmp[cnt] != tmp[cnt - 1])
cnt++;
}
for(int l = 1; l <= k; l++)
dp[j][l] = tmp[l];
}
}
printf("%d\n", dp[m][k]);
}
return 0;
}
输出方案数
此时我们就不用考虑是否是最优解了,而需要统计装满背包的所有方案。
如果 \(n\) 比较小,那么我们可以仿照之前的 DP 转移方程,只是把 \(\max\) 改成 \(+\),因此转移方程就变成了 \(cnt_{i, j} = cnt_{i - 1, j} + cnt_{i - 1, j - w_i}\),初始 \(cnt_{0, 0} = 1\)。那么最终答案就是 \(\displaystyle\sum_{i = 1}^n cnt_{i, m}\)。
对于 \(n\) 更大的求方案数的题目,需要用到生成函数,详见组合数学学习笔记(三):生成函数 1(OGF)。
输出最优方案数
结合求方案总数和求最优方案,我们只需要最后输出 \(cnt_{n, m}\) 即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 9, M = 1e3 + 9, MOD = 1e9 + 7;
int dp[M], cnt[M], w[N], v[N], n, m;
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%d%d", &w[i], &v[i]);
for(int i = 0; i <= m; i++)
cnt[i] = 1;
for(int i = 1; i <= n; i++)
for(int j = m; j >= w[i]; j--){
if(dp[j - w[i]] + v[i] > dp[j]){
dp[j] = dp[j - w[i]] + v[i];
cnt[j] = cnt[j - w[i]];
} else if(dp[j - w[i]] + v[i] == dp[j])
cnt[j] = (cnt[j - w[i]] + cnt[j]) % MOD;
}
printf("%d", cnt[m]);
return 0;
}
背包合并
背包增减
背包 DP 难题
洛谷 P3188 [HNOI2007] 梦幻岛宝珠
LOJ6089 小 Y 的背包计数问题
非常有启发性的一道题目。
由于所有数字的和一定,因此我们考虑根号分治,最后两部分做一个卷积即可。对于重量小于 \(\sqrt n\) 的物品,直接暴力跑多重背包,时间复杂度为 \(\mathcal O(\sqrt n^3) = \mathcal O(n \sqrt n)\)。
现在考虑重量大于 \(\sqrt n\) 的物品,我们发扬人类智慧,将原先往背包中放物品的操作,拆分成一下两种操作:
-
往背包中加入一个重量为 \(\sqrt n\) 的物品;
-
让背包中所有物品的重量增加 \(1\)。
可以发现这样可以生成所有可能的物品序列。
那么这样做有什么好处呢?此时我们就可以设计出另外一种 DP 方式了。我们设 \(dp_{i, j}\) 表示放了 \(i\) 个物品,总重量为 \(j\) 的方案数。我们考虑上一次操作是第一种还是第二种。如果是第一种,那么 \(dp_{i, j}\) 就可以从 \(dp_{i - 1, j - \sqrt n}\) 转移而来,否则就可以从 \(dp_{i, j - i}\) 转移而来。因此 \(dp_{i, j} = dp_{i - 1, j - \sqrt n} + dp_{i, j - i}\),此时我们发现 \(i\) 不会超过 \(\sqrt n\),而 \(j\) 不会超过 \(n\),那么这一部分的时间复杂度就是 \(\mathcal O(n \sqrt n)\)。因此总时间复杂度就是 \(\mathcal O(n \sqrt n)\) 的。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 9, B = 4e2 + 9, MOD = 23333333;
int dp[N], dp2[B][N], sum[N], sum2[N], n, ans, len;
signed main(){
scanf("%lld", &n);
dp[0] = sum[0] = 1;
len = sqrt(n) + 2;
for(int i = 1; i < len; i++){
for(int j = 1; j <= n; j++){
if(j >= i)
sum[j] = (sum[j - i] + dp[j]) % MOD;
else
sum[j] = dp[j];
if(j >= i * (i + 1))
dp[j] = (sum[j] - sum[j - i * (i + 1)] + MOD) % MOD;
else
dp[j] = sum[j];
}
}
dp2[0][0] = sum2[0] = 1;
for(int i = 1; i <= n / len; i++)
for(int j = i * len; j <= n; j++){
dp2[i][j] = (dp2[i - 1][j - len] + dp2[i][j - i]) % MOD;
sum2[j] = (sum2[j] + dp2[i][j]) % MOD;
}
for(int i = 0; i <= n; i++)
ans = (ans + dp[i] * sum2[n - i]) % MOD;
printf("%lld", ans);
return 0;
}
洛谷 P6453 [COCI 2008/2009 #4] PERIODNI
线性 DP
子序列问题
方格取数问题
区间 DP
状压 DP
普通状压 DP
P1879 [USACO06NOV] Corn Fields G
轮廓线 DP
数位 DP
树形 DP
普通树形 DP
换根 DP
参考资料
- 算法竞赛 罗勇军、郭卫斌
本文来自博客园,作者:Orange_new,转载请注明原文链接:https://www.cnblogs.com/JPGOJCZX/p/18422813


 浙公网安备 33010602011771号
浙公网安备 33010602011771号